Teil B
1
Abbildung 1 zeigt den Graphen  einer ganzrationalen Funktion
einer ganzrationalen Funktion  dritten Grades mit Definitionsmenge
dritten Grades mit Definitionsmenge 
 schneidet die
schneidet die  -Achse bei
-Achse bei  und
und  und verläuft durch den Punkt
und verläuft durch den Punkt 
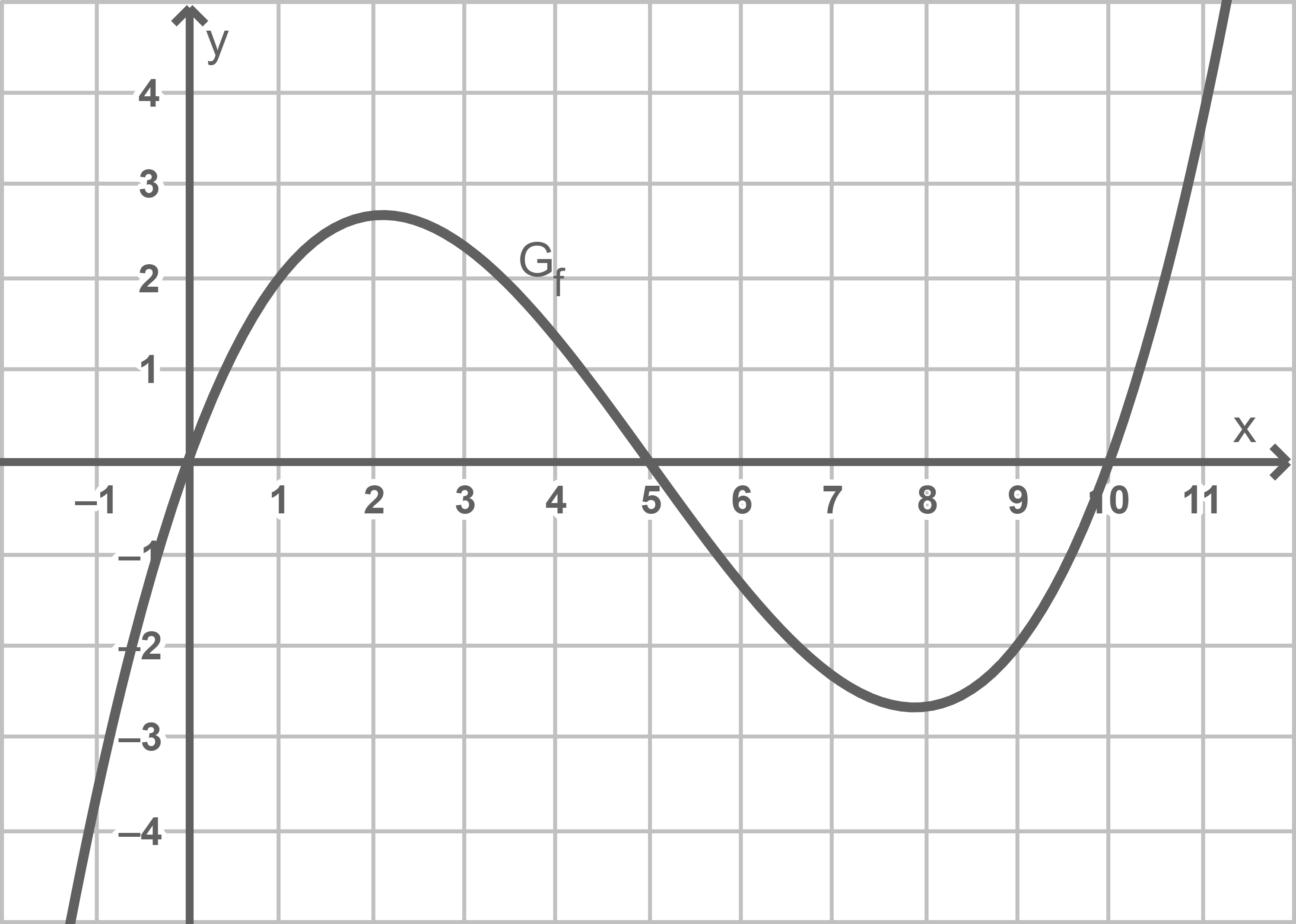
Abb. 1
a)
Ermittle einen Funktionsterm von 
(zur Kontrolle:  )
)
(4 BE)
b)
Zeige, dass  im Punkt
im Punkt  einen Wendepunkt besitzt, und ermittle eine Gleichung der Tangente an
einen Wendepunkt besitzt, und ermittle eine Gleichung der Tangente an  im Punkt
im Punkt 
(6 BE)
c)
(4 BE)
d)
(3 BE)
e)
Begründe mithilfe von Abbildung 1, dass  mindestens eine weitere positive Nullstelle hat.
mindestens eine weitere positive Nullstelle hat.
(2 BE)
f)
Begründe, dass  höchstens vier Nullstellen hat.
höchstens vier Nullstellen hat.
(2 BE)
g)
Für  gilt, dass der Graph von
gilt, dass der Graph von  und der Graph einer trigonometrischen Funktion
und der Graph einer trigonometrischen Funktion 

- die gleichen Schnittpunkte mit der
-Achse besitzen,
- beide nicht unterhalb der
-Achse verlaufen,
- jeweils mit der
-Achse eine Fläche des Inhalts
einschließen.
(6 BE)
2
Die Kosten, die einem Unternehmen bei der Herstellung einer Flüssigkeit entstehen, können durch die Funktion  mit
mit ![\(x \in[0 ; 9]\)](https://www.schullv.de/resources/formulas/ca784a03972acd82b8448deb8af966f7b1753bffa3260c96cb05e21c98e9b3a3_light.svg) beschrieben werden. Dabei gibt
beschrieben werden. Dabei gibt  die Kosten in 1000 Euro an, die bei der Produktion von
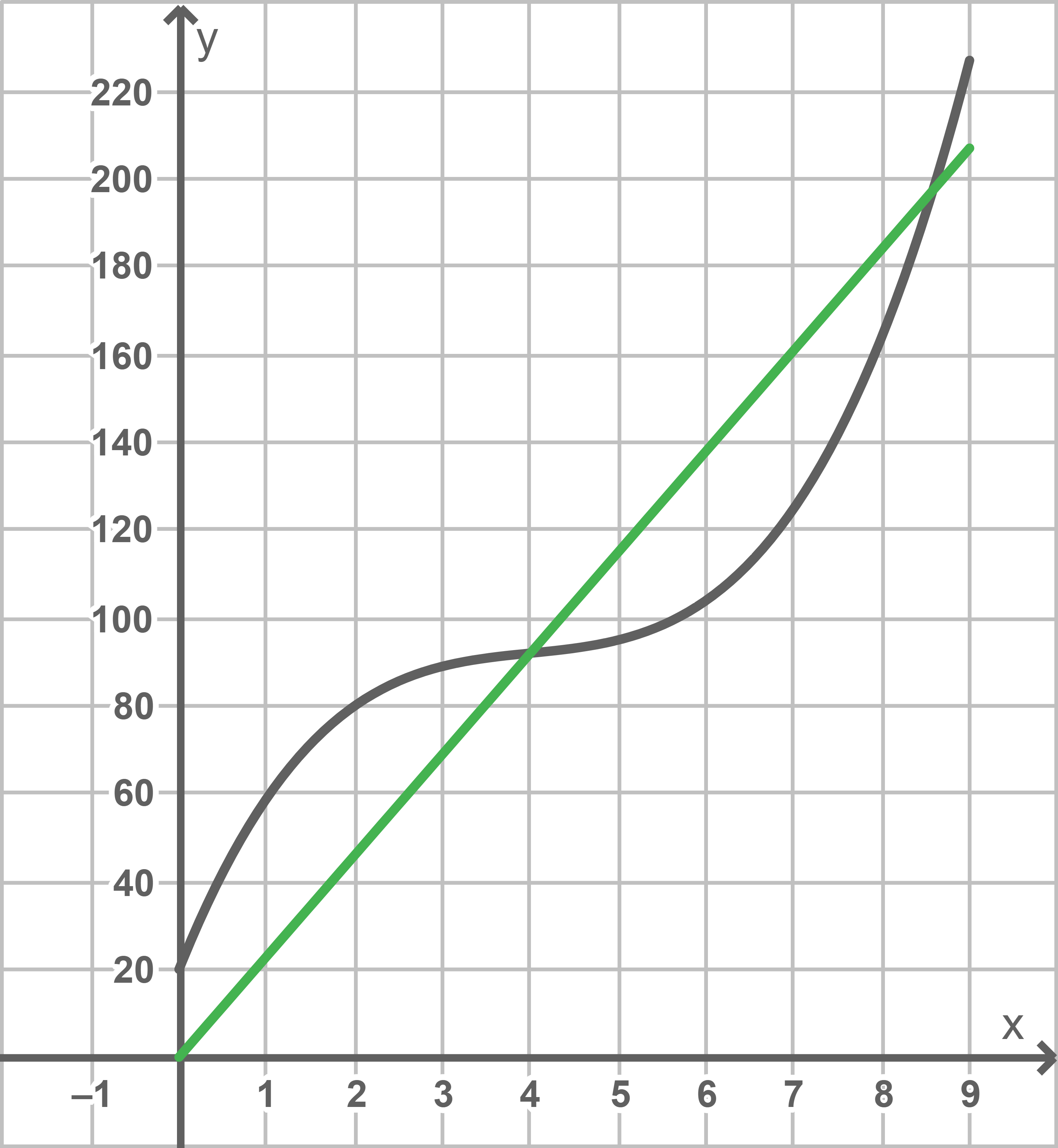
die Kosten in 1000 Euro an, die bei der Produktion von  Kubikmetern der Flüssigkeit insgesamt entstehen. Abbildung 2 zeigt den Graphen von
Kubikmetern der Flüssigkeit insgesamt entstehen. Abbildung 2 zeigt den Graphen von 

 mit
mit  gibt für
gibt für  den Erlös (in 1000 Euro) an, den das Unternehmen beim Verkauf von
den Erlös (in 1000 Euro) an, den das Unternehmen beim Verkauf von  Kubikmetern der Flüssigkeit erzielt. Für die sogenannte Gewinnfunktion
Kubikmetern der Flüssigkeit erzielt. Für die sogenannte Gewinnfunktion  gilt
gilt  . Positive Werte von
. Positive Werte von  werden als Gewinn bezeichnet, negative als Verlust.
werden als Gewinn bezeichnet, negative als Verlust.

Abb. 2
a)
Gib mithilfe von Abbildung 2


Die Funktion
die Produktionsmenge an, bei der die Kosten  Euro betragen.
Euro betragen.
das Monotonieverhalten von  an und deute deine Angabe im Sachzusammenhang.
an und deute deine Angabe im Sachzusammenhang.
(3 BE)
b)
Zeige, dass das Unternehmen keinen Gewinn erzielt, wenn vier Kubikmeter der Flüssigkeit verkauft werden.
(2 BE)
c)
Zeichne den Graphen von  in Abbildung 2 ein. Bestimme mithilfe der so entstehenden Darstellung den Bereich, in dem die verkaufte Menge der Flüssigkeit liegen muss, damit das Unternehmen einen Gewinn erzielt.
in Abbildung 2 ein. Bestimme mithilfe der so entstehenden Darstellung den Bereich, in dem die verkaufte Menge der Flüssigkeit liegen muss, damit das Unternehmen einen Gewinn erzielt.
(3 BE)
d)
Berechne, welche Menge der Flüssigkeit verkauft werden muss, damit das Unternehmen den größten Gewinn erzielt.
(5 BE)
(40 BE)
1
a)
Da  eine ganzrationale Funktion dritten Grades ist, hat ihr Funktionsterm die allgemeine Form
eine ganzrationale Funktion dritten Grades ist, hat ihr Funktionsterm die allgemeine Form  Die Aufgabenstellung liefert folgende Eigenschaften von
Die Aufgabenstellung liefert folgende Eigenschaften von 
 Einsetzen in die anderen drei Gleichungen liefert:
Einsetzen in die anderen drei Gleichungen liefert:
 Umstellen von Gleichung
Umstellen von Gleichung  nach
nach  liefert
liefert  Einsetzen in die anderen beiden Gleichungen liefert folgendes Gleichungssystem:
Umstellen von Gleichung
Einsetzen in die anderen beiden Gleichungen liefert folgendes Gleichungssystem:
Umstellen von Gleichung  nach
nach  ergibt:
Einsetzen in
ergibt:
Einsetzen in  liefert:
Einsetzen von
liefert:
Einsetzen von  in die Darstellungen von
in die Darstellungen von  und
und  liefert weiter:
liefert weiter:
![\(\begin{array}[t]{rll}
b&=& -6\cdot \dfrac{1}{18} -\dfrac{1}{2}\\[5pt]
&=& -\dfrac{5}{6} \\[10pt]
c&=& 2-a-b \\[5pt]
&=& 2-\dfrac{1}{18}-\left(-\dfrac{5}{6} \right) \\[5pt]
&=& \dfrac{25}{9} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/5e6854a368d0dc1105a216fbbb3e360da1167d1a0382ac0af9a6c9d46928bac1_light.svg) Ein Funktionsterm von
Ein Funktionsterm von  lautet somit:
lautet somit:
![\(\begin{array}[t]{rll}
f(x)&=& \dfrac{1}{18} x^3 -\dfrac{5}{6}x^2 + \dfrac{25}{9}x\\[5pt]
&=& \dfrac{1}{18}\cdot(x^3-15x^2+50x)
\end{array}\)](https://www.schullv.de/resources/formulas/1d5d88414d2b2f7dc1a8f0dcd226b8e6d25e13def7f3a248368217f8413aff73_light.svg)
b)
Wendepunkt zeigen
Für die ersten drei Ableitungen von  folgt:
folgt:
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/83c1832f21d505c3fb482ad2e7e3b86190548e1b275afc589d5a6df8e9009969_light.svg) 1. Schritt: Notwendiges Kriterium für Wendestellen überprüfen
1. Schritt: Notwendiges Kriterium für Wendestellen überprüfen
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/3c2293bf13010117192b9ffcef30340b5e6ab22a27c56d8e227ef490fe3610fd_light.svg) 2. Schritt: Hinreichendes Kriterium für Wendestellen überprüfen
2. Schritt: Hinreichendes Kriterium für Wendestellen überprüfen
 Das sowohl das notwendige als auch das hinreichende Kriterium für Wendestellen für
Das sowohl das notwendige als auch das hinreichende Kriterium für Wendestellen für  erfüllt ist und aus der Aufgabenstellung
erfüllt ist und aus der Aufgabenstellung  folgt, besitzt
folgt, besitzt  im Punkt mit den Koordinaten
im Punkt mit den Koordinaten  einen Wendepunkt.
Tangentengleichung ermitteln
Für die Steigung
einen Wendepunkt.
Tangentengleichung ermitteln
Für die Steigung  der gesuchten Tangente folgt:
der gesuchten Tangente folgt:
![\(\begin{array}[t]{rll}
m&=& f](https://www.schullv.de/resources/formulas/f609670de6a50f356f053e3d8967eefaf004940306660347b60c87bf21992dbd_light.svg) Einsetzen der Koordinaten von
Einsetzen der Koordinaten von  in
in  liefert für
liefert für 
![\(\begin{array}[t]{rll}
0&=& -\dfrac{25}{18}\cdot 5 +b \\[5pt]
0&=& -\dfrac{125}{18}+b &\quad \scriptsize \mid\;+\frac{125}{18} \\[5pt]
\dfrac{125}{18}&=& b
\end{array}\)](https://www.schullv.de/resources/formulas/3d1f88b41a3dbe1f299f8ef12721d9bea83c90f9f10eef910966bd307a108d2e_light.svg) Eine Gleichung der Tangente an
Eine Gleichung der Tangente an  im Punkt
im Punkt  ist somit gegeben durch
ist somit gegeben durch 
c)
Verschiebung ermitteln
Der Funktionsterm von  lässt sich mit Hilfe der dritten binomischen Formel wie folgt umformen:
lässt sich mit Hilfe der dritten binomischen Formel wie folgt umformen:
![\(\begin{array}[t]{rll}
g(x)&=& \dfrac{1}{18} \cdot \left(x^3-25x\right) \\[5pt]
&=& \dfrac{1}{18}x\cdot \left(x^2-25\right) \\[5pt]
&=& \dfrac{1}{18}x\cdot \left(x-5\right)\cdot \left(x+5\right)
\end{array}\)](https://www.schullv.de/resources/formulas/f3a6ba475b6e289c112a0c76b70f092a4f96aba11f2862107404e98f17e736d4_light.svg) Aus dem Satz vom Nullprodukt folgt somit, dass die Nullstellen von
Aus dem Satz vom Nullprodukt folgt somit, dass die Nullstellen von  durch
durch  und
und  gegeben sind. Da die Nullstellen von
gegeben sind. Da die Nullstellen von  durch
durch  und
und  gegeben sind, muss der Graph von
gegeben sind, muss der Graph von  um fünf Einheiten in positive
um fünf Einheiten in positive  -Richtung verschoben werden.
Symmetrie begründen
Da im Funktionsterm von
-Richtung verschoben werden.
Symmetrie begründen
Da im Funktionsterm von  die Variable
die Variable  nur mit ungeraden Exponenten vorkommt, ist der Graph von
nur mit ungeraden Exponenten vorkommt, ist der Graph von  punktsymmetrisch zum Koordinatenursprung. Da
punktsymmetrisch zum Koordinatenursprung. Da  aus
aus  durch Verschiebung um fünf Einheiten in positive
durch Verschiebung um fünf Einheiten in positive  -Richtung hervorgeht und seinen Wendepunkt im Punkt mit den Koordinaten
-Richtung hervorgeht und seinen Wendepunkt im Punkt mit den Koordinaten  besitzt, ist
besitzt, ist  somit punktsymmetrisch bezüglich diesem.
somit punktsymmetrisch bezüglich diesem.
d)
Die Funktion  beschreibt die Flächenbilanz der Fläche, die der Graph von
beschreibt die Flächenbilanz der Fläche, die der Graph von  mit der
mit der  -Achse zwischen
-Achse zwischen  und einem allgemeinen
und einem allgemeinen  einschließt.
einschließt.
Für gilt
gilt  da die beiden Integrationsgrenzen übereinstimmen.
da die beiden Integrationsgrenzen übereinstimmen.
Nach Aufgabenteil c) ist punktsymmetrisch bezüglich seines Wendepunkts mit den Koordinaten
punktsymmetrisch bezüglich seines Wendepunkts mit den Koordinaten  Der Inhalt der Fläche, die
Der Inhalt der Fläche, die  zusammen mit der
zusammen mit der  -Achse zwischen
-Achse zwischen  und
und  einschließt, ist somit gleich dem Inhalt der Fläche, die zwischen
einschließt, ist somit gleich dem Inhalt der Fläche, die zwischen  und
und  eingeschlossen wird. Da die eine Fläche oberhalb und die andere unterhalb der
eingeschlossen wird. Da die eine Fläche oberhalb und die andere unterhalb der  -Achse liegt, nimmt
-Achse liegt, nimmt  auch an der Stelle
auch an der Stelle  den Wert Null an.
den Wert Null an.
Für
Nach Aufgabenteil c) ist
e)
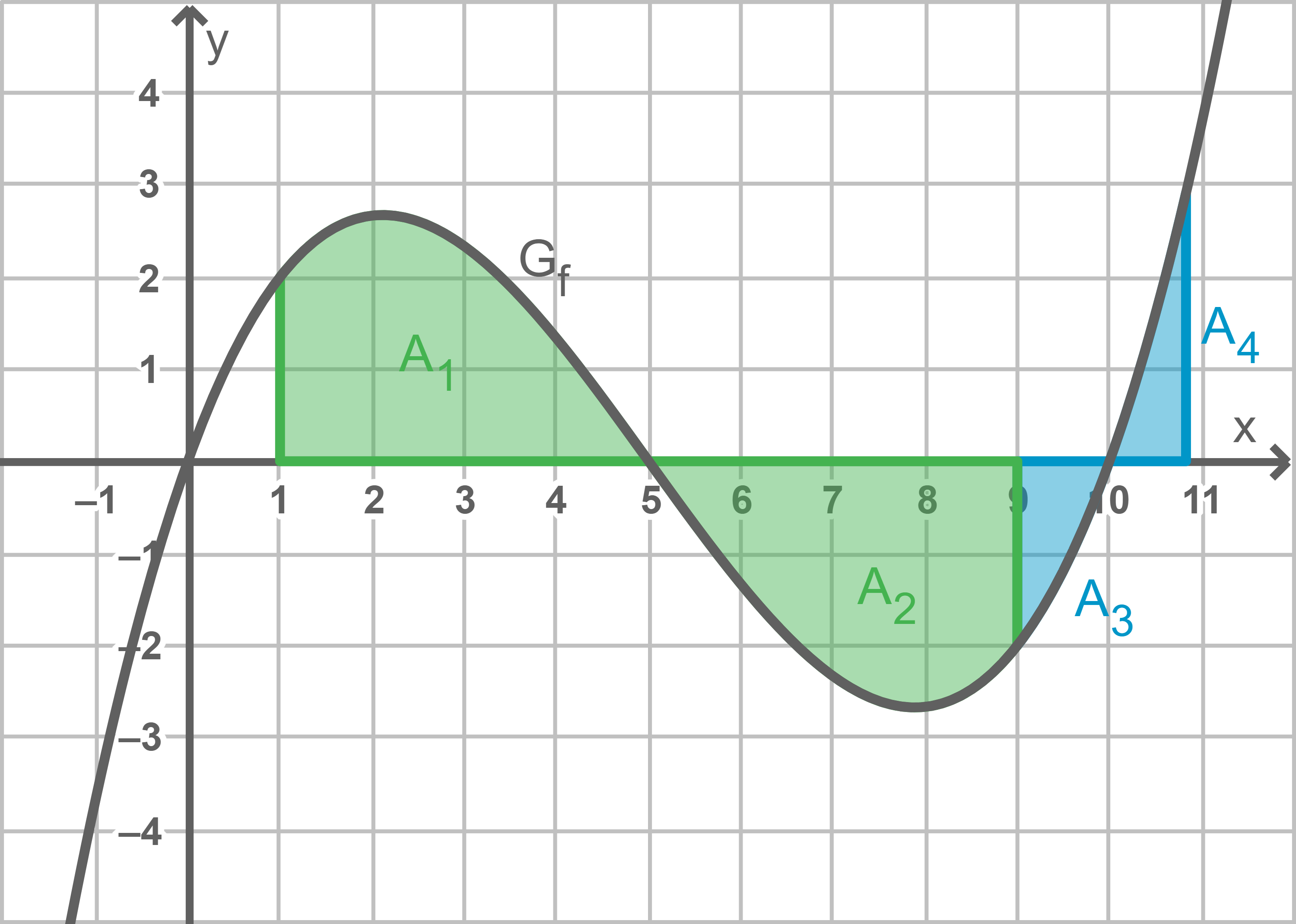
Da  bei
bei  erneut die
erneut die  -Achse schneidet, gibt es analog zu den eingezeichneten Flächen
-Achse schneidet, gibt es analog zu den eingezeichneten Flächen  und
und  deren Beitrag zum Wert von
deren Beitrag zum Wert von  sich gegenseitig aufheben, zwei weitere gleichgroße Flächen
sich gegenseitig aufheben, zwei weitere gleichgroße Flächen  und
und  die wie in der Skizze angeordnet sind. Somit besitzt
die wie in der Skizze angeordnet sind. Somit besitzt  an einer Stelle
an einer Stelle  eine weitere Nullstelle.
eine weitere Nullstelle.
f)
Da  eine ganzrationale Funktion dritten Grades ist, ist die Integralfunktion
eine ganzrationale Funktion dritten Grades ist, ist die Integralfunktion  eine ganzrationale Funktion vierten Grades, welche höchstens vier Nullstellen besitzen.
eine ganzrationale Funktion vierten Grades, welche höchstens vier Nullstellen besitzen.
g)
Aus der Aufgabenstellung lassen sich folgende Bedingungen ableiten:
 am besten eine Sinusfunktion der folgenden allgemeinen Form:
am besten eine Sinusfunktion der folgenden allgemeinen Form:
 Damit
Damit  gilt, muss
gilt, muss  gelten. Somit ergibt sich
gelten. Somit ergibt sich  Da die nächste Nullstelle bei
Da die nächste Nullstelle bei  liegen soll, besitzt die Funktion
liegen soll, besitzt die Funktion  eine Periode von
eine Periode von  Für
Für  folgt damit
folgt damit 
Mit Hilfe der letzten Bedingung folgt nun für Eine möglicher Funktionsterm ist somit gegeben durch
Eine möglicher Funktionsterm ist somit gegeben durch 
für
Mit Hilfe der letzten Bedingung folgt nun für
2
a)
Die Kosten betragen bei einer Produktionsmenge von ca.  Kubikmetern der Flüssigkeit
Kubikmetern der Flüssigkeit  Euro.
Euro.
Die Abbildung liefert, dass  für
für  streng monoton steigt. Die Kosten steigen somit mit der Menge der produzierten Flüssigkeit.
streng monoton steigt. Die Kosten steigen somit mit der Menge der produzierten Flüssigkeit.
b)
Bei einem Verkauf von  Kubikmetern der Flüssigkeit beträgt der Gewinn
Kubikmetern der Flüssigkeit beträgt der Gewinn  Das Unternehmen erzielt in diesem Fall somit keinen Gewinn.
Das Unternehmen erzielt in diesem Fall somit keinen Gewinn.
c)
Das Unternehmen erzielt dann Gewinn, wenn der Erlös größer ist als die Kosten, das heißt wenn der in der Abbildung grün eingezeichnete Graph von  oberhalb des Graphen von
oberhalb des Graphen von  verläuft. Mit Hilfe der Abbildung folgt somit, dass die verkaufte Menge der Flüssigkeit im Bereich zwischen
verläuft. Mit Hilfe der Abbildung folgt somit, dass die verkaufte Menge der Flüssigkeit im Bereich zwischen  und
und  Kubikmetern liegen muss, damit das Unternehmen einen Gewinn erzielt.
Kubikmetern liegen muss, damit das Unternehmen einen Gewinn erzielt.
d)
Für die ersten beiden Ableitungen der Gewinnfunktion  folgt:
folgt:
![\(\begin{array}[t]{rll}
G](https://www.schullv.de/resources/formulas/2aae3e11c7d7994c3407edb93b207490ec75269823c647da3b82168edc2b5e22_light.svg) 1. Schritt: Notwendiges Kriterium für Extremstellen anwenden
1. Schritt: Notwendiges Kriterium für Extremstellen anwenden
![\(\begin{array}[t]{rll}
G](https://www.schullv.de/resources/formulas/a03440111b991609aadc1f26d6fb777f0751d5ae0fd86c7b7eeb3c40dcc7cff8_light.svg) Mit der
Mit der  -Formel folgt:
2. Schritt: Hinreichendes Kriterium für Extremstellen überprüfen
-Formel folgt:
2. Schritt: Hinreichendes Kriterium für Extremstellen überprüfen
![\(\begin{array}[t]{rll}
G](https://www.schullv.de/resources/formulas/756550a14caef37287e21e0569a5691c521f0e80f0cab0ce1f904f08ad67c39a_light.svg) An der Stelle
An der Stelle  besitzt der Graph von
besitzt der Graph von  somit seinen einzigen Hochpunkt. Da aus der Abbildung aus Aufgabenteil 2c) entnommen werden kann, dass die Funktionswerte von
somit seinen einzigen Hochpunkt. Da aus der Abbildung aus Aufgabenteil 2c) entnommen werden kann, dass die Funktionswerte von  an den Intervallrändern negativ sind, ist der Gewinn an der Stelle
an den Intervallrändern negativ sind, ist der Gewinn an der Stelle  tatsächlich maximal. Es müssen somit
tatsächlich maximal. Es müssen somit  Kubikmeter der Flüssigkeit verkauft werden, damit das Unternehmen den größten Gewinn erzielt.
Kubikmeter der Flüssigkeit verkauft werden, damit das Unternehmen den größten Gewinn erzielt.