Teil B

Eine Seilbahn an einem Berg führt im unteren Abschnitt von der Talstation bis zu einer Seilstütze, im anschließenden oberen Abschnitt von der Seilstütze bis zur Bergstation. Der untere Abschnitt erstreckt sich $1000\;\text{m}$ in horizontaler Richtung, der obere Abschnitt $3000\;\text{m}.$
Abbildung 1 zeigt schematisch den Verlauf des Tragseils der Seilbahn sowie den darunter liegenden Querschnitt des Bergs. Im verwendeten Koordinatensystem ist $x$ die horizontale Entfernung von der Talstation in Kilometern und $y$ die Höhe über dem Meeresspiegel in Kilometern.

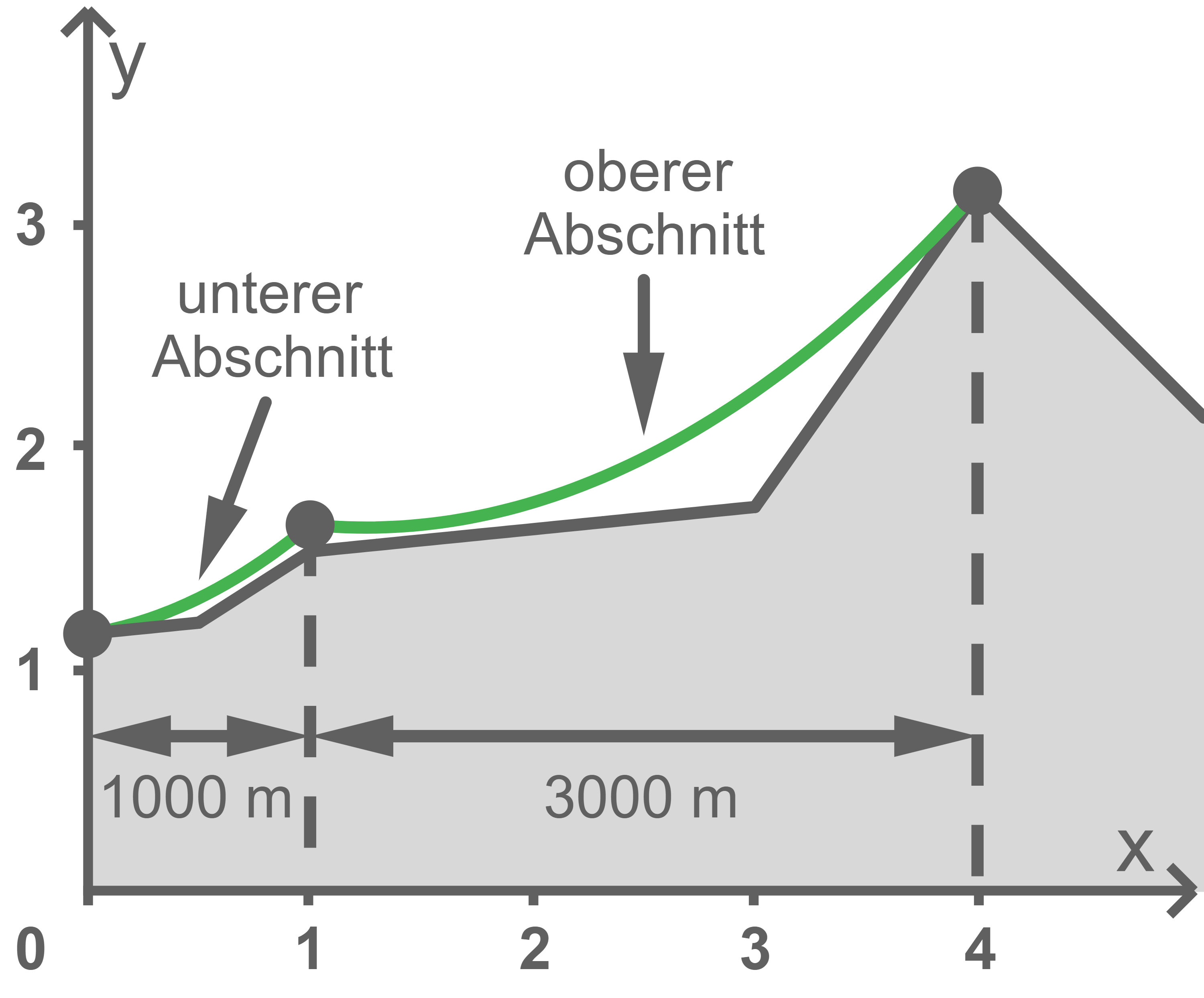
Diagramm mit einer grünen Kurve, die zwei Abschnitte und eine y-x-Achse zeigt. Beschriftungen für untere und obere Abschnitte.

Abb. 1

Im unteren Abschnitt, d.h. für $0 \leq x \leq 1,$ wird der Seilverlauf durch die in $\mathbb{R}$ definierte Funktion $f: x \mapsto 0,34 x^2+0,15 x+1,16$ beschrieben.

Bestimme den Höhenunterschied, den eine Kabine der Seilbahn auf dem unteren Abschnitt überwindet.

(2 BE)

Berechne die Größe des Winkels, unter dem das Seil im unteren Abschnitt auf die vertikal stehende Seilstütze trifft.

(3 BE)

Im oberen Abschnitt, d. h. für $1 \leq x \leq 4,$ wird der Seilverlauf durch die in $\mathbb{R}$ definierte Funktion $g: x \mapsto a x^2+b x+c$ mit $a, b, c \in \mathbb{R}$ beschrieben.
Die maximale Steigung des Seilverlaufs im oberen Abschnitt beträgt $110\,\%.$ Das Seil ist in der Bergstation in einer Höhe von $3150\,\text{m}$ über dem Meeresspiegel aufgehängt.

Bestimme die Werte von $a, b$ und $c.$

(zur Kontrolle: $a=0,2;b=-0,5;c=1,95$ )

(4 BE)

Ermittle die mittlere Steigung des Seilverlaufs im oberen Abschnitt.

(2 BE)

Berechne die horizontale Entfernung von der Seilstütze bis zu derjenigen Stelle im oberen Abschnitt des Seilverlaufs, an der die Steigung des Seilverlaufs $50\,\%$ beträgt.

(3 BE)

In einer Kabine der Seilbahn befindet sich ein Höhenmesser, der die aktuelle Höhe über dem Meeresspiegel misst. Begründe rechnerisch, dass sich im unteren Abschnitt der horizontale Abstand zur Talstation anhand der Höhe eindeutig bestimmen lässt, jedoch nicht im oberen Abschnitt.

(4 BE)

Die mittlere Geschwindigkeit der Kabine während der Fahrt zwischen Tal- und Bergstation beträgt 7 Meter pro Sekunde. Bestimme unter Verwendung des folgenden Hinweises die Dauer einer Fahrt von der Tal- bis zur Bergstation in Minuten.

$\;$

Hinweis: Ist ein Kurvenstück Graph einer in $\left[x_1 ; x_2\right]$ mit $x_1, x_2 \in \mathbb{R}$ definierten Funktion $r$ mit erster Ableitungsfunktion $\(r$ so gilt für die Länge $L$ dieses Kurvenstücks: $L=\displaystyle\int_{x_1}^{x_2}\sqrt{1+\left(r^{\prime}(x)\right)^2}\;\mathrm dx.$

(5 BE)

Das Hangprofil unterhalb der Seilbahn wird im Modell für den Bereich $1 \leq x \leq 3$ durch die in $\mathbb{R}$ definierte Funktion $h: x \mapsto 0,1 x+1,43$ beschrieben. Zu diesem Teil des Hangprofils weist das darüberliegende Seil an einer Stelle eine minimale Höhendifferenz auf.

Berechne diese minimale Höhendifferenz.

(3 BE)

Begründe geometrisch, dass diese minimale Höhendifferenz nicht gleich dem Abstand der betrachteten Position im Seilverlauf zum Hangprofil unterhalb der Seilbahn ist, und beschreibe, wie man diesen Abstand rechnerisch ermitteln kann.

(5 BE)

Gegeben ist die Schar der in $\mathbb{R}^+$ definierten Funktionen $s_k: x \mapsto \ln\left(\frac{k}{x}\right)$ mit $k \in \mathbb{R}^+.$

Begründe, dass jede Stammfunktion der in $\mathbb{R}^+$ definierten Funktion $v: x\mapsto -\frac{1}{x}$ eine der Funktionen $s_k$ ist.

(3 BE)

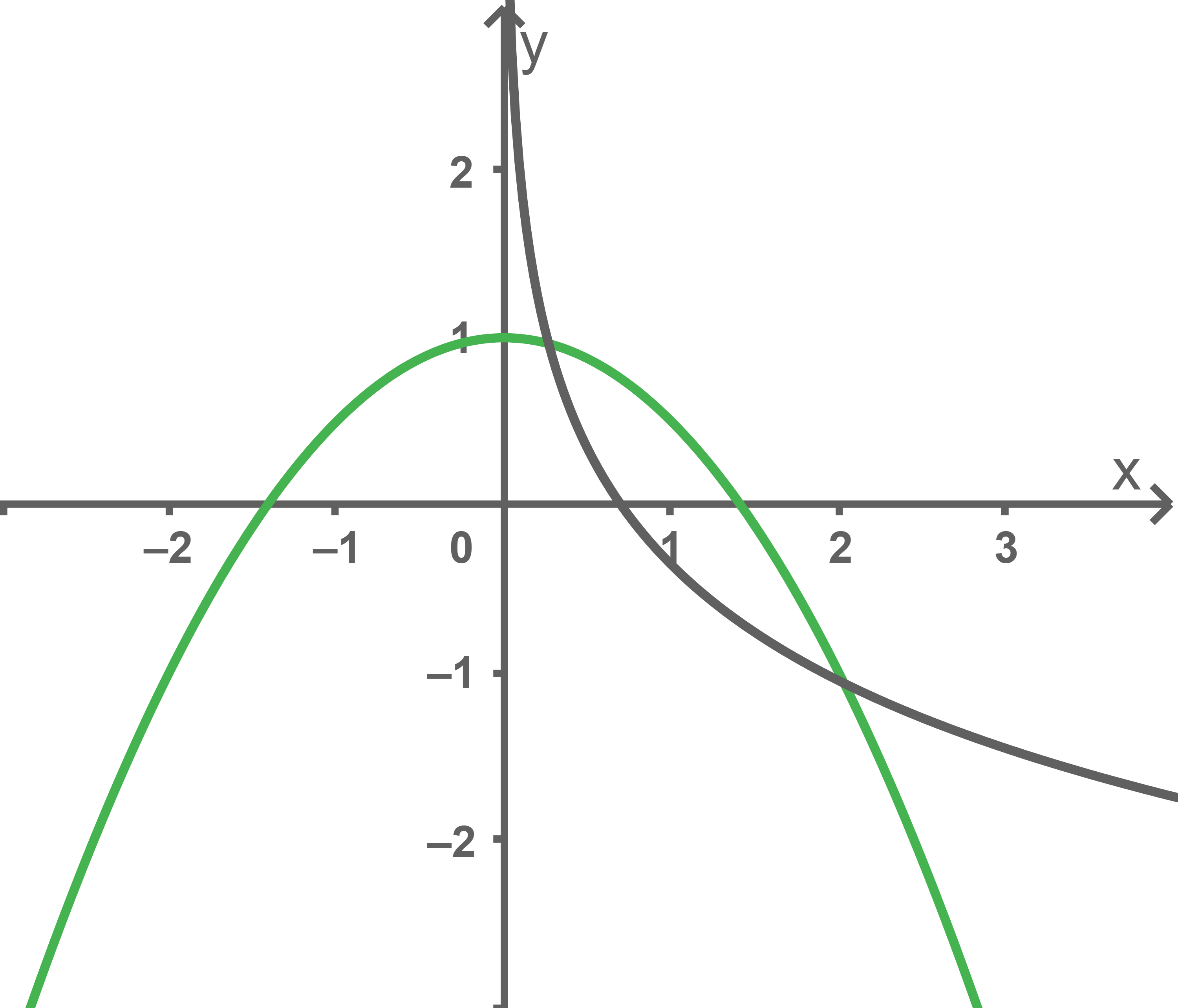
Abbildung 2 zeigt für einen bestimmten Wert von $k$ den Graphen von $s_k$ sowie den Graphen der in $\mathbb{R}$ definierten Funktion $p: x \mapsto-\frac{1}{2} x^2+1.$ Für diesen Wert von $k$ schneiden sich der Graph von $s_k$ und der Graph von $p$ in zwei Punkten, von denen einer die $x$ -Koordinate $0,25$ hat. Die Gerade durch diese beiden Schnittpunkte zerlegt das von den beiden Graphen eingeschlossene Flächenstück in zwei Teile.

Graph einer mathematischen Funktion mit einer grünen Kurve und Achsenbeschriftungen.

Abb. 2

Bestimme durch Rechnung näherungsweise das Verhältnis der Flächeninhalte dieser beiden Teile.

(zur Kontrolle: $k=0,25 \cdot \mathrm e^{\frac{31}{32}}$ )

(6 BE)

(40 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Rechenweg anzeigen

$f(1) - f(0) = 0,49$

Der Höhenunterschied im unteren Abschnitt beträgt somit $0,49\cdot1000 \;\text{m}=490\;\text{m}.$

Für die Ableitung von $f$ folgt mit dem CAS:

$\(f$

Somit folgt für die Steigung des Seils an der Seilstütze:

$\(\begin{array}[t]{rll} f$

Für den Winkel, den das Seil mit der Horizontalen einschließt, ergibt sich damit:

$\begin{array}[t]{rll} \tan(\alpha)&=&0,83 \\[5pt] \alpha&=&\tan^{-1}(0,83) \\[5pt] \alpha&\approx&39,69^\circ \end{array}$

Somit ergibt sich die Größe des Winkels, unter dem das Seil auf die vertikal stehende Seilstütze trifft, zu $90^\circ-39,69^\circ=60,31^\circ.$

Da der Seilverlauf im oberen Abschnitt durch eine quadratische Funktion beschrieben wird, folgt mit Hilfe der Abbildung, dass die maximale Steigung am rechten Randpunkt angenommen wird.

Aus den weiteren Angaben ergeben sich zusammen mit der in Teilaufgabe a) berechneten Höhe des Seils an der Seilstütze die folgenden Bedingungen:

$\(g$
$g(1) = 1,65$
$g(4) = 3,15$

Mit dem CAS ergibt sich die Ableitung zu $\(g$

Damit ergibt sich das folgende lineare Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&2a + b&=& 1,1 &\quad \\ \text{II}\quad&a + b + c&=& 1,65 &\quad \\ \text{II}\quad&16a + 4b + c&=&3,15 &\quad \\ \end{array}$

Lösen des Gleichungssystems mit dem CAS liefert $a=0,2, b=-0,5$ und $c=1,95.$

$\dfrac{g(4) - g(1)}{4 - 1} = \dfrac{3,15 - 1,65}{3} = 0,5$

Die mittlere Steigung des Seilverlaufs im oberen Abschnitt beträgt somit 500 Höhenmeter pro Kilometer.

Auflösen der Gleichung $\(g$ nach $x$ mit dem CAS liefert:

$x = 2,5$

Die horizontale Entfernung von der Seilstütze zu der beschriebenen Stelle beträgt somit $2,5\cdot1000 \;\text{m} -1000\;\text{m} =1500\;\text{m}.$

Der Verlauf der Seile wird in beiden Abschnitten durch eine quadratische Funktion beschrieben. Der horizontale Abstand zur Talstation lässt sich somit genau dann eindeutig bestimmen, wenn der betrachtete Teil der Funktion vollständig in einem der beiden Parabeläste liegt, das heißt der Scheitelpunkt außerhalb des betrachteten Bereichs ist.

Nullsetzen der Ableitungen von $f$ und $g$ liefert für die $x$ -Koordinaten der Scheitelpunkte:

$\(\begin{array}[t]{rll} f$

$\(\begin{array}[t]{rll} g$

Da der Scheitelpunkt von $f$ außerhalb des unteren Abschnitts liegt, der Scheitelpunkt von $g$ allerdings innerhalb des oberen Abschnitts, lässt sich im unteren Abschnitt der horizontale Abstand zur Talstation anhand der Höhe eindeutig bestimmen, im oberen Abschnitt jedoch nicht.

Für die Länge des Seils von der Tal- bis zur Bergstation gilt:

Rechenweg anzeigen

$L = \displaystyle\int_{0}^{1}\sqrt{1+\left(0,68x+0,15\right)^2}\;\mathrm dx$ $+ \displaystyle\int_{1}^{4}\sqrt{1+\left(0,4x-0,5\right)^2}\;\mathrm dx$

Lösen der Integrale mit dem CAS ergibt:

$L\approx4,61$

Die gesamte Seillänge beträgt somit ca. $4,61\cdot1000 \;\text{m} =4610\;\text{m}.$

Für die Dauer einer Fahrt gilt somit:

$t = \dfrac{4610 \;\text{m}}{7 \frac{\;\text{m}}{\;\text{s}}} = 658,57\;[\text{s}]$

Eine Fahrt von der Tal- bis zur Bergstation dauert somit ca. $\dfrac{658,57\,\text{s}}{60 \frac{\;\text{s}}{\;\text{min}}}\approx10,98 \;\text{min}.$

Für die ersten beiden Ableitungen der Differenzenfunktion folgt mit dem CAS:

$\(\begin{array}[t]{rll} g$

$\(g$

1. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} g$

Mit dem solve-Befehl des CAS folgt:

$x=1,5$

2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen

Da die zweite Ableitung konstant den Wert $0,4\gt0$ annimmt, besitzt die Differenzenfunktion an der Stelle $x=1,5$ einen Tiefpunkt.

Für die minimale Höhendifferenz folgt somit:

Rechenweg anzeigen

$g(1,5)-h(1,5) = 0,07$

Die minimale Höhendifferenz beträgt somit $0,07\cdot1000=70\;\text{m}.$

Während die minimale Höhendifferenz der Differenz entlang der Vertikalen gemessen wird und der Differenz der $y$ -Koordinaten an einem bestimmten $x$ -Wert entspricht (grau markierte Strecke), wird der kürzeste Abstand entlang derjenigen Gerade gemessen, die senkrecht zum Hang steht (blau markierte Strecke). Die minimale Höhendifferenz ist somit nicht gleich dem kürzesten Abstand zwischen dem Seil und dem Hangprofil.

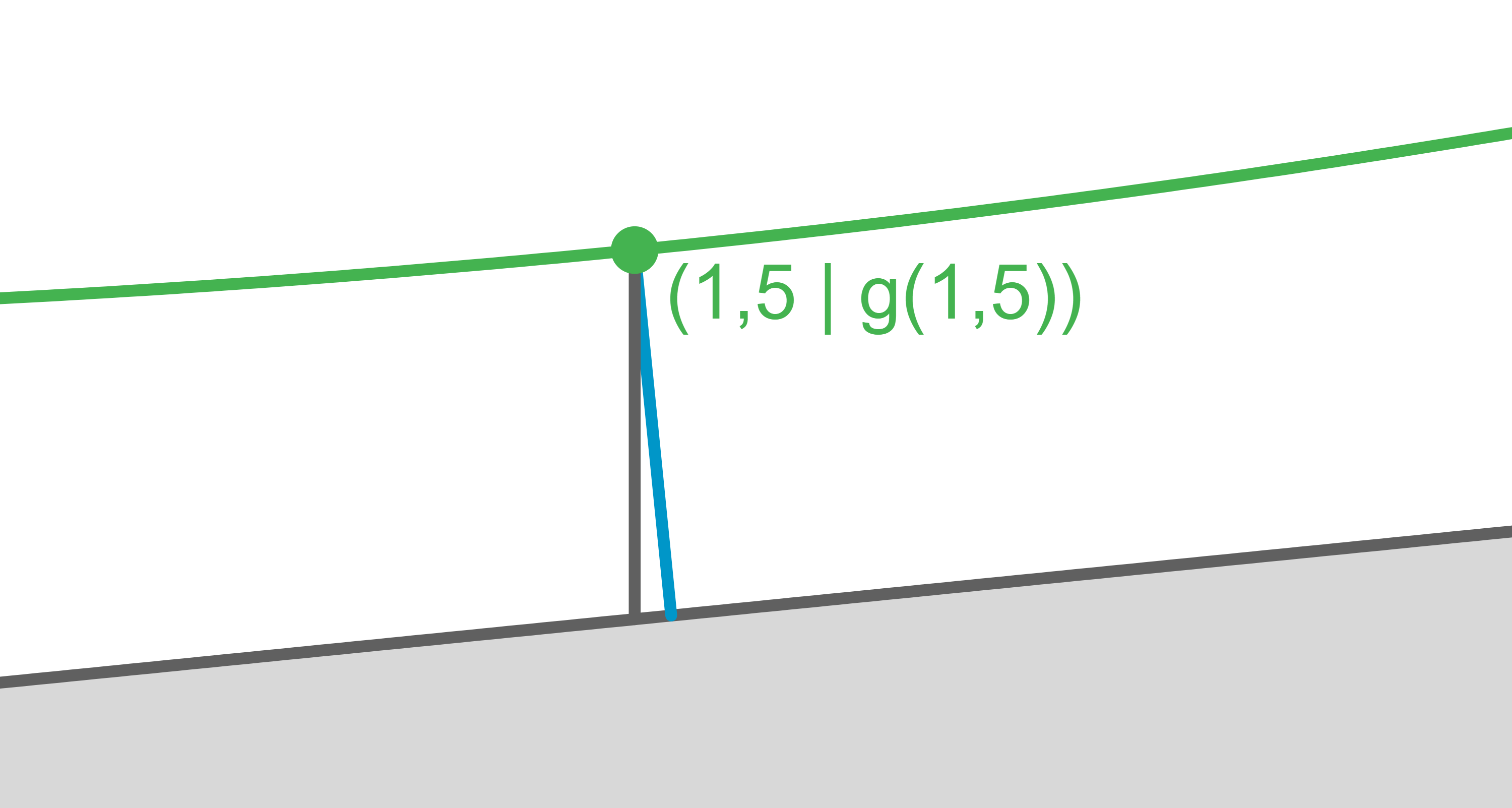Grafik mit einer Funktion und einem Punkt auf der Kurve, dargestellt mit Koordinaten und Linien.

Um den in blau dargestellten Abstand zu ermitteln, muss eine Gleichung der Geraden $s,$ auf der die Strecke liegt und die durch den betrachteten Punkt verläuft, aufgestellt werden.

Da die Gerade orthogonal zum Hang verlaufen soll, folgt mit der Steigung $m_h=0,1$ der Geraden $h:$

$m_s=-\dfrac{1}{0,1}=-10$

Einsetzen der Koordinaten des betrachteten Punkts $(1,5\mid g(1,5))$ in die allgemeine Geradengleichung $n(x)=mx+b$ mit $m_s=-10$ liefert $b.$

Durch Gleichsetzen von $n(x)$ und $h(x)$ kann der Punkt auf dem Hangprofil ermittelt werden, in dem die blau eingezeichnete Strecke auf diesen trifft.

Ermitteln des Abstandes zwischen den beiden Endpunkten der blauen Strecke liefert dann den gesuchten Abstand.

Für die Stammfunktionen von $v(x)$ folgt:

$V(x)=-\ln(x)+C$

Da der Wertebereich des Logarithmus durch $\mathbb{R}$ und der Definitionsbereich durch $\mathbb{R}^+$ gegeben ist, liefert also jeder Wert $C\in\mathbb{R}$ einen Wert $k\in\mathbb{R}^+,$ sodass $C=\ln(k)$ gilt. Damit folgt mit Hilfe der Logarithmusregeln für die Form der Stammfunktionen:

$\begin{array}[t]{rll} V(x)&=&-\ln(x)+\ln(k) \\[5pt] &=&\ln\left(\dfrac{k}{x}\right) \\[5pt] &=&s_k(x) \end{array}$

Auflösen der Gleichung $s_k(0,25)=p(0,25)$ nach $k$ mit dem CAS liefert:

$k=0,25\cdot\mathrm e^{\frac{31}{32}}$

Mit dem solve-Befehls des CAS ergibt sich:

$\begin{array}[t]{rll} s_k(x)&=&p(x) \quad \scriptsize \mid k=0,25\cdot\mathrm e^{\frac{31}{32}} \\[5pt] x_1&=&0,25 \\[5pt] x_2&\approx&2,07 \end{array}$

Die zugehörigen Funktionswerte folgen mit:

$\begin{array}[t]{rll} p(0,25)&=&-\dfrac{1}{2}\cdot0,25^2+1 \\[5pt] &\approx&0,97 \end{array}$

$\begin{array}[t]{rll} p(2,07)&=&-\dfrac{1}{2}\cdot2,07^2+1 \\[5pt] &\approx&-1,15 \end{array}$

Für die Steigung der gesuchten Gerade $g$ folgt damit:

$\dfrac{-1,15-0,97}{2,07-0,25}\approx-1,16$

Einsetzen der Steigung sowie der Koordinaten eines Schnittpunktes in die allgemeine Geradengleichung liefert:

$\begin{array}[t]{rll} g(x)&=&m\cdot x+b &\quad \scriptsize \mid\; (0,25 \mid 0,97) \\[5pt] 0,97&=&-1,16\cdot0,25+b &\quad \scriptsize \mid\;+0,29 \\[5pt] 1,26&=&b \end{array}$

Eine Gleichung der Geraden, die durch die beiden Schnittpunkte verläuft, ist somit gegeben durch $g(x)=-1,16\cdot x+1,26.$

Für die Flächeninhalte der beiden Flächenteile gilt somit:

Rechenweg anzeigen

$A_1 \approx 0,5$

Rechenweg anzeigen

$A_2 \approx& 0,64$

Das Verhältnis der beiden Flächeninhalte folgt also mit:

$\dfrac{A_1}{A_2}=\dfrac{0,5}{0,64}\approx0,78$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?