Wahlpflichtaufgabe 1 - Analysis
Die Abbildung zeigt den Graphen einer in 
definierten Ableitungsfunktion 
dritten Grades.
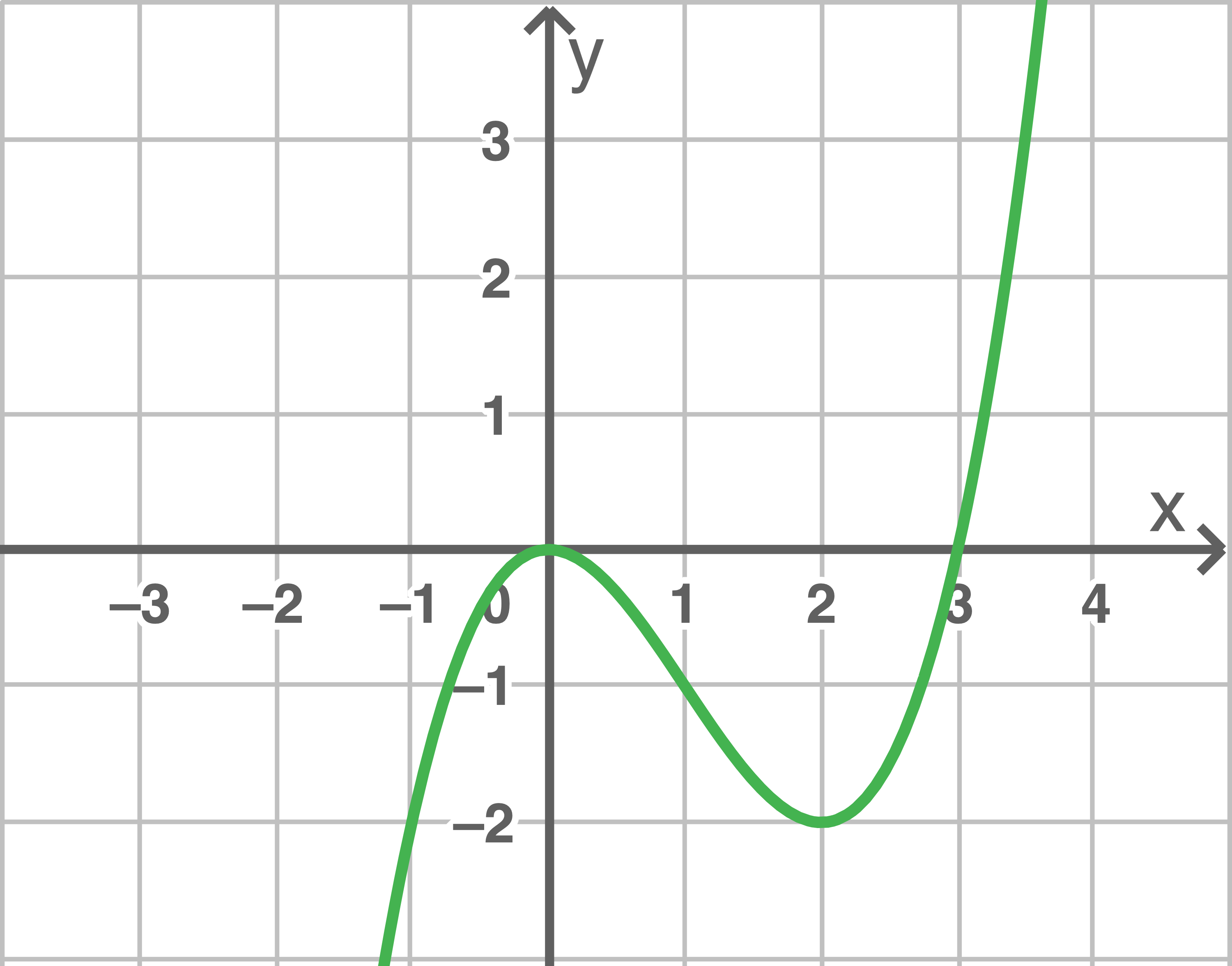
beschreibt im Intervall 
die Änderungsrate der Temperatur eines Körpers zu einem bestimmten Zeitpunkt. Dabei ist 
die seit Beobachtungsbeginn vergangene Zeit in Minuten und 
die Änderungsrate in Grad pro Minute.
a)
Bestimme eine Gleichung der Gerade, auf der die beiden Extrempunkte des Graphen von liegen.
(2 BE)
b)
Entscheide, ob der Wert des Terms 
größer als Null ist.
Begründe deine Entscheidung.
Begründe deine Entscheidung.
(3 BE)
c)
Der Graph der zugehörigen Funktion 
besitzt einen Wendepunkt mit waagerechter Tangente. Gib die -Koordinate dieses Wendepunkts an und begründe die Existenz dieses Wendepunkts mithilfe von Eigenschaften der Ableitungsfunktion bzw. ihres Graphen.
Die Ableitungsfunktion
(3 BE)
d)
Beschreibe die Entwicklung der Temperatur im angegebenen Zeitraum.
(3 BE)
e)
Zwei Minuten nach Beobachtungsbeginn beträgt die Temperatur des Körpers 
Ermittle die Temperatur zu Beobachtungsbeginn.
(4 BE)
a)
b)
Da der Graph von 
an den Stellen 
und 
Extrempunkte besitzt, gilt aufgrund des notwendigen Kriteriums für Extremstellen 
und 
Zudem lässt auch ablesen, dass
Also ist der Wert des angegebenen Terms negativ und damit nicht größer als Null.
Zudem lässt auch ablesen, dass
c)
Eine Wendestelle von ist immer eine Extremstelle von 
Es kommen zunächst also 
und 
infrage. Zudem soll der Graph von im zugehörigen Wendepunkt eine waagerechte Tangente besitzen. Es muss also 
sein.
Dies ist für erfüllt. Die gesuchte Wendestelle ist also 
Dies ist für
d)
In den ersten zwei Minuten nach Beobachtungsbeginn nimmt die Temperatur des Körpers immer schneller ab. In der darauffolgenden Minute sinkt die Geschwindigkeit, mit der die Temperatur abnimmt. Ab dem Zeitpunkt drei Minuten nach Beobachtungsbeginn nimmt die Temperatur dann zu und dies immer schneller.
e)
Der Wert, um den sich die Temperatur in den ersten beiden Minuten ändert, beschreibt den Inhalt der Fläche, die der Graph von im Intervall ![\([0;2]\)](https://mathjax.schullv.de/843d839ab55e0f672f243636b5611ab923c075cc63ed4cbee0bdb8f535440b7a?color=5a5a5a)
mit der -Achse einschließt. Der Abbildung lässt sich entnehmen, dass dieser Flächeninhalt ca. 
beträgt. Da die Fläche unterhalb der -Achse liegt, handelt es sich um eine Abnahme.
Zu Beginn muss die Temperatur also
höher gewesen sein.
Zu Beobachtungsbeginn betrug die Temperatur des Körpers 
Zu Beginn muss die Temperatur also