Wahlpflichtaufgabe 2 - Analytische Geometrie

In einem kartesischen Koordinatensystem sind gegeben ein Kreis $k_1$ mit der Gleichung $x^2+4x+y^2-2y-20=0$ sowie ein Kreis $k_2$ mit dem Radius $r_2=\sqrt{80}$ und dem Mittelpunkt $M_2(-7\mid 1)$ .

a) Ermittle die Koordinaten des Mittelpunktes $M_1$ des Kreises $k_1$ und dessen Radius $r_1$ .
Gib eine Gleichung des Kreises $k_2$ an.

Die beiden Kreise $k_1$ und $k_2$ schneiden einander in den zwei Punkten $S_1(x_1\mid y_1\gt 0)$ und $S_2(x_2\mid y_2\lt 0)$ .

Begründe zunächst ohne Rechnung, dass diese Schnittpunkte gleiche Abszissen haben und berechne dann die Koordinaten der Schnittpunkte.

b) Die Punkte $S_1$ , $S_2$ , $M_2$ und ein Punkt $T$ bilden ein Viereck mit folgenden Eigenschaften:

(1)	$\overrightarrow{M_2S_1}=\overrightarrow{S_2T}$
(2)	$\left\|\overrightarrow{M_2S_1}\right\|=\left\|\overrightarrow{M_2S_2}\right\|$
(3)	$\overrightarrow{M_2S_1}\cdot \overrightarrow{M_2S_2}\neq 0$

Schlussfolgere unter Verwendung dieser drei Eigenschaften auf die Vierecksart sowie auf die Art der Innenwinkel.

Berechne für diesen Fall die Koordinaten des Punktes $T$ .

a) $\blacktriangleright$ Mittelpunkt und Radius bestimmen

Du sollst den Mittelpunkt und den Radius des gegebenen Kreises bestimmen. Die Koordinatengleichung eines Kreises lautet

$(x-x_M)^2 + (y-y_M)^2 = r^2$

wobei $M(x_M \mid y_M)$ der Mittelpunkt und $r$ der Radius des Kreises.

Forme die gegebene Kreisgleichung mit quadratischer Ergänzung in die oben gegebene Form um, dann kannst du die Koordinaten des Mittelpunkts und den Radius ablesen.

$\begin{array}[t]{rll} x^2 + 4x + y^2 -2y -20&=&0 \\[5pt] x^2 + 4x + 4 + y^2 -2y + 1 -4 -1 -20&=&0\\[5pt] (x+2)^2 + (y-1)^2 -25&=&0\\[5pt] (x+2)^2 + (y-1)^2 &=& 25 \end{array}$

Für den Mittelpunkt gilt somit $M_1(-2 \mid 1)$ .

Für den Radius gilt:

$\begin{array}[t]{rll} r_1^2&=&25 \quad \scriptsize \mid\; \sqrt{\ }\\[5pt] r_1&=&5 \end{array}$

$\blacktriangleright$ Kreisgleichung bestimmen

Du hast den Mittelpunkt $M_2$ und den Radius $r_2$ gegeben. Setze die Werte in die oben gegebene Formel ein und bestimme so die Gleichung des Kreises.

$\begin{array}[t]{rll} (x-(-7))^2 + (y-1)^2&=&\sqrt{80}^2\\[5pt] x^2 + 14x + 49 + y^2 -2y+1&=&80\quad \scriptsize \mid\; -80\\[5pt] x^2 + 14x + 49 + y^2 -2y+1-80&=&0\\[5pt] x^2 + 14x + y^2 -2y-30&=&0 \end{array}$

$\blacktriangleright$ Schnittpunkte bestimmen

Die $y$ -Koordinaten der Mittelpunkte $M_1$ und $M_2$ stimmen überein. Somit haben die beiden Schnittpunkte die gleiche $x$ -Koordinate.

Nun sollst du das rechnerisch zeigen, das machst du, indem du die beiden Gleichungen gleichsetzt.

$\begin{array}[t]{rll} x^2 + 14x + y^2 -2y-30&=&x^2 + 4x + y^2 -2y -20 \quad \scriptsize \mid\; -y^2 \quad \mid\; +2y\\[5pt] x^2 + 14x-30&=&x^2 + 4x -20 \quad \scriptsize \mid\; +30 \quad \mid\; -x^2\\[5pt] 14x&=&4x +10 \quad \scriptsize \mid\; -4x\\[5pt] 10x&=&10 \quad \scriptsize \mid\; :10\\[5pt] x&=&1 \end{array}$

Setze nun $x=1$ in eine der Gleichungen ein um die $y$ -Koordinaten zu bestimmen.

$\begin{array}[t]{rll} 0&=&1^2 + 14 + y^2 -2y-30 \\[5pt] 0&=&y^2-2y-15 \end{array}$

Diese quadratische Gleichung kannst du mit der p-q-Formel lösen.

$\begin{array}[t]{rll} y_{1,2}&=&-\dfrac{-2}{2} \pm \sqrt{\left(\dfrac{-2}{2}\right)^2-(-15)}\\[5pt] &=&1 \pm \sqrt{16}\\[5pt] y_1&=&5\\[5pt] y_2&=&-3 \end{array}$

Die Schnittpunkte lauten also $S_1(1\mid 5)$ und $S_2(1\mid -3)$ .

b) $\blacktriangleright$ Vierecksart bestimmen

In diesem Aufgabenteil hast du die folgenden Eigenschaften des Vierecks $S_1 S_2 M_2 T$ gegeben:

$\overrightarrow{M_2 S_1} = \overrightarrow{S_2 T}$

$\mid\overrightarrow{M_2 S_1}\mid\ =\ \mid\overrightarrow{M_2 S_2}\mid$

$\overrightarrow{M_2 S_1} \cdot \overrightarrow{M_2 S_2} \ne 0$

Die Koordinaten der Punkte $S_1(1\mid 5)$ , $S_2(1 \mid -3)$ und $M_2(-7\mid 1)$ kannst du aus Aufgabenteil a) übernehmen.

Fertige eine Skizze an und interpretiere dann die drei gegebenen Eigenschaften.

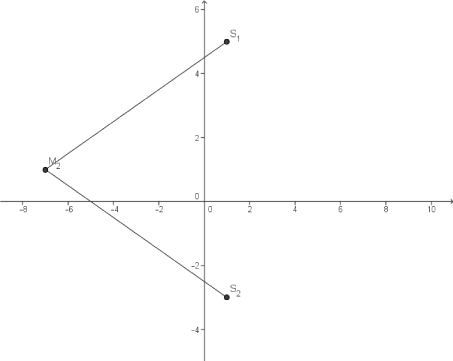Graf mit zwei Linien, die sich schneiden, und einem Punkt M im Koordinatensystem.

Aus der 1. Eigenschaft $\overrightarrow{M_2 S_1} = \overrightarrow{S_2 T}$ folgt, dass die Länge der beiden Vektoren übereinstimmt:

$\mid\overrightarrow{M_2 S_1}\mid = \mid\overrightarrow{S_2 T}\mid$

Mit der 2. Eigenschaft gilt weiter:

$\mid\overrightarrow{S_2 T}\mid = \mid\overrightarrow{M_2 S_1}\mid = \mid\overrightarrow{M_2 S_2}\mid$

Du weist nun, dass drei der vier Seiten des Vierecks gleich lang sind. Die 1. Eigenschaft bedeutet außerdem, dass die Strecken $M_2S_1$ und $S_2T$ parallel sind. Es handelt sich also um ein Parallelogramm. Bei einem Parallelogramm sind die gegenüberliegende Seiten gleich lang, somit haben alle vier Seiten des Vierecks die gleiche Länge.

Die 3. Eigenschaft gibt an, dass sich im Punkt $M_2$ kein rechter Winkel befindet. Da es sich um ein Parallelogramm handelt ist die Größe der gegenüberliegenden Winkel identisch. Zwei dieser Winkel sind also größer und zwei sind kleiner als $90^\circ$ .

Ein Parallelogramm mit gleich langen Seiten wird Raute bzw. Rhombus genannt.

$\blacktriangleright$ Koordinaten von Punkt $\boldsymbol{T}$ bestimmen

Nun sollst du noch die Koordinaten des fehlenden Punkts $T$ bestimmen.

Die 1. Eigenschaft des Vierecks ist $\overrightarrow{M_2 S_1} = \overrightarrow{S_2 T}$ . Berechne diesen Vektor:

$\begin{array}[t]{rll} \overrightarrow{S_2 T}&=&\overrightarrow{M_2 S_1} \\[5pt] &=&\overrightarrow{O S_1}-\overrightarrow{O M_2}\\[5pt] &=&\begin{pmatrix}1-(-7)\\5-1\end{pmatrix}\\[5pt] &=&\begin{pmatrix}8\\4\end{pmatrix} \end{array}$

Den Ortsvektor zu $T$ erhältst du folgendermaßen:

$\begin{array}[t]{rll} \overrightarrow{OT}&=&\overrightarrow{OS_2} + \overrightarrow{S_2T} \\[5pt] &=&\begin{pmatrix}1\\-3\end{pmatrix} + \begin{pmatrix}8\\4\end{pmatrix}\\[5pt] &=&\begin{pmatrix}9\\1\end{pmatrix} \end{array}$

Der Punkt $T$ lautet somit $T(9 \mid 1)$ .