Wahlpflichtaufgabe 1 - Analysis

Betrachtet wird die Funktion $\phi$ mit $y=\phi(x)= \frac{1}{\sqrt{ 2\pi}}\mathrm e^{-\frac{1}{2}x^2}, x\in \mathbb{R}$ .

Ihr Graph wird als Gaußsche Glockenkurve bezeichnet.

Weise nach, dass die Gaußsche Glockenkurve symmetrisch zur y-Achse ist.

Die Gaußsche Glockenkurve besitzt genau zwei Wendepunkte.
Berechne die Abszisse dieser Wendepunkte.

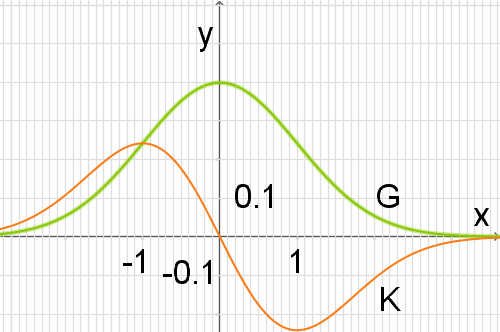
Im untenstehenden Koordinatensystem sind die Gaußsche Glockenkurve G sowie ein weiterer Funktionsgraph K dargestellt.

Begründe anhand von drei Eigenschaften der Funktion $\phi$ oder ihres Graphen, dass es sich bei der Kurve K um den Graphen der Ableitungsfunktion $\(\phi$ handeln kann.

Grafik mit zwei Kurven in grün und orange auf einem karierten Hintergrund.

Abb. 1

Die Gaußsche Glockenkurve spielt in der Stochastik eine wichtige Rolle bei der Approximation der Binominalverteilung durch die Standardnormalverteilung.
So lässt sich eine Wahrscheinlichkeit $P(D)$ näherungsweise durch das folgende bestimmte Integral berechnen.

$P(D)\approx\displaystyle\int_{-1,6}^{1,6} \phi (x) \;\mathrm dx$

Berechne dieses bestimmte Integral näherungsweise mithilfe eines Verfahrens der numerischen Integration; verwende acht Teilintervalle.

Bildnachweise [nach oben]

[1]

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$\blacktriangleright$ Zeigen, dass die Gaußsche Glockenkurve symmetrisch zur y-Achse ist

Der Graph einer Funktion $f$ ist achsensymmetrisch, wenn gilt:

$f(x)=f(-x)$

Setze also für $-x$ in den Funktiosterm $\phi(x)$ ein.

$\begin{array}[t]{rll} \phi(-x)&=&\dfrac{1}{\sqrt{2\pi}}\mathrm e^{-\frac{1}{2}(-x)^2} \\[5pt] &=&\frac{1}{\sqrt{2\pi}}\mathrm e^{-\frac{1}{2}x^2} \\[5pt] & = & \phi(x) \end{array}$

Damit hast du gezeigt, dass die Gaußsche Glockenkurve symmetrisch zur $y$ -Achse ist.

$\blacktriangleright$ Abszissen der Wendepunkte berechnen

Du hast die Funktion $\phi$ gegeben und sollst deren Graph auf Wendepunkte untersuchen. Für eine Wendestelle $x_W$ benötigst du die beiden folgenden Kriterien:

Notwendiges Kriterium: $\, \phi ‘‘(x_W)=0$
Hinreichendes Kriterium: $\, \phi ‘‘‘(x_W)\neq 0$

Bestimme die ersten drei Ableitungsfunktionen $\phi ‘$ , $\phi ‘‘$ und $\phi ‘‘‘$ .
Wende das notwendige Kriterium an, indem du $\phi ‘‘(x)=0$ setzt und nach $x$ löst.
Überprüfe das hinreichende Kriterium, indem du die Lösung aus 2. in $\phi ‘‘‘(x)$ einsetzt.

1. Schritt: Ableitungsfunktionen bestimmen

$\begin{array}[t]{rll} \phi‘(x)&=&\frac{1}{\sqrt{2\pi}}\cdot \left(-\frac{1}{2}\right)\cdot 2x \cdot e^{-\frac{1}{2}x^2} \\[5pt] &=&-\frac{x}{\sqrt{2\pi}} \cdot e^{-\frac{1}{2}x^2} \end{array}$

$\phi‘‘(x) =\left(-\frac{1}{\sqrt{2\pi}} +\frac{x^2}{\sqrt{2\pi}} \right)\cdot e^{-\frac{1}{2}x^2}$

Vollständige Lösung anzeigen

$\begin{array}[t]{rll} \phi‘‘‘(x)&=& \end{array}$

Vollständige Lösung anzeigen

2. Schritt: Notwendiges Kriterium anwenden

$\phi ‘‘(x)$

$\phi‘‘(x)=0$

$\left(-\frac{1}{\sqrt{2\pi}} +\frac{x^2}{\sqrt{2\pi}} \right)=0$

$\begin{array}[t]{rll} x_{W_{1,2}}&=&\pm 1 \end{array}$

Vollständige Lösung anzeigen

3. Schritt: Hinreichendes Kriterium überprüfen

$\phi$

$x_{W_{1,2}}=\pm 1$

$x_{W_1} = -1$

$x_{W_2} = 1$

$\blacktriangleright$ Begründen, dass es sich bei der Kurve K um den Graph der Ableitung $\boldsymbol{\phi‘(x)}$ handeln kann

Wenn du den Graphen einer Funktion $f$ gegeben hast, dann kannst du verschiedene Aussagen über den Graphen der Ableitung $f‘$ treffen.

Graph der Funktion $f$	Graph der Funktion $f‘$
Hoch- und Tiefpunkte	Nullstellen
Wendepunkte	Hoch- und Tiefpunkte

Der Graph der Funktion $\phi(x)$ hat an den Stellen $x=\pm 1$ jeweils einen Wendepunkt. Dies bedeutet, dass der Graph der Ableitung an der Stelle $x= \pm 1$ Extremstellen hat. Wenn du dir das Schaubild K anschaust, hat dieses bei $x=-1$ einen Hochpunkt und bei $x=1$ einen Tiefpunkt.

Aus dem Schaubild der Funktion $\phi$ kannst du ablesen, dass der Graph der Funktion im Punkt H $(0,4\;|\;0)$ einen Hochpunkt hat, das bedeutet, dass der Graph der Ableitung an dieser Stelle eine Nullstelle haben muss. Auch das ist im Schaubild K erfüllt.

Somit hast du gezeigt, dass das Schaubild K die Ableitung des Schaubildes G, also der Funktion $\phi(x)$ darstellen kann.

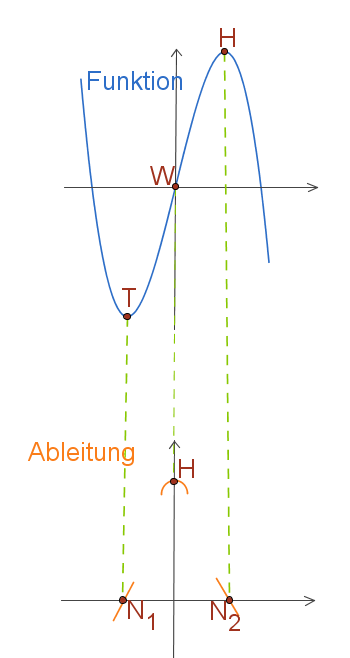Grafik einer Funktion mit Ableitungen und wichtigen Punkten im Koordinatensystem.

Abb. 1: Graphisch ableiten

$\blacktriangleright$ Integral berechnen

In dieser Aufgabe sollst du das bestimmte Integral $\displaystyle\int_{-1,6}^{1,6} \phi(x) \;\mathrm dx$ mit Hilfe eines Verfahrens der numerischen Integration berechnen. Dabei sollst du acht Intervalle verwenden. Du kannst zum Beispiel das Trapezverfahren verwenden.

Mit $d=\frac{b-a}{n}=\frac{x_n-x_0}{n}$ erhälst du

$A\approx \sum^n_{k=1}\; \frac{1}{2} \cdot \left( f(x_{k-1})+ f(x_k) \right) \cdot d$

Da du acht Intervalle verwenden sollst, sollten diese einen Abstand von 0,4 haben. Am einfachsten ist es, wenn du für jedes Intervall den Teilwert berechnest und anschließend die Ergebnisse aufsummierst. Da es sich um einen symmetrischen Graphen handelt, reicht es, wenn du den Flächeninhalt zum Beispiel von -1,6 bis zur $y$ -Achse berechnest und am Ende diesen Flächeninhalt verdoppelst.

$d=\frac{1,6-(-1,6)}{8} = 0,4$

$\begin{array}[t]{rll} A_1&\approx& \frac{1}{2} \left( f(-1,6) + f(-1,2) \right)\cdot 0,4 \\[5pt] &\approx& \frac{1}{2}(0,11 + 0,19 ) \cdot 0,4 \\[5pt] &\approx& \frac{1}{2}\cdot 0,30 \cdot 0,4 \\[5pt] &\approx& 0,06 \end{array}$

$\begin{array}[t]{rll} A_2&\approx& \frac{1}{2} \left( f(-1,2) + f(-0,8) \right) \cdot 0,4 \\[5pt] &\approx& \frac{1}{2}(0,19 + 0,29 ) \cdot 0,4\\[5pt] &\approx& \frac{1}{2}\cdot 0,48 \cdot 0,4 \\[5pt] &\approx& 0,096 \end{array}$

$\begin{array}[t]{rll} A_3&\approx& 0,124 \\[5pt] \end{array}$

$\begin{array}[t]{rll} A_4&\approx& 0,178 \\[5pt] \end{array}$

$A\approx 0,916$

Vollständige Lösung anzeigen

Für das bestimmte Integral ergibt sich mit dem Trapezverfahren unter Verwendung von acht Teilintervallen ein Wert von ungefähr $0,916$ .

Bildnachweise [nach oben]

[1]

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?