Pflichtaufgabe 1 - Analysis

Gegeben sind die Funktionen $f_k$ in ihrem größtmöglichen Definitionsbereich durch

$y=f_k(x)=\dfrac{10x-k}{x^2}$ $\quad$ mit $k\in\mathbb{R}, k>0$ . $\quad$ Ihre Graphen seien $G_k$ .

Geben Sie den größtmöglichen Definitionsbereich der Funktionen $f_k$ an und ermitteln Sie die Nullstellen der Funktionen $f_k$ .

Untersuchen Sie das Verhalten der Funktionen $f_k$ für $x\rightarrow \pm\infty$ und geben Sie Gleichungen aller Asymptoten der Graphen $G_k$ an.

Berechnen Sie die Koordinaten der lokalen Extrempunkte der Graphen $G_k$ und bestimmen Sie deren Art.

Ermitteln Sie eine Gleichung der Ortskurve der lokalen Extrempunkte der Graphen $G_k$ .

Die Graphen $G_k$ besitzen jeweils genau einen Wendepunkt $W_k\left(\frac{3k}{10}\mid \frac{200}{9k}\right)$ .

Stellen Sie eine Gleichung der Tangenten $t_k$ an die Graphen $G_k$ in ihren Wendepunkten $W_k$ auf.

[mögliche Gleichung für $t_k$ zur Kontrolle: $y=t_k(x)=-\dfrac{1.000}{27k^2}x+\dfrac{100}{3k}$ ]

Jede dieser Tangenten $t_k$ bildet mit den Koordinatenachsen ein Dreieck.
Zeigen Sie, dass der Flächeninhalt dieser Dreiecke unabhängig vom Parameter $k$ ist.

In dem gegebenen Koordinatensystem (siehe Arbeitsblatt auf der folgenden Seite) sind Ausschnitte des Graphen $G_2$ sowie eines weiteren Graphen $G_k\cdot(k^*\in N)$ als Kurven $K_1$ und $K_2$ dargestellt.
Untersuchen Sie, welche der Kurven zum Graphen $G_2$ gehört und ermitteln Sie den Wert des Parameters $k^*$ .

Zeichnen Sie in das gegebene Koordinatensystem die Ortskurve der lokalen Extrempunkte im Intervall $0,4\leq x\leq 3$ .

Die Maßzahl des Inhalts einer Fläche $F$ werde wie folgt berechnet:

$A_1=\mathop{\displaystyle\int}\limits_{0,2}^{0,4}f_2(x)\mathrm dx+\mathop{\displaystyle\int}\limits_{0,4}^{1}\dfrac{5}{x}\mathrm dx-\mathop{\displaystyle\int}\limits_{0,5}^{1}f_k* (x)dx$

Beschreiben Sie die Fläche $F$ und kennzeichnen Sie diese im Arbeitsblatt.

Es sei $A_2=\mathop{\displaystyle\int}\limits_{0,2}^{0,4}f_2(x)\mathrm dx+\mathop{\displaystyle\int}\limits_{0,4}^{0,5}\dfrac{5}{x} \mathrm dx+\mathop{\displaystyle\int}\limits_{0,5}^{1}(\dfrac{5}{x}-f_k*(x))\mathrm dx$ .

Weisen Sie nach, dass gilt: $A_1=A_2$ .

Arbeitsblatt zu Aufgabe 1

Diagramm mit zwei Kurven in einem Gitter, das mathematische oder statistische Daten darstellt.

a) $\blacktriangleright$ Größtmöglichen Definitionsbereich bestimmen

In der ersten Aufgabe ist eine Funktionenschar gegeben, die durch die Gleichung

$\boldsymbol{f_k(x)=\dfrac{10x-k}{x^2}}$

dargestellt wird. Der Parameter $k$ gehört zur Menge der rationalen Zahlen und ist echt größer als Null. Du sollst den Definitionsbereich und die Nullstellen angeben, verschiedene Grenzwerte berechnen, die Gleichungen aller Asymptoten aufstellen, sowie die Extrempunkte und deren Ortskurve bestimmen.

Der Definitionsbereich $\mathbb{D}$ gibt alle Werte an, für die die Funktion definiert ist, die man also in den Funktionsterm einsetzen darf.

Nicht definiert sind Funktionen dann, wenn...

...der Nenner der Funktion den Wert $0$ annimmt.
...der Radikand unter einer Wurzel einen negativen Wert hat.
...das Argument einer $\log$ - oder $\ln$ -Funktion einen negativen Wert annimmt.

Ergibt der Nenner beim Einsetzen eines $x$ -Wertes Null, hat er an dieser Stelle eine Definitionslücke, da man in keinem Fall durch Null teilen darf!

Der Nenner der gegebenen Funktion ist Null, wenn $x=0$ gilt. Der Wert $x=0$ darf also nicht in den Funktionsterm eingesetzt werden.

Daraus ergibt sich der Definitionsbereich $\mathbb{D}=\mathbb{R}\setminus \{0\}$ .

Du kannst den Definitionsbereich auch folgendermaßen schreiben: $\mathbb{D}=\left\{x\mid x\in\mathbb{R}\land x\neq0\right\}$

$\blacktriangleright$ Nullstellen berechnen

Nullstellen sind die $x$ -Werte, an denen $\boldsymbol{f(x)=0}$ gilt. Um diese zu bestimmen, musst du den Funktionsterm mit Null gleichsetzen.

Bei der gegebenen Funktion handelt es sich um eine gebrochen rationale Funktion. Diese hat den Funktionswert Null, wenn der Zähler Null ist:

$\begin{array}{rlll} f_k(x)&=&0&\scriptsize\\[5pt] \dfrac{10x-k}{x^2}&=&0&\scriptsize \mid\;\cdot x^2\\[5pt] 10x-k&=&0&\scriptsize \mid\;+k\\ 10x&=&k&\scriptsize \mid\;:10\\ x&=&\dfrac{k}{10}&\scriptsize\\[5pt] \end{array}$

An den Stellen $x=\frac{k}{10}$ befinden sich die Nullstellen der Funktionen $f_k$ .

$\blacktriangleright$ Grenzwerte für $\boldsymbol{x\rightarrow\pm\infty}$ berechnen

Um die Grenzwerte der Funktion $f_k$ zu bestimmen, muss die Funktion erst umformuliert werden:

$\begin{array}{r@{\;=\;}l@{\hspace{1cm}}l} \dfrac{10x-k}{x^2}&\dfrac{10x}{x^2}-\dfrac{k}{x^2}=\dfrac{10}{x}-\dfrac{k}{x^2}&\scriptsize \\ \end{array}$

Mit dieser umgeformten Funktionsgleichung kannst du nun den Grenzwert bestimmen:

Um zu bestimmen, welchen Wert die Funktion annimmt, wenn der eingesetzte $x$ - Wert gegen $+ \infty$ oder $- \infty$ strebt, setzt du gedanklich sehr große bzw. sehr kleine Beispielwerte ein.

$\begin{array}{rlll} \displaystyle\lim_{x\rightarrow\pm\infty}f_k(x)&=&\displaystyle\lim_{x\rightarrow\pm\infty}\underbrace{\dfrac{10}{x}}_{\to0}-\underbrace{\dfrac{k}{x^2}}_{\to0}&\scriptsize\\ &=&0&\scriptsize\\ \end{array}$

Nimmt $x$ unendlich große Werte an, wird der Nenner sehr groß, der Bruch dagegen sehr klein. Der Grenzwert beträgt folglich 0.

$\blacktriangleright$ Gleichung aller Asymptoten bestimmen

Gerade hast du gezeigt, dass die Funktion im Unendlichen gegen den Wert $y=0$ strebt.

Diese Gleichung entspricht der waagrechten Asymptote.

Die senkrechte Asymptote befindet sich an der Stelle, an der die Funktion nicht definiert ist. Die Gleichung lautet also $x=0$ .

$\blacktriangleright$ Art und Lage der Extrempunkte berechnen

Um die Extrempunkte des Graphen von $f_k$ zu bestimmen, musst du die Funktion $f_k$ auf Minima bzw. Maxima untersuchen. Für diese sind die folgenden Kriterien zu erfüllen:

Notwendige Bedingung: $\boldsymbol{f_k‘(x)=0}$
Hinreichede Bedingung: $\boldsymbol{f_k‘‘(x) > 0}$ für ein Minimum und $\boldsymbol{f_k‘‘(x) < 0}$ für ein Maximum.

Hast du schließlich alle $x$ -Werte bestimmt, für die ein Minimum bzw. Maximum vorliegt, so kannst du besagten $x$ -Wert in den Term der Funktion $f_k$ einsetzen und erhältst so die entsprechende $y$ -Koordinate.

1. Schritt: Leite die Funktion nach $\boldsymbol{x}$ ab

Da die Funktion $f$ eine gebrochen rationale Funktion ist, musst du die Quotientenregel verwenden, um $f$ abzuleiten.

$\begin{array}{rllll} f_k‘(x)&=&\left[\dfrac{10x-k}{x^2}\right]‘&\scriptsize \\[5pt] &=&\dfrac{x^2\cdot10-(10x-k)\cdot2x}{x^4}&\scriptsize \\[5pt] &=&\dfrac{10x^2-20x^2+2kx}{x^4}&\scriptsize \\[5pt] &=&\dfrac{x\cdot(10x-20x+2k)}{x\cdot(x^3)}&\scriptsize \\[5pt] &=&\dfrac{-10x+2k}{x^3}&\scriptsize \\[5pt] &=&\dfrac{2k-10x}{x^3}&\scriptsize \\[5pt] \end{array}$

2. Schritt: Setze den Term der Ableitung mit Null gleich

Im Folgenden wollen wir überprüfen, für welche $x$ die notwendig Bedingung $\boldsymbol{f_k‘(x)=0}$ erfüllt ist.

$\begin{array}{rllll} f_k‘(x)&=&0&\scriptsize \\[5pt] \dfrac{2k-10x}{x^3}&=&0&\scriptsize \mid\;\cdot x^3\\ 2k-10x&=&0&\scriptsize \mid\;+10x\\ 10x&=&2k&\scriptsize \mid\;: 10\\[5pt] x&=&\dfrac{1}{5}k&\scriptsize\\ \end{array}$

Mögliche Minima bzw. Maxima befinden sich an der Stelle $x=\frac{k}{5}$ .

3. Schritt: Zweite Ableitung auf Sattelpunkt überprüfen Mit dem hinreichenden Kriterium $\boldsymbol{f_k‘‘(x)\neq0}$ überprüfst du, ob es sich wirklich um einen Extrempunkt handelt.

Gilt nämlich $f_k‘‘(x)=0$ , so handelt es sich nicht um einen Hoch- oder Tiefpunkt, sondern um einen Sattelpunkt.

Die zweite Ableitung berechnest du folgendermaßen:

$\begin{array}{rllll} f_k‘‘(x)&=&\left[\dfrac{2k-10x}{x^3}\right]‘&\scriptsize \\[5pt] &=&\dfrac{-10x^3-(2k-10x)\cdot3x^2}{x^6}&\scriptsize \\[5pt] &=&\dfrac{-10x^3-6kx^2+30x^3}{x^6}&\scriptsize \\[5pt] &=&\dfrac{-10x-6k+30x}{x^4}&\scriptsize \\[5pt] &=&\dfrac{20x-6k}{x^4}&\scriptsize\\[5pt] \end{array}$

Überprüfe nun die hinreichende Bedingung. Für $x=\frac{k}{5}$ gilt:

$\begin{array}{rlll} f_k‘‘\left(\dfrac{k}{5}\right)&=&\dfrac{20\cdot \dfrac{k}{5}-6k}{\left(\dfrac{k}{5}\right)^4}&\scriptsize \\ &=&(4k-6k)\cdot\dfrac{5^4}{k^4}&\scriptsize\\ &=&\dfrac{-2k\cdot5^4}{k^4}&\scriptsize \\[5pt] &=&\dfrac{-1.250}{k^3}&\scriptsize \\ &\neq&0&\scriptsize\\ \end{array}$

Nun hast du gezeigt, dass es sich an der Stelle $\boldsymbol{x=\frac{k}{5}}$ um die Extrempunkte der Graphen und nicht um Sattelpunkte handelt.

4. Schritt: Bestimme die $y$ -Koordinate des Extrempunkts

Die $y$ -Koordinate bestimmst du durch Einsetzen des $x$ -Wertes in den ursprünglichen Funktionsterm.

$\begin{array}{rllll} f_k&=&\left(\dfrac{k}{5}\right)&\dfrac{10\cdot\dfrac{k}{5}-k}{\left(\frac{k}{5}\right)^2}&\scriptsize\\[5pt] &=&\dfrac{25}{k}&\scriptsize\\ \end{array}$

Die Extrempunkte der Funktionenschar besitzen die Koordinaten $\boldsymbol{E_k\left(\frac{k}{5}|\frac{25}{k}\right)}$ .

Ob es sich um einen Hoch- oder Tiefpunkt handelt, findest du heraus, indem du den Funktionswert der zweiten Ableitung an der $x$ -Koordinate des Extrempunktes betrachtest.

$f‘‘(x) < 0\Rightarrow \text{Hochpunkt}$ $f‘‘(x) > 0\Rightarrow \text{Tiefpunkt}$

Die zweite Ableitung und ihren Wert an der Stelle $x=\frac{k}{5}$ hast du bereits zuvor berechnet:

$f_k‘‘(x)=\frac{20x-6k}{x^4}$

$f_k‘‘\left(\frac{k}{5}\right)=\frac{-1250}{k^3}$

Laut Aufgabenstellung ist der Parameter $k$ stets positiv. Da der Nenner $k^3$ daher immer positiv ist, gilt $\dfrac{-1250}{k^3} < 0$ . Es handelt sich bei den Extrempunkten folglich um Hochpunkte.

$\blacktriangleright$ Ortskurve der Extrempunkte ermitteln

Die Koordinaten der Extrempunkte in Abhängigkeit von $k$ hast du bereits ermittelt: $\text{E}_k\left(\frac{k}{5}\mid \frac{25}{k}\right)$ . Für die $x$ -Koordinate gilt also: $x_{\text{E}}=\frac{k}{5}$ .

Formst du diese Gleichung nach $k$ um, ergibt sich $\boldsymbol{k=5x}$ .

Diesen Wert von $k$ musst du in die $y$ -Koordinate der Hochpunkte einsetzen, um die Ortskurve zu bestimmen, auf der alle Hochpunkte der Funktionenschar liegen.

$\begin{array}{rllll} y_{\text{E}}&=&\dfrac{25}{k}&\scriptsize \\[5pt] &=&\dfrac{25}{5x}&\scriptsize \\[5pt] &=&\dfrac{5}{x}&\scriptsize\\ \end{array}$

Auf dem Graphen der Funktion $y_{\text{E}}$ , der durch die Gleichung $y_{\text{E}}=\dfrac{5}{x}$ dargestellt werden kann, liegen alle Hochpunkte der Funktionenschar $f_k$ .

b) $\blacktriangleright$ Gleichung der Wendetangente t $_4$ aufstellen

Willst du die Tangente an einen Graphen an einer beliebigen Stelle $x_0$ bestimmen, verwendest du am Besten folgende Gleichung:

$y=t(x)=f‘(x_0)(x-x_0)+f(x_0)$

Hier stellt $f$ die Funktion dar, an die die Tangente angelegt werden soll. $x_0$ gibt die Stelle an und $x$ die Veränderliche.

Um die Tangente t $_k$ im Wendepunkt W $_k$ zu bestimmen, musst du die die notwendigen Angaben ermitteln. Da die Tangente an den Wendepunkt $W(\frac{3k}{10} \mid \frac{200}{9k})$ angelegt werden soll, muss hier $x_0=\frac{3k}{10}$ gelten.

1. Schritt: Funktionswert $\boldsymbol{f‘(x_0)}$ berechnen

Die erste Ableitung der Funktion $f_k$ in Abhängigkeit von $k$ hast du bereits berechnet:

$\begin{array}{rllll} f‘_k(x)&\dfrac{2k-10x}{x^3}&\scriptsize\\ \end{array}$

Durch Einsetzen von $x_0$ erhältst du den Funktionswert $f‘(x_0)$ .

2. Schritt: Tangentengleichung aufstellen

Mit den bekannten Werten ergibt sich die Funktionsgleichung der Tangente:

$\begin{array}{rllll} t_k(x)&=&f_k‘(x_0)(x-x_0)+f_k(x_0)&\scriptsize \\[5pt] &=&\dfrac{2k-10x_0}{x_0^3}(x-x_0)+\dfrac{10x_0-k}{x_0^2}&\scriptsize \\[5pt] &=&\dfrac{2kx-10x_0x}{x_0^3}-\dfrac{2kx_0-10x_0^2}{x_0^3} +\dfrac{10x_0-k}{x_0^2}&\scriptsize \\[5pt] &=&\dfrac{2kx-10x_0x}{x_0^3}-\dfrac{2k-10x_0}{x_0^2} +\dfrac{10x_0-k}{x_0^2}&\scriptsize \\[5pt] &=&\dfrac{2kx-10x_0x}{x_0^3}+\dfrac{-3k+20x_0}{x_0^2} &\scriptsize \\[5pt] \end{array}$

Nun soll die Tangente am allgemein angegebenen Wendepunkt $W\left( \frac{3k}{10}\mid \frac{200}{9k}\right)$ angelegt werden. Das heißt, es gilt: $\boldsymbol{x_0=\frac{3k}{10}}$ und wir können einsetzen:

$\begin{array}{rllll} t_k(x)&=&f_k‘(x_0)(x-x_0)+f_k(x_0)&\scriptsize \\[5pt] &=&\dfrac{2kx-10x_0x}{x_0^3}+\dfrac{-3k+20x_0}{x_0^2} &\scriptsize \\[5pt] &=&\dfrac{2kx-10\frac{3k}{10}x}{\frac{3k}{10}^3}+\dfrac{-3k+20\frac{3k}{10}}{\frac{3k}{10}^2} &\scriptsize \\[5pt] &=&1.000 \cdot \dfrac{2kx-3kx}{27k^3}+100\cdot \dfrac{-3k+2\cdot 3k}{9k^2} &\scriptsize \\[5pt] &=&1.000 \cdot \dfrac{-kx}{27k^3}+100\cdot \dfrac{3k}{9k^2} &\scriptsize \\[5pt] &=&-\dfrac{1.000}{27k^2}\cdot x+\dfrac{100}{3k} &\scriptsize \\[5pt] \end{array}$

Die Tangente $t_k(x)=-\dfrac{1.000}{27k^2}\cdot x+\dfrac{100}{3k}$ verläuft durch den Wendepunkt W $_k$ .

$\blacktriangleright$ Unabhängigkeit des Flächeninhalts vom Parameter $\boldsymbol{k}$ zeigen

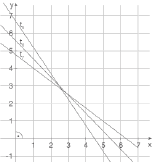Diagramm mit mehreren Linien auf einem Koordinatensystem.

Wie du an dieser Skizze erkennen kannst, handelt es sich bei allen Dreiecken, die die Tangenten mit den Koordinatenachsen einschließen, um rechtwinklige Dreiecke.

Den Flächeninhalt eines solchen Dreiecks berechnet man nach folgender Formel:

$A_{\Delta}=\frac{1}{2}\cdot g \cdot h$

Hast du die Länge der beiden Seiten berechnet, kannst du den gesamten Flächeninhalt nach dieser Formel bestimmen. Erhältst du letztlich eine Maßzahl, die unabhängig vom Parameter $k$ ist, so hast du die Behauptung aus der Aufgabe bewiesen.

1. Schritt: Länge der Grundseite $\boldsymbol{g}$ ermitteln

Um die Länge der Grundseite zu ermitteln, musst du den Schnittpunkt der Tangente mit der $x$ -Achse ermitteln. Der Abstand zwischen dem Ursprung und diesem Schnittpunkt entspricht der gesuchten Länge.

Der Schnittpunkt mit der $x$ -Achse entspricht der Nullstelle. Diese kannst du ermitteln, indem du $\boldsymbol{t_k(x)=0}$ setzt und nach $x$ auflöst:

$\begin{array}{rllll} 0&=&t_k(x)&\scriptsize \\[5pt] 0&=&-\dfrac{1.000}{27k^2}\cdot x+\dfrac{100}{3k} &\scriptsize \mid\; +\frac{1.000}{27k^2}\cdot x\\[5pt] \dfrac{1.000}{27k^2}\cdot x&=&\dfrac{100}{3k} &\scriptsize \mid\; \cdot \frac{27k^2}{1.000}\\[5pt] x&=&\dfrac{100}{3k}\cdot \dfrac{27k^2}{1.000} = \dfrac{27k^2}{10 \cdot 3k} = \dfrac{9k}{10}& \end{array}$

Die Tangente $t_k$ schneidet die $x$ -Achse an der Stelle $x=\frac{9k}{10}$ . Die Grundseite $g$ hat damit eine Länge von $\frac{9k}{10}$ LE.

2. Schritt: Länge der Höhe $h$ berechnen

Die Höhe des Dreiecks berechnest du auf die gleiche Weise. Allerdings interessiert hier der Abstand des Schnittpunkts der Tangente mit der $y$ -Achse vom Ursprung. Den $y$ -Achsenabschnitt erhältst du, indem du $x=0$ in den Term der Tangente einsetzt und berechnest:

$\begin{array}{rllll} t_k(x=0)&=&-\dfrac{1.000}{27k^2}\cdot 0+\dfrac{100}{3k}&\scriptsize \\[5pt] &=&\dfrac{100}{3k}&\scriptsize \end{array}$

Damit beträgt der Abstand des Schnittpunkts der Tangente mit der $y$ -Achse vom Ursprung $\frac{100}{3k}$ LE.

3. Schritt: Flächeninhalt der Dreiecke berechnen Nach der oben genannten Form und den gerade bestimmten Längen von Höhe und Grundlinie kannst du den Flächeninhalt des Dreiecks berechnen:

$\begin{array}{rllll} A_{\Delta}&=&\dfrac{1}{2}\cdot g \cdot h&\scriptsize \\[5pt] &=&\dfrac{1}{2} \cdot\dfrac{9k}{10} \cdot \dfrac{100}{3k} =\dfrac{30}{2} =15&\scriptsize \end{array}$

Der Flächeninhalt beträgt somit 15 FE und ist damit nicht vom Parameter $k$ abhängig. Die Aussage aus dem Aufgabentext wurde bewiesen.

c) $\blacktriangleright$ Teilaufgaben zu Graphen und Flächen

Im Anhang des Aufgabenblattes findest du eine Skizze von zwei Graphen, die mit $K_1$ und $K_2$ bezeichnet werden.

Deine Aufgabe ist es nun, herauszufinden, welcher der beiden Kurven zur Funktion $f_2$ mit $k=2$ gehört. Die andere Kurve bildet die Funktion $f_{k*}$ ab, deren Parameter $k*$ du bestimmen sollst.

Ein Weg, um herauszufinden, welcher der beiden Kurven die Funktion $f_2$ darstellt, sind die Nullstellen. Berechne die Nullstelle der Funktion $f_2$ und vergleiche sie mit der Skizze.
Um $k*$ zu bestimmen, gehst du umgekehrt vor: Die Nullstelle des Graphen liegt bei $x_1=0,5$ . Die allgemeine Nullstelle lautet $x_k=\dfrac{k}{10}$ . Stellst du diese Gleichung nach der gesuchten Variable um, erhältst du die gesuchte Variable.

$\blacktriangleright$ Kurve zu $\boldsymbol{f_2}$ ermitteln:

Bestimme dazu die Nullstellen der Funktion $f_2$ . Setze dazu $k=2$ in den Term der Funktionenschar $f_k$ ein und setzte anschließend den daraus resultierenden Term mit Null gleich.

$\begin{array}{rllll} f_{k=2}(x)&=&\dfrac{10x-2}{x^2}&\scriptsize \mid\; \\[5pt] 0&=&\dfrac{10x-2}{x^2}&\scriptsize \mid\; \cdot x^2 \\[5pt] 0&=&10x-2&\scriptsize \mid\; +2 \\[5pt] 2&=&10x&\scriptsize \mid\; :10 \\[5pt] x&=&\frac{1}{5}&\scriptsize \end{array}$

Die Nullstelle der Funktion $f_2$ befindet sich an $\boldsymbol{x=\frac{1}{5}}$ .

Alternativ kannst du auch verwenden, dass wir im Aufgabenteil a) gezeigt haben, dass sich Nullstellen abhängig von $k$ an $x=\frac{k}{10}$ befinden. Setzt du $k=2$ ein, erhältst du dasselbe Resultat.

Im Schaubild kannst du erkennen, dass die Kurve $K_1$ eine Nullstelle an $x=\frac{1}{5}=0,2$ aufweist. Damit gehört die Kurve $K_1$ zur Funktion $f_2$ .

$\blacktriangleright$ Parameter zur Kurve $K_2$ ermitteln:

Zuvor hast du erkannt, dass die Kurve $K_1$ zur Funktion $f_2$ gehört. Die Aufgabenstellung verlangt weiterhin, den Parameter $k*$ für die andere Kurve zu bestimmen. Die Nullstelle des Graphen liegt bei $x_1=0,5$ . Die allgemeine Nullstelle lautet $x_k=\dfrac{k}{10}$ . Setze diese Werte gleich, um den passenden Parameter für $k*$ zu erhalten:

$\begin{array}{rllll} 0,5&=&\dfrac{k*}{10}&\scriptsize \mid\; \cdot 10\\[5pt] 5&=&k*\\ \end{array}$

Für den Parameter der zweiten Kurve $K_2$ gilt demnach $\boldsymbol{k*=5}$ .

$\blacktriangleright$ Ortskurve der lokalen Extrempunkte zeichnen

In Aufgabenteil a) hast du die die Gleichung $\boldsymbol{y_{\text{E}}=\frac{5}{x}}$ aufgestellt, die die Lage der lokalen Extrempunkte der Funktion $f_k$ angibt. Du sollst diese nun in das beigefügte Koordinatensystem einzeichnen. Dazu kannst du dir eine Wertetabelle anlegen.

$\begin{array}{|c||c|c|c|c|c|c|c|c|c|} \hline \;\;\;\; x \;\;\;\; & 0,4 & 0,8 & 1,2 & 1,6 & 2,0 & 2,4 & 2,8 & 3,0\\ \hline y_{\textbf{E}} & 12,5 & 6,3 & 4,2 & 3,1 & 2,5 & 2,1 & 1,8 & 1,7\\ \hline \end{array}$

Das Schaubild sollte dann etwa wie folgt aussehen:

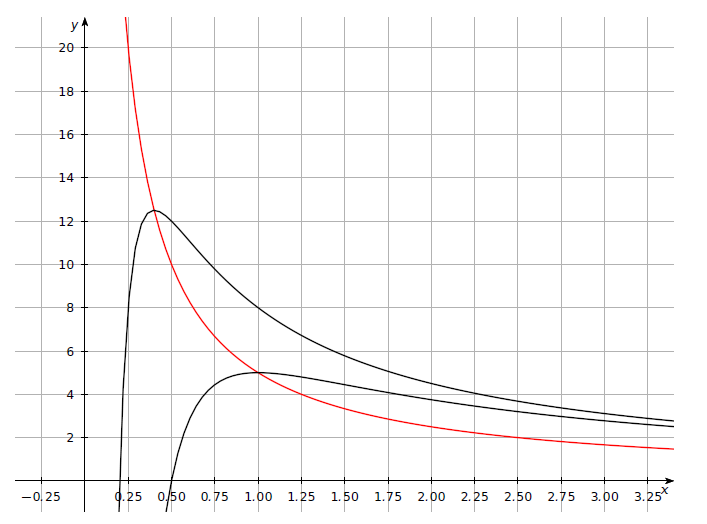
Grafik mit zwei Kurven in schwarz und rot, dargestellt in einem Koordinatensystem mit Gitterlinien.

$\blacktriangleright$ Weise nach, dass gilt: $A_1=A_2$

Um zu beweisen, dass gilt $A_1=A_2$ musst du die Gleichung für $A_2$ nach folgenden Regeln umstellen:

$\displaystyle\int_{a}^{b}f(x)+g(x)\mathrm dx=\displaystyle\int_{a}^{b}f(x)\mathrm dx+\displaystyle\int_{a}^{b}g(x)\mathrm dx$

$\displaystyle\int_{a}^{c}f(x)\mathrm dx=\displaystyle\int_{a}^{b}f(x)\mathrm dx+\displaystyle\int_{b}^{c}f(x)\mathrm dx$

Hier kannst du das zuvor gezeichnete Schaubild verwenden und die Fläche $F$ , die durch das gegebene Integral $$ \boldsymbol{F=A_1=\displaystyle\int_{0,2}^{0,4} f_2(x)\mathrm{d}x + \displaystyle\int_{0,4}^{1} \frac{5}{x} \mathrm{d}x- \displaystyle\int_{0,5}^{1} \left(f_{k*}(x)\right)\mathrm{d}x} $$ dargestellt wird, einzeichnen.

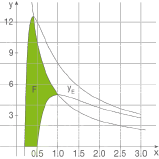Grafik einer Funktion mit einer hervorgehobenen Fläche und Achsenbeschriftungen.

Wir formen mit Hilfe der Regeln das Integral $A_2$ folgendermaßen um:

$\begin{array}{rllll} A_2&=&\displaystyle\int_{0,2}^{0,4} f_2(x)\mathrm{d}x + \displaystyle\int_{0,4}^{0,5} \frac{5}{x} \mathrm{d}x+ \displaystyle\int_{0,5}^{1} \left(\frac{5}{x}-f_{k*}(x)\right)\mathrm{d}x&\scriptsize \\[5pt] &=&\displaystyle\int_{0,2}^{0,4} f_2(x)\mathrm{d}x + \displaystyle\int_{0,4}^{0,5} \frac{5}{x} \mathrm{d}x+ \displaystyle\int_{0,5}^{1} \left(\frac{5}{x}\right)\mathrm{d}x - \displaystyle\int_{0,5}^{1} \left(f_{k*}(x)\right)\mathrm{d}x&\scriptsize \\[5pt] &=&\displaystyle\int_{0,2}^{0,4} f_2(x)\mathrm{d}x + \displaystyle\int_{0,4}^{1} \frac{5}{x} \mathrm{d}x- \displaystyle\int_{0,5}^{1} \left(f_{k*}(x)\right)\mathrm{d}x&\scriptsize \\[5pt] &=&A_1\\ \end{array}$

Damit hast du gezeigt, dass $A_1=A_2$ gilt.