Wahlpflichtaufgabe 5.2
5.2
Durch die Gleichung 
ist ein Kreis 
gegeben.
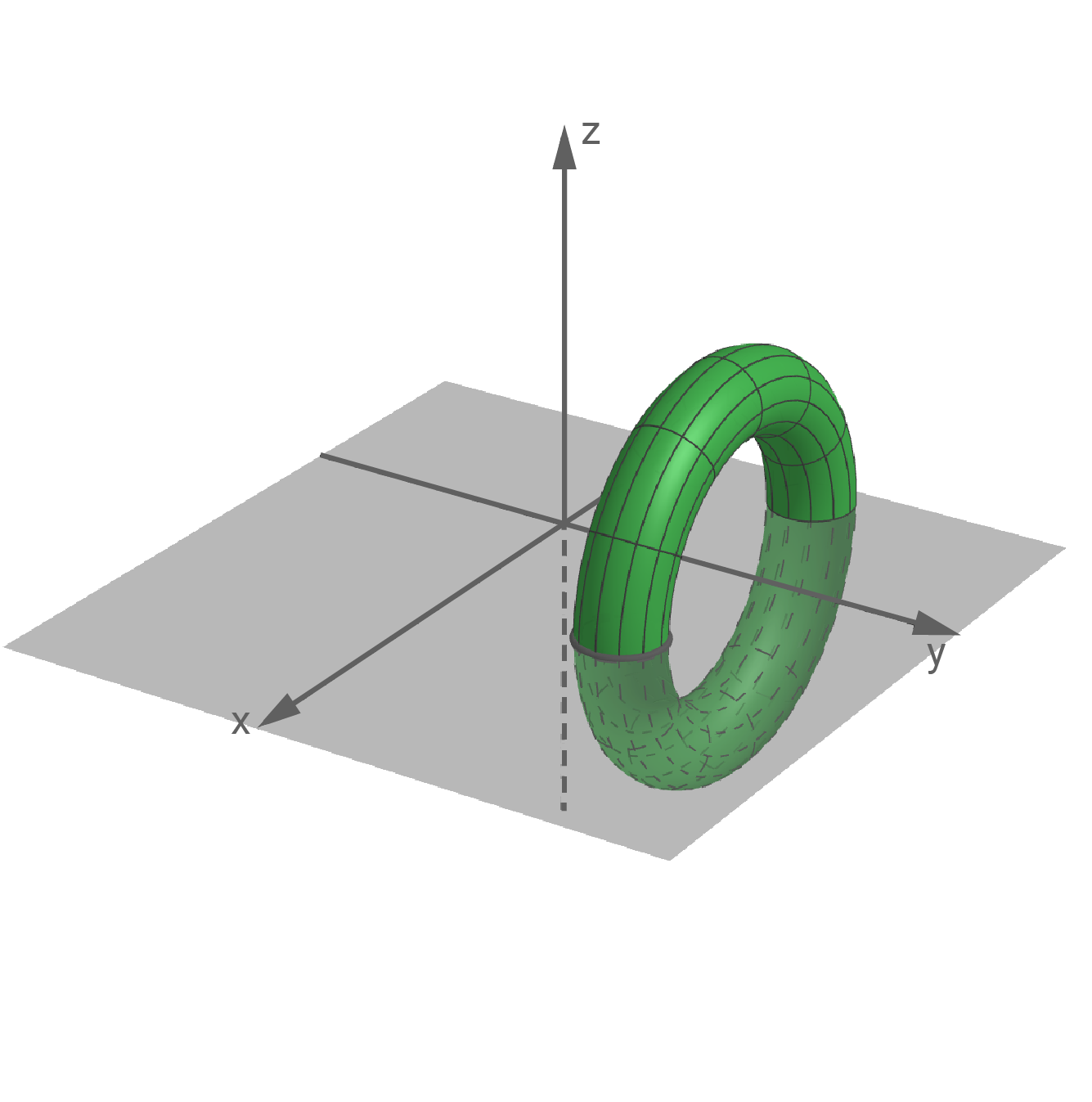
rotiert um die 
-Achse. Der dabei entstehende Körper ist in der Abbildung dargestellt.
a)
Zeige, dass der Kreis vollständig im I. Quadranten des ebenen Koordinatensystems liegt.
Der Kreis
(2 BE)
b)
Das Volumen dieses Körpers kann mit dem Term 
berechnet werden.
Erläutere die Überlegungen, die der Entwicklung des Terms zugrunde liegen.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
5.2
a)
Aus der Kreisgleichung werden die Koordinaten des Mittelpunktes des Kreises abgelesen: 
Es gilt 
Verschiebt man 
um 
in positiver und negativer 
- und -Richtung, sind die - und - Koordinaten der Punkte positiv. Deshalb befindet sich vollständig im I. Quadranten des ebenen Koordinatensystems.
b)
1. Schritt: Flächeninhalt des Kreises bestimmen
Der Flächeninhalt des Kreises wird mit 
berechnet.
2. Schritt: Umfang des erzeugten Ringes bestimmen
Durch die Rotation um die -Achse erzeugt der Kreis einen Ring.
Der Mittelpunkt des Kreises erzeugt durch die Rotation einen neuen Kreis 
dessen Umfang zur Volumenbestimmung des Ringes berechnet wird. Der Radius 
von 
entspricht dem Abstand von zur -Achse.
Der Abstand von zur -Achse entspricht 
es gilt also 
Der Umfang des erzeugten Kreises folgt mit 
3. Schritt: Volumen des Ringes bestimmen
Für das Volumen des Ringes gilt:
![\(\begin{array}[t]{rll}
V&=& A_k \cdot U_K \\[5pt]
&=& \pi \cdot r^2 \cdot 2\cdot \pi\cdot R \\[5pt]
&=& \pi \cdot 1^2 \cdot 2\cdot \pi\cdot 4
\end{array}\)](https://mathjax.schullv.de/f821da56d473cf7ea5e52e5b44b9a19d10b7ad1641f8cb6e601f697ad0619a24?color=5a5a5a)