Pflichtaufgabe 1 - Analysis

a)  Gib für die Funktionen den größtmöglichen Definitionsbereich und den Wertebereich an und ermittle die Nullstellen.
Gib für die Graphen die Koordinaten der Schnittpunkte mit der -Achse sowie eine Gleichung ihrer Asymptoten an. Beschreibe, wie die Graphen aus dem Graphen der Funktion mit
   und    ,   , hervorgehen.
Schließe daraus, ob die Funktionen lokale Extremstellen besitzen.
Zeichne den Graphen unter Einbeziehung der bisherigen Untersuchungsergebnisse.

b)  Die Strecke mit und , der Graph und die Abszissenachse schließen eine Fläche vollständig ein.
Zeige, dass die Funktion mit der Gleichung eine Stammfunktion der Funktion ist und berechne die Maßzahl des Inhalts dieser Fläche. Auf dem Graphen gibt es genau einen Punkt mit minimaler Entfernung zum Koordinatenursprung .
Stelle eine Gleichung für eine Zielfunktion in Abhängigkeit von zum Lösen dieser Extremwertproblematik auf.

c)  Berechne diejenige Stelle, an der der Graph und der Graph der Funktion mit den gleichen Anstieg haben.

d)  Ermittle diejenige reelle Zahl , für die die Funktion mit und
an der Stelle stetig ist.
Untersuche, ob die Funktion für den gefundenen Wert auch differenzierbar ist.

a) Größtmöglichen Definitionsbereich bestimmen In der ersten Aufgabe ist eine Funktionenschar gegeben, die durch die Gleichung dargestellt wird. Der Parameter gehört zur Menge der rationalen Zahlen und ist echt größer als Null. Der Definitionsbereich gibt alle Werte an, für die die Funktion definiert ist, die man also in den Funktionsterm einsetzen darf. Nicht definiert sind die Funktionen dann, wenn das Argument der -Funktion einen negativen Wert annimmt. Es muss also gelten: Daraus ergibt sich der Definitionsbereich . Wertebereich bestimmen Der Wertebereich einer Funktion sind alle -Werte, die die Funktion annimmt. Für die Funktionenschar gilt also: . Nullstellen berechnen Nullstellen sind die -Werte, an denen gilt. Um diese zu bestimmen, musst du den Funktionsterm mit Null gleichsetzen. Die Nullstelle der Funktionenschar befindet sich bei . Schnittpunkte mit der -Achse Für den Schnittpunkt mit der -Achse muss gelten. Der Schnittpunkt mit der -Achse lautet somit . Gleichung der Asymptoten bestimmen Die senkrechte Asymptote befindet sich an der Stelle, an der die Funktion nicht definiert ist. Das ist der Fall für . Die senkrechte Asymptote hat somit die Gleichung: Entstehung des Graphen von und die lokalen Extremstellen Die Graphen der Funktionenschar gehen aus dem Graphen der Funktion durch eine Verschiebung um Einheiten in negative -Richtung hervor. Da der Graph der Logarithmusfunktion keine lokalen Extremstellen hat, besitzen auch die Graphen der Funktionenschar keine lokalen Extremstellen. 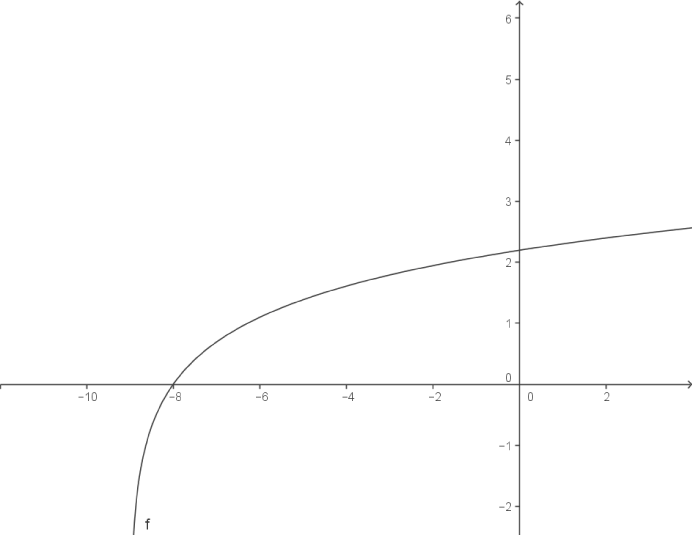Zeichnung des Graphen Zeichne dir die senkrechte Asymptote, sowie die Nullstelle und den Schnittpunkt mit der -Achse ein um den Graphen zu zeichnen.

b) Zeige, dass eine Stammfunktion ist Du sollst zeigen, dass eine Stammfunktion zu ist. Dafür musst du zeigen, dass die Ableitung von gerade der Funktion entspricht. Für die Ableitung von benötigst du die Produktregel. Daraus folgt, dass eine Stammfunktion von darstellt. Flächeninhalt berechnen 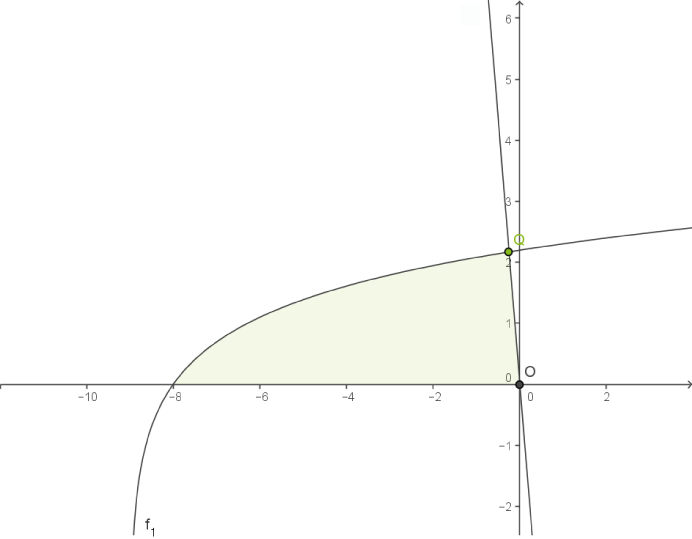Du sollst den Flächeninhalt der grün eingefärbten Fläche berechnen. Für den Bereich wird die Fläche vom Graphen der Funktion und durch die -Achse begrenzt. Im Bereich wird die Fläche durch und die -Achse begrenzt. Beginne mit der Fläche , die vom Graphen begrenzt wird. Du hast gezeigt, dass eine Stammfunktion von ist, du kannst die Fläche also folgendermaßen berechnen: Die Fläche ist ein rechtwinkliges Dreieck mit Schenkellänge und . Den gesuchten Flächeninhalt berechnest du, indem du die Flächen und addierst. Der Inhalt der Fläche beträgt ungefähr FE.   Formel für minimalen Abstand zum Koordinatenursprung Du sollst eine Gleichung aufstellen, die den Abstand der Punkte auf dem Graphen zum Koordinatenursprung beschreibt. Wenn du diese minimierst, erhältst du die Kordinate des Punktes mit minimalem Abstand zum Koordinatenursprung. Der Abstand eines Punktes auf und dem Koordinatenursprung lässt sich mit dem Satz von Pythagoras berechnen. Es gilt außerdem Die Gleichung der Zielfunktionen lautet .

c) Stelle mit gleichem Anstieg bestimmen Du sollst die Stelle bestimmen, an der der Graph und der Graph von den gleichen Anstieg haben. An dieser Stelle müssen also die Ableitungen der beiden Funktionen identisch sein. Bilde die Ableitungen und löse die Gleichung nach auf. Die quadratische Gleichung kannst du mit der p-q-Formel lösen. Da liegt sie nicht im Definitionsbereich der Funktion . Die Stelle an der die Graphen der beiden Funktionen den gleichen Anstieg haben ist somit .

d) Stetigkeit Du sollst den Parameter bestimmen, für den die Funktion an der Stelle stetig ist. Damit eine Funktion stetig ist müssen zunächst die Funktionswerte an der Stelle übereinstimmen. Es muss also gelten: Für stimmen die Funktionswert für überein. Zu überprüfen bleibt, ob der Grenzwert für existiert. Der Grenzwert existiert und somit ist die Funktion für stetig in .   Differenzierbarkeit Nun sollst du prüfen, ob für das eben berechnete die Funktion auch differenzierbar ist. Leite die Funktion zunächst stückweise ab Du musst also prüfen ob folgende Grenzwerte existieren und die Gleichung erfüllen: Die Grenzwerte stimmen nicht überein, somit ist die Funktion nicht differenzierbar in .