Pflichtaufgabe 2 - Analytische Geometrie
In einem kartesischen Koordinatensystem sind die Punkte  ,
,  und
und  gegeben.
a)
Durch die Punkte
gegeben.
a)
Durch die Punkte  ,
,  und
und  ist eindeutig eine Ebene
ist eindeutig eine Ebene  bestimmt.
bestimmt.
Ermitteln Sie die Koordinaten eines Punktes , so dass das Viereck
, so dass das Viereck  ein Parallelogramm ist und berechnen Sie die Maßzahl des Flächeninhalts dieses Parallelogramms.
Ermitteln Sie eine Koordinatengleichung der Ebene
ein Parallelogramm ist und berechnen Sie die Maßzahl des Flächeninhalts dieses Parallelogramms.
Ermitteln Sie eine Koordinatengleichung der Ebene  .
Die Ebene
.
Die Ebene  schneidet die
schneidet die  -Ebene des Koordinatensystems in einer Geraden
-Ebene des Koordinatensystems in einer Geraden  .
.
Erklären Sie, warum diese Gerade eine durch den Koordinatenursprung verlaufende Gerade sein muss und ermitteln Sie eine Parametergleichung dieser Geraden
eine durch den Koordinatenursprung verlaufende Gerade sein muss und ermitteln Sie eine Parametergleichung dieser Geraden  .
Berechnen Sie das Gradmaß des Winkels, unter dem die Ebene
.
Berechnen Sie das Gradmaß des Winkels, unter dem die Ebene  die
die  -Ebene des Koordinatensystems schneidet.
b)
-Ebene des Koordinatensystems schneidet.
b)
 der Ebene
der Ebene  berührt und berechnen Sie die Maßzahl des Radius der Kugel.
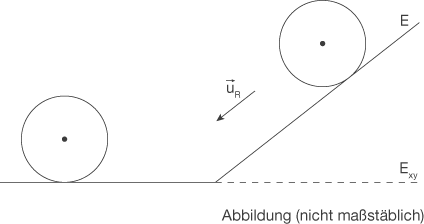
Wenn die Kugel nicht mehr gehalten wird, rollt diese auf dem kürzesten Weg auf die horizontale Platte zu.
Ermitteln Sie die Koordinaten eines Vektors
berührt und berechnen Sie die Maßzahl des Radius der Kugel.
Wenn die Kugel nicht mehr gehalten wird, rollt diese auf dem kürzesten Weg auf die horizontale Platte zu.
Ermitteln Sie die Koordinaten eines Vektors  , der die Bewegungsrichtung des Mittelpunktes der Kugel während dieses Rollens beschreibt.
Beim Auftreffen auf der horizontalen Platte berührt die Kugel diese in einem Punkt
, der die Bewegungsrichtung des Mittelpunktes der Kugel während dieses Rollens beschreibt.
Beim Auftreffen auf der horizontalen Platte berührt die Kugel diese in einem Punkt  der
der  -Ebene.
-Ebene.
Berechnen Sie die Koordinaten dieses Punktes .
.
Ermitteln Sie die Koordinaten eines Punktes
Erklären Sie, warum diese Gerade

Eine horizontale Platte und eine dazu geneigte Platte bilden eine Versuchsanordnung zum Abrollen einer Kugel. Im kartesischen Koordinatensystem seien die Lage der horizontalen Platte durch die  -Ebene und die Lage der geneigten Platte durch die Ebene
-Ebene und die Lage der geneigten Platte durch die Ebene  oberhalb der
oberhalb der  -Ebene beschrieben.
-Ebene beschrieben.
Eine Kugel berührt die geneigte Platte und wird zunächst festgehalten.
In dieser Ausgangsposition ist der Punkt der Mittelpunkt der Kugel.
der Mittelpunkt der Kugel.
Zeigen Sie, dass die Kugel in der Ausgangsposition die geneigte Platte im Punkt Eine Kugel berührt die geneigte Platte und wird zunächst festgehalten.
In dieser Ausgangsposition ist der Punkt
Berechnen Sie die Koordinaten dieses Punktes
a)  Bestimme die Koordinaten des Punktes
Bestimme die Koordinaten des Punktes  Hier sollst du die Koordinaten des Punktes
Hier sollst du die Koordinaten des Punktes  so bestimmen, dass die Punkte
so bestimmen, dass die Punkte  ,
,  ,
,  und
und  ein Parallelogramm ergeben. Bei einem Parallelogramm sind die parallelen Seiten jeweils gleich lang. Das heißt, dass sie den gleichen Richtungsvektor haben.
Eine Skizze kann dir helfen, den Sachverhalt besser zu verstehen:
ein Parallelogramm ergeben. Bei einem Parallelogramm sind die parallelen Seiten jeweils gleich lang. Das heißt, dass sie den gleichen Richtungsvektor haben.
Eine Skizze kann dir helfen, den Sachverhalt besser zu verstehen:
 Du kannst erkennen, dass du den Ortsvektor des Punktes
Du kannst erkennen, dass du den Ortsvektor des Punktes  durch folgende geometrische Operation darstellen kannst:
durch folgende geometrische Operation darstellen kannst: 
![\(\begin{array}{rllll}
\overrightarrow{OD}&=&\overrightarrow{OA}+\overrightarrow{BC}\\[5pt]
&=&\begin{pmatrix}1\\1\\4\end{pmatrix}+\left(\begin{pmatrix}-1\\3\\4\end{pmatrix}-\begin{pmatrix}3\\2\\10\end{pmatrix}\right)\\[5pt]
&=&\begin{pmatrix}1\\1\\4\end{pmatrix}+\begin{pmatrix}-4\\1\\-6\end{pmatrix}\\[5pt]
&=&\begin{pmatrix}-3\\2\\-2\end{pmatrix}\\
\end{array}\)](https://www.schullv.de/resources/formulas/160d796380ef13d1a03a14011ee6ba98c87ee7679b58776f2584b8a7a4715674_light.svg) Der Punkt
Der Punkt  hat die Koordinaten
hat die Koordinaten  .
.
 Berechne die Maßzahl des Flächeninhalts
Berechne die Maßzahl des Flächeninhalts  Bei der Berechnung des Flächeninhalts
Bei der Berechnung des Flächeninhalts  hast du ebenfalls zwei verschieden Möglichkeiten. Du kannst den Flächeninhalt
hast du ebenfalls zwei verschieden Möglichkeiten. Du kannst den Flächeninhalt  mit Hilfe des Vektorprodukts berechnen (Lösungsweg A) oder mit der Flächeninhaltsformel für ein Parallelogramm (Lösungsweg B).
mit Hilfe des Vektorprodukts berechnen (Lösungsweg A) oder mit der Flächeninhaltsformel für ein Parallelogramm (Lösungsweg B).
 Lösungsweg A: Vektorprodukt
Die Fläche eines Parallelogramm kannst du mit Hilfe folgender Formel berechnen:
Lösungsweg A: Vektorprodukt
Die Fläche eines Parallelogramm kannst du mit Hilfe folgender Formel berechnen:
 Dabei sind die Vektoren
Dabei sind die Vektoren  und
und  die Richtungsvektoren, die das Parallelogramm aufspannen.
die Richtungsvektoren, die das Parallelogramm aufspannen.
![\(\begin{array}{rllll}
A&=&|\overrightarrow{AB}\times\overrightarrow{AC}|\\[5pt]
&=&\left|\left(\begin{pmatrix}3\\2\\10\end{pmatrix}-\begin{pmatrix}1\\1\\4\end{pmatrix}\right)\times\left(\begin{pmatrix}-1\\3\\4\end{pmatrix}-\begin{pmatrix}1\\1\\4\end{pmatrix}\right)\right|=\left|\begin{pmatrix}2\\1\\6\end{pmatrix}\times\begin{pmatrix}-2\\2\\0\end{pmatrix}\right|\\[5pt]
&=&\left|\begin{pmatrix}1\cdot0&-&6\cdot2\\6\cdot(-2)&-&2\cdot0\\2\cdot2&-&1\cdot(-2)\end{pmatrix}\right|=\left|\begin{pmatrix}-12\\-12\\6\end{pmatrix}\right|\\[5pt]
&=&\sqrt{(-12)^2+(-12)^2+6^2}=\sqrt{324}\\[5pt]
&=&18\\
\end{array}\)](https://www.schullv.de/resources/formulas/16c724ca3034cedfa828fdf9a591cfa68725cb3386824e530437f5fe8fa2e820_light.svg) Der Flächeninhalt des Parallelogramms
Der Flächeninhalt des Parallelogramms  hat die Maßzahl
hat die Maßzahl  .
.
 Lösungsweg B: Flächeninhaltsformel
Den Flächeninhalt eines Parallelogramms berechnest du mit folgender Formel:
Lösungsweg B: Flächeninhaltsformel
Den Flächeninhalt eines Parallelogramms berechnest du mit folgender Formel:
 Dabei entspricht das
Dabei entspricht das  einer Seite des Parallelogramms und
einer Seite des Parallelogramms und  dem Abstand der parallelen Seiten. Das
dem Abstand der parallelen Seiten. Das  entspricht in diesem Fall zum Beispiel der Länge der Strecke
entspricht in diesem Fall zum Beispiel der Länge der Strecke  . Um diese zu bestimmen, berechnest du den Abstand zwischen den Punkten
. Um diese zu bestimmen, berechnest du den Abstand zwischen den Punkten  und
und  . Den Abstand zwischen zwei Punkten
. Den Abstand zwischen zwei Punkten  und
und  berechnest du mit folgender Formel:
berechnest du mit folgender Formel:
 Die Höhe
Die Höhe  entspricht dem Abstand des Punktes
entspricht dem Abstand des Punktes  zu der Geraden durch die Punkte
zu der Geraden durch die Punkte  und
und  , da es sich um parallele Seiten handelt. Den Abstand eines Punktes
, da es sich um parallele Seiten handelt. Den Abstand eines Punktes  zu einer Geraden
zu einer Geraden  berechnest du wie folgt:
berechnest du wie folgt:
 Gehe nun folgendermaßen vor:
Gehe nun folgendermaßen vor:
 Setze die Koordinaten der Punkte
Setze die Koordinaten der Punkte  und
und  in die Formel zur Berechung des Abstands ein.
in die Formel zur Berechung des Abstands ein.
 Der Abstand
Der Abstand  zwischen den Punkten
zwischen den Punkten  und
und  beträgt
beträgt  LE.
2. Schritt: Berechne die Höhe
LE.
2. Schritt: Berechne die Höhe  Die Höhe
Die Höhe  entspricht dem Abstand des Punktes
entspricht dem Abstand des Punktes  zu der Geraden durch die Punkte
zu der Geraden durch die Punkte  und
und  . Du benötigst den Richtungsvektor
. Du benötigst den Richtungsvektor  der Gerade, damit du diesen in die Formel zur Berechnung des Abstands einsetzen kannst. Dieser Richtungsvektor
der Gerade, damit du diesen in die Formel zur Berechnung des Abstands einsetzen kannst. Dieser Richtungsvektor  der Gerade
der Gerade  entspricht dem Vektor
entspricht dem Vektor  . Diesen hast du schon berechnet. Es gilt:
. Diesen hast du schon berechnet. Es gilt:  . Als Stützpunkt kannst du den Punkt
. Als Stützpunkt kannst du den Punkt  wählen. So erhältst du folgende Geradengleichung für die Gerade durch die Punkte
wählen. So erhältst du folgende Geradengleichung für die Gerade durch die Punkte  und
und  :
:
 Nun kannst du die Werte in die Formel einsetzen.
Nun kannst du die Werte in die Formel einsetzen.
![\(\begin{array}{rllll}
h_a&=&\dfrac{\left|\left(\overrightarrow{p}-\overrightarrow{a}\right)\times\overrightarrow{u}\right|}{|\overrightarrow{u}|}=\dfrac{\left|\left(\overrightarrow{OA}-\overrightarrow{OC}\right)\times\overrightarrow{u}\right|}{|\overrightarrow{u}|}\\[5pt]
&=&\dfrac{\left|\begin{pmatrix}2\\-2\\0\end{pmatrix}\times\begin{pmatrix}2\\1\\6\end{pmatrix}\right|}{\sqrt{2^1+1^2+6^2}}=\dfrac{\left|\begin{pmatrix}-2\cdot6&-&0\cdot1\\0\cdot2&-&2\cdot6\\2\cdot1&-&(-2)\cdot2\end{pmatrix}\right|}{\sqrt{4+1+36}}=\dfrac{\left|\begin{pmatrix}-12\\-12\\6\end{pmatrix}\right|}{\sqrt{41}}\\[5pt]
&=&\dfrac{\sqrt{(-12)^2+(-12)^2+6^2}}{\sqrt{41}}=\dfrac{\sqrt{324}}{\sqrt{41}}=\dfrac{18}{\sqrt{41}}\\
\end{array}\)](https://www.schullv.de/resources/formulas/837aab6e070d3b67da00066d5e4c0101607453682a8bb7f672434f05e0112e94_light.svg) Die Höhe
Die Höhe  beträgt
beträgt  .
3. Schritt: Berechne den Flächeninhalt
.
3. Schritt: Berechne den Flächeninhalt  Nun kannst du den Abstand
Nun kannst du den Abstand  und die Höhe
und die Höhe  in die Formel zur Berechnung des Flächeninhalts einsetzen.
in die Formel zur Berechnung des Flächeninhalts einsetzen.
 Der Flächeninhalt
Der Flächeninhalt  des Parallelogramms
des Parallelogramms  hat die Maßzahl
hat die Maßzahl  .
.
 Ermittle eine Koordinatengleichung der Ebene
Ermittle eine Koordinatengleichung der Ebene  Durch die Punkte
Durch die Punkte  ,
,  und
und  ist eine Ebene
ist eine Ebene  bestimmt.
Du sollst eine Koordinatengleichung dieser Ebene bestimmen.
Die Koordinatengleichung einer Ebene sieht folgendermaßen aus:
bestimmt.
Du sollst eine Koordinatengleichung dieser Ebene bestimmen.
Die Koordinatengleichung einer Ebene sieht folgendermaßen aus:
 mit
mit
 zu ermitteln.
Lösungsweg B: Aus der Parameterform der Ebene kannst du alternativ ein Lineares Gleichungssystem (LGS) aufstellen und die beiden Parameter, die darin enthalten sind, eliminieren.
Lösungsweg C: Du berechnest aus der Parameterform der Ebene den Normalenvektor über ein Lineares Gleichungssystem (LGS), das du mit Hilfe der Richtungsvektoren aufstellst. Anschließend wählst du für eine Koordinate einen beliebigen Wert, um die anderen beiden Koordinaten über das LGS zu berechnen. Um den Parameter
zu ermitteln.
Lösungsweg B: Aus der Parameterform der Ebene kannst du alternativ ein Lineares Gleichungssystem (LGS) aufstellen und die beiden Parameter, die darin enthalten sind, eliminieren.
Lösungsweg C: Du berechnest aus der Parameterform der Ebene den Normalenvektor über ein Lineares Gleichungssystem (LGS), das du mit Hilfe der Richtungsvektoren aufstellst. Anschließend wählst du für eine Koordinate einen beliebigen Wert, um die anderen beiden Koordinaten über das LGS zu berechnen. Um den Parameter  zu ermitteln, setzt du einen der gegebenen Punkte in die Koordinatengleichung ein.
zu ermitteln, setzt du einen der gegebenen Punkte in die Koordinatengleichung ein.
 Lösungsweg A: Koordinatengleichung über Vektorprodukt
Um das Vektorprodukt zu bilden, benötigst du die Parameterform der Ebene, die du im 1. Schritt aufstellst.
Da der Normalenvektor einer Ebene auch senkrecht auf allen darin enthaltenen Vektoren steht, muss er folglich auch senkrecht auf den Richtungsvektoren der Parameterform stehen. Ermittle also im 2. Schritt den Normalenvektor der Ebene über das Vektorprodukt der beiden Richtungsvektoren.
Im 3. Schritt erstellst du die Koordinatengleichung und setzt einen der gegebenen Punkte darin ein, um den Parameter
Lösungsweg A: Koordinatengleichung über Vektorprodukt
Um das Vektorprodukt zu bilden, benötigst du die Parameterform der Ebene, die du im 1. Schritt aufstellst.
Da der Normalenvektor einer Ebene auch senkrecht auf allen darin enthaltenen Vektoren steht, muss er folglich auch senkrecht auf den Richtungsvektoren der Parameterform stehen. Ermittle also im 2. Schritt den Normalenvektor der Ebene über das Vektorprodukt der beiden Richtungsvektoren.
Im 3. Schritt erstellst du die Koordinatengleichung und setzt einen der gegebenen Punkte darin ein, um den Parameter  zu ermitteln.
Parameterform der Ebene:
zu ermitteln.
Parameterform der Ebene:

 wählen und als Richtungsvektoren die Vektoren
wählen und als Richtungsvektoren die Vektoren  und
und  .
.
 2. Schritt: Normalenvektor ermitteln
Der Normalenvektor
2. Schritt: Normalenvektor ermitteln
Der Normalenvektor  ergibt sich durch das Vektorprodukt der beiden Richtungsvektoren:
ergibt sich durch das Vektorprodukt der beiden Richtungsvektoren:
 Wir rechnen daher:
Wir rechnen daher:
 Ein Normalenvektor muss immer senkrecht auf der Ebene stehen, die Länge des Vektors spielt dabei allerdings keine Rolle. Daher kannst du den Vektor mit dem Faktor
Ein Normalenvektor muss immer senkrecht auf der Ebene stehen, die Länge des Vektors spielt dabei allerdings keine Rolle. Daher kannst du den Vektor mit dem Faktor  kürzen:
kürzen:
 3. Schritt: Koordinatengleichung bestimmen
Jetzt kannst du den Normalenvektor in die Koordinatengleichung der Ebene einsetzen:
3. Schritt: Koordinatengleichung bestimmen
Jetzt kannst du den Normalenvektor in die Koordinatengleichung der Ebene einsetzen:
 Um den Parameter
Um den Parameter  zu ermitteln, kannst du beispielsweise den Punkt
zu ermitteln, kannst du beispielsweise den Punkt  in die Gleichung einsetzen:
in die Gleichung einsetzen:
 Eine Koordinatengleichung der Ebene E lautet:
Eine Koordinatengleichung der Ebene E lautet: 
 Lösungsweg B: Koordinatengleichung über Parameterform und LGS
Die Parameterform der Ebene bestimmst du wie in Lösungsweg A beschrieben.
Lösungsweg B: Koordinatengleichung über Parameterform und LGS
Die Parameterform der Ebene bestimmst du wie in Lösungsweg A beschrieben.
 Daraus kannst du dann folgendes lineares Gleichungssystem aufstellen, indem du die Komponenten zeilenweise abliest:
Daraus kannst du dann folgendes lineares Gleichungssystem aufstellen, indem du die Komponenten zeilenweise abliest:
 Wir erhalten genau dasselbe Ergebnis wie in Lösungsweg A:
Wir erhalten genau dasselbe Ergebnis wie in Lösungsweg A: 
 Lösungsweg C: Normalenvektor ohne Vektorprodukt
Du suchst einen Vektor, der senkrecht auf der Ebene
Lösungsweg C: Normalenvektor ohne Vektorprodukt
Du suchst einen Vektor, der senkrecht auf der Ebene  steht. Dazu nutzt du hier das Skalarprodukt. Wenn zwei Vektoren senkrecht aufeinander stehen, nimmt ihr Skalarprodukt den Wert Null an.
steht. Dazu nutzt du hier das Skalarprodukt. Wenn zwei Vektoren senkrecht aufeinander stehen, nimmt ihr Skalarprodukt den Wert Null an.
Also multiplizierst du jeweils den Normalenvektor mit den beiden Stützvektoren:
mit den beiden Stützvektoren:

 Damit erhältst du das lineare Gleichungssystem:
Damit erhältst du das lineare Gleichungssystem:
 Da es unendlich viele Normalenvektoren gibt, die diese Eigenschaften erfüllen, kann einer der Parameter beliebig gewählt werden.
Da es unendlich viele Normalenvektoren gibt, die diese Eigenschaften erfüllen, kann einer der Parameter beliebig gewählt werden.
In der zweiten Gleichung stehen bereits nur 2 unbekannte Koordinaten, also ist es sinnvoll einen der beiden beliebig zu wählen. Zum Beispiel :
:
 Jetzt kannst du Gleichung
Jetzt kannst du Gleichung  nach
nach  auflösen und anschließend in Gleichung
auflösen und anschließend in Gleichung  einsetzen:
einsetzen:
 In Gleichung
In Gleichung  einsetzen:
einsetzen:
 Somit erhältst du den Normalenvektor:
Somit erhältst du den Normalenvektor:  Diesen kannst du wiederum in die Koordinatengleichung einsetzen und den Parameter
Diesen kannst du wiederum in die Koordinatengleichung einsetzen und den Parameter  ermitteln.
ermitteln.
 Um den Parameter
Um den Parameter  zu ermitteln, kannst du einen der drei gegebenen Punkte, zum Beispiel den Punkt
zu ermitteln, kannst du einen der drei gegebenen Punkte, zum Beispiel den Punkt  , in die Gleichung einsetzen:
, in die Gleichung einsetzen:
 Wir erhalten genau dasselbe Ergebnis wie in Lösungsweg A:
Wir erhalten genau dasselbe Ergebnis wie in Lösungsweg A: 
 Begründe den Verlauf der Geraden
Begründe den Verlauf der Geraden  Die Ebene
Die Ebene  schneidet sich mit der
schneidet sich mit der  -Ebene in der Geraden
-Ebene in der Geraden  . Du sollst nun begründen, warum die Gerade
. Du sollst nun begründen, warum die Gerade  durch den Ursprung verlaufen muss.
Die
durch den Ursprung verlaufen muss.
Die  -Ebene hat folgende Koordinatengleichung:
-Ebene hat folgende Koordinatengleichung:
 Berechne nun die Schnittgerade der beiden Ebenen. Setze dazu die ermittelten Gleichungen gleich. Du erhältst folgendes Gleichungssystem:
Berechne nun die Schnittgerade der beiden Ebenen. Setze dazu die ermittelten Gleichungen gleich. Du erhältst folgendes Gleichungssystem:
 Setzt du Gleichung
Setzt du Gleichung  in Gleichung
in Gleichung  ein und multiplizierst mit
ein und multiplizierst mit  , so erhältst du folgende Gleichung der Schnittgeraden:
, so erhältst du folgende Gleichung der Schnittgeraden:
 Diese Gleichung ist erfüllt, wenn sowohl das
Diese Gleichung ist erfüllt, wenn sowohl das  , als auch das
, als auch das  den Wert Null haben. Die Gerade
den Wert Null haben. Die Gerade  geht demnach durch den Ursprung.
geht demnach durch den Ursprung.
 Parametergleichung der Geraden
Parametergleichung der Geraden  Die zuvor bestimmte Ebene
Die zuvor bestimmte Ebene  schneidet die
schneidet die  -Ebene des Koordinatensystems in einer Geraden
-Ebene des Koordinatensystems in einer Geraden  , die durch den Koordinatenursprung verläuft. Du sollst die Gleichung dieser Geraden
, die durch den Koordinatenursprung verläuft. Du sollst die Gleichung dieser Geraden  in Parameterform bestimmen.
Die Schnittgerade der Ebene
in Parameterform bestimmen.
Die Schnittgerade der Ebene  mit der
mit der  -Ebene erhältst du, indem du ein lineares Gleichungssystem aus der Parameterform der Ebene
-Ebene erhältst du, indem du ein lineares Gleichungssystem aus der Parameterform der Ebene  aufstellst und für
aufstellst und für  den Wert Null einsetzt. Parameterform der Ebene
den Wert Null einsetzt. Parameterform der Ebene  :
:
 Somit erhältst du folgendes LGS:
Somit erhältst du folgendes LGS:
 Du suchst die Schnittgerade mit der
Du suchst die Schnittgerade mit der  -Ebene. Für die
-Ebene. Für die  -Ebene gilt:
-Ebene gilt:  . Das kannst du nun in Gleichung
. Das kannst du nun in Gleichung  deines LGS einsetzen und erhältst einen Wert für den Parameter
deines LGS einsetzen und erhältst einen Wert für den Parameter  , den du wiederum in die Parameterform der Ebene
, den du wiederum in die Parameterform der Ebene  einsetzt. Somit erhältst du die Geradengleichung der Schnittgerade
einsetzt. Somit erhältst du die Geradengleichung der Schnittgerade  :
:

 in die Ebenengleichung
in die Ebenengleichung  eingesetzt:
eingesetzt:
![\(\begin{array}{rllll}
s: \vec{x} &=& \begin{pmatrix}1\\1\\4\end{pmatrix} + \left(-\frac{2}{3}\right) \cdot \begin{pmatrix}2\\1\\6\end{pmatrix} + n \cdot \begin{pmatrix}-2\\2\\0\end{pmatrix}&\scriptsize \\[5pt]
s: \vec{x} &=& \begin{pmatrix}1\\1\\4\end{pmatrix} - \begin{pmatrix}\frac{4}{3}\\\frac{2}{3}\\4\end{pmatrix} + n \cdot \begin{pmatrix}-2\\2\\0\end{pmatrix}&\scriptsize \\[5pt]
s: \vec{x} &=& \begin{pmatrix}-\frac{1}{3}\\\frac{1}{3}\\0\end{pmatrix} + n \cdot \begin{pmatrix}-2\\2\\0\end{pmatrix}&\scriptsize \\
\end{array}\)](https://www.schullv.de/resources/formulas/3d7ac8c5fdaaa22253db3c767d01991880ae47508e138c777c13ad4bed79927b_light.svg) Eine Parametergleichung der Geraden
Eine Parametergleichung der Geraden  lautet:
lautet:

 Schnittwinkel
Schnittwinkel  der Ebene
der Ebene  und der
und der  -Ebene
Den Schnittwinkel
-Ebene
Den Schnittwinkel  zwischen zwei Ebenen berechnest du mit folgender Formel:
zwischen zwei Ebenen berechnest du mit folgender Formel:
 Die Koordinatengleichung der Ebene
Die Koordinatengleichung der Ebene  hast du zuvor ermittelt mit:
hast du zuvor ermittelt mit:
 Aus dieser Koordinatengleichung kannst du den Normalenvektor
Aus dieser Koordinatengleichung kannst du den Normalenvektor  ablesen.
Es gilt:
ablesen.
Es gilt:
 Die
Die  -Ebene hat den Normalenvektor
-Ebene hat den Normalenvektor  .
Setze nun die Vektoren
.
Setze nun die Vektoren  und
und  in die Formel zur Winkelberechnung ein.
in die Formel zur Winkelberechnung ein.
![\(\begin{array}{rllll}
\cos\phi&=&\dfrac{|\overrightarrow{n_E}\cdot\overrightarrow{n_{xy}}|}{|\overrightarrow{n_E}|\cdot|\overrightarrow{n_{xy}}|}\\[5pt]
\cos\phi&=&\dfrac{\left|\begin{pmatrix}-2\\-2\\1\end{pmatrix}\cdot\begin{pmatrix}0\\0\\1\end{pmatrix}\right|}{\left|\begin{pmatrix}-2\\-2\\1\end{pmatrix}\right|\cdot\left|\begin{pmatrix}0\\0\\1\end{pmatrix}\right|}\\[5pt]
\cos\phi&=&\dfrac{\left|(-2)\cdot0+(-2)\cdot0+1\cdot1\right|}{\sqrt{(-2)^2+(-2)^2+\left(1\right)^2}\cdot\sqrt{0^2+0^2+1^2}}\\[5pt]
\cos\phi&=&\dfrac{1}{\sqrt{4+4+1}\cdot\sqrt{1}}\\[5pt]
\cos\phi&=&\dfrac{1}{\sqrt{9}\cdot1}\\[5pt]
\cos\phi&=&\frac{1}{3}&\scriptsize \mid\; cos^{-1}\\[5pt]
\phi&=&70,5^{\circ}\\
\end{array}\)](https://www.schullv.de/resources/formulas/9e425e19bce077ab16048f4207b6bd35f4d0e298e384de90310ea2b4d7ca5329_light.svg) Der Winkel mit dem die Ebene
Der Winkel mit dem die Ebene  die
die  -Ebene schneidet beträgt
-Ebene schneidet beträgt  .
.

- Berechne den Abstand
.
- Berechne die Höhe
.
- Setze diese Werte in die Formel zur Berechnung des Flächeninhalts ein.
: Normalenvektor der Ebene E, ein Vektor der senkrecht auf der Ebene steht
: Konstante
,
: Richtungsvektoren, die die Ebene aufspannen
: Stützvektor (Ortsvektor eines Punktes
, der in der Ebene liegt)
Also multiplizierst du jeweils den Normalenvektor
In der zweiten Gleichung stehen bereits nur 2 unbekannte Koordinaten, also ist es sinnvoll einen der beiden beliebig zu wählen. Zum Beispiel
b)  Zeige, dass der Punkt
Zeige, dass der Punkt  dem Berührpunkt entspricht
In dieser Teilaufgabe sollst du zeigen, dass die Kugel in der Ausgangsposition mit dem Mittelpunkt
dem Berührpunkt entspricht
In dieser Teilaufgabe sollst du zeigen, dass die Kugel in der Ausgangsposition mit dem Mittelpunkt  die Ebene
die Ebene  in dem Punkt
in dem Punkt  berührt.
Stelle dazu zunächst eine Lotgerade
berührt.
Stelle dazu zunächst eine Lotgerade  durch den Punkt
durch den Punkt  zu der Ebene
zu der Ebene  auf. Berechne dann im 2. Schritt den Schnittpunkt der Geraden
auf. Berechne dann im 2. Schritt den Schnittpunkt der Geraden  und der Ebene
und der Ebene  .
1. Schritt: Aufstellen der Lotgeraden
.
1. Schritt: Aufstellen der Lotgeraden  Die Lotgerade
Die Lotgerade  steht senkrecht auf der Ebene
steht senkrecht auf der Ebene  . Das bedeutet, dass der Richtungsvektor der Geraden dem Normalenvektor der Ebene
. Das bedeutet, dass der Richtungsvektor der Geraden dem Normalenvektor der Ebene  entspricht. Dieser lautet:
entspricht. Dieser lautet:
 Der Punkt
Der Punkt  dient als Stützpunkt der Geraden. Nun kannst du eine Geradengleichung der Lotgerade
dient als Stützpunkt der Geraden. Nun kannst du eine Geradengleichung der Lotgerade  aufstellen.
aufstellen.
![\(\begin{array}{rl}
g:\overrightarrow{x}&=&\overrightarrow{OM}+t\cdot\overrightarrow{n}\\[5pt]
g:\overrightarrow{x}&=&\begin{pmatrix}-1\\-2\\12\end{pmatrix}+t\cdot \begin{pmatrix}-2\\-2\\1\end{pmatrix}\\
\end{array}\)](https://www.schullv.de/resources/formulas/c6ec627f5fc9a4ca4a3c6db5e1b8b79bec2aac44deb1b5f4b3f652ee8004457e_light.svg) 2. Schritt: Berechne den Schnittpunkt
Um nun den Schnittpunkt der Lotgerade
2. Schritt: Berechne den Schnittpunkt
Um nun den Schnittpunkt der Lotgerade  und der Ebenen
und der Ebenen  zu berechnen, setzt du die Einträge der Lotgerade komponentenweise in die Koordinatengleichung der Ebene
zu berechnen, setzt du die Einträge der Lotgerade komponentenweise in die Koordinatengleichung der Ebene  ein.
Die Koordinatengleichung der Ebene
ein.
Die Koordinatengleichung der Ebene  hast du zuvor ermittelt mit:
hast du zuvor ermittelt mit:
 Einsetzen der Einträge:
Einsetzen der Einträge:
 Diesen Wert
Diesen Wert  kannst du nun in die Geradengleichung
kannst du nun in die Geradengleichung  einsetzen, damit du den Schnittpunkt erhältst.
einsetzen, damit du den Schnittpunkt erhältst.
![\(\begin{array}{rllll}
g:\overrightarrow{x}&=&\begin{pmatrix}-1\\-2\\12\end{pmatrix}+t\cdot\begin{pmatrix}-2\\-2\\1\end{pmatrix}&\scriptsize \text{Einsetzen von t}\\[5pt]
\overrightarrow{x}&=&\begin{pmatrix}-1\\-2\\12\end{pmatrix}-2\cdot \begin{pmatrix}-2\\-2\\1\end{pmatrix}\\[5pt]
\overrightarrow{x}&=&\begin{pmatrix}-1\\-2\\12\end{pmatrix}+\begin{pmatrix}4\\4\\-2\end{pmatrix}\\[5pt]
\overrightarrow{x}&=&\begin{pmatrix}3\\2\\10\end{pmatrix}\\
\end{array}\)](https://www.schullv.de/resources/formulas/b6452e4c4854c9db30acdb3c2df009ba4ab1de96a7080fc039d6134f8f1c64b5_light.svg) Das liefert dir den Ortsvektor zum Punkt
Das liefert dir den Ortsvektor zum Punkt  . Der Schnittpunkt hat die Koordinaten
. Der Schnittpunkt hat die Koordinaten  . Diese Koordinaten entsprechen den Koordinaten des Punktes
. Diese Koordinaten entsprechen den Koordinaten des Punktes  .
.
 Maßzahl des Radius der Kugel berechnen
Du hast eine Kugel gegeben, die auf einer geneigten Platte liegt, die durch die Ebene
Maßzahl des Radius der Kugel berechnen
Du hast eine Kugel gegeben, die auf einer geneigten Platte liegt, die durch die Ebene  oberhalb der
oberhalb der  -Ebene beschrieben wird und in Richtung des Vektors
-Ebene beschrieben wird und in Richtung des Vektors  auf die horizontale Platte zu rollt. Diese Kugel berührt die Ebene
auf die horizontale Platte zu rollt. Diese Kugel berührt die Ebene  im Punkt
im Punkt  und wird dort festgehalten. Ihr Mittelpunkt ist
und wird dort festgehalten. Ihr Mittelpunkt ist  .
.
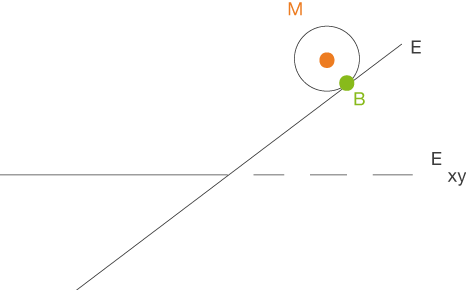 Du sollst die Maßzahl des Radius der Kugel bestimmen, die in diesem Fall dem Abstand der Punkte
Du sollst die Maßzahl des Radius der Kugel bestimmen, die in diesem Fall dem Abstand der Punkte  und
und  entspricht.
entspricht.
 Die Maßzahl des Radius der Kugel ist
Die Maßzahl des Radius der Kugel ist  .
.
 Ermittle die Koordinaten des Vektors
Ermittle die Koordinaten des Vektors  Die Kugel rollt nun auf dem kürzesten Weg auf die horizontale Platte zu. Überlege dir zunächst, was der kürzeste Weg ist und welche Bedingungen dafür gelten müssen.
Die Kugel rollt nun auf dem kürzesten Weg auf die horizontale Platte zu. Überlege dir zunächst, was der kürzeste Weg ist und welche Bedingungen dafür gelten müssen.
 .
1. Schritt: Parallelität zur Ebene
.
1. Schritt: Parallelität zur Ebene  Du kennst den Normalenvektor
Du kennst den Normalenvektor  der Ebene. Dieser lautet:
der Ebene. Dieser lautet:  Der Richtungsvektor
Der Richtungsvektor  , der die Bewegungsrichtung beschreibt, muss nun orthogonal zu dem Normalenvektor
, der die Bewegungsrichtung beschreibt, muss nun orthogonal zu dem Normalenvektor  stehen, damit er parallel zu der Ebene
stehen, damit er parallel zu der Ebene  ist. Das Skalarprodukt der beiden Vektoren muss demnach Null ergeben.
ist. Das Skalarprodukt der beiden Vektoren muss demnach Null ergeben.
![\(\begin{array}{rllll}
\overrightarrow{u_R}\circ\overrightarrow{n_E}&=&0\\[5pt]
\begin{pmatrix}x\\y\\z\end{pmatrix}\circ\begin{pmatrix}-2\\-2\\1\end{pmatrix}&=&0\\[5pt]
-2x-2y+1z&=&0\\
\end{array}\)](https://www.schullv.de/resources/formulas/314749c0131d0f657c57ff378531a1bb94dd92dad4bee78dfe70bb70ca2e0ccf_light.svg) 2. Schritt: Orthogonalität zur Schnittgeraden
2. Schritt: Orthogonalität zur Schnittgeraden  Der Richtungsvektor
Der Richtungsvektor  , der die Bewegungsrichtung beschreibt, muss nun orthogonal zu dem Richtungsvektor
, der die Bewegungsrichtung beschreibt, muss nun orthogonal zu dem Richtungsvektor  der Geraden
der Geraden  stehen, damit er auf dem kürzesten Weg auf die Ebene
stehen, damit er auf dem kürzesten Weg auf die Ebene  zu rollt. Das Skalarprodukt der beiden Vektoren muss demnach Null ergeben:
zu rollt. Das Skalarprodukt der beiden Vektoren muss demnach Null ergeben:
![\(\begin{array}{rllll}
\overrightarrow{u_R}\circ\overrightarrow{r}&=&0\\[5pt]
\begin{pmatrix}x\\y\\z\end{pmatrix}\circ\begin{pmatrix}-2\\2\\0\end{pmatrix}&=&0\\[5pt]
-2x+2y&=&0
\end{array}\)](https://www.schullv.de/resources/formulas/751eb48e56dbbc218f377f9c04b3c9db66636f4d11465d96a6e1d97f6d72efae_light.svg) 3. Schritt: Lineares Gleichungssystem lösen
Damit hast du nun 2 Bedingungen bestimmt und kann daraus ein lineares Gleichungssystem aufstellen:
3. Schritt: Lineares Gleichungssystem lösen
Damit hast du nun 2 Bedingungen bestimmt und kann daraus ein lineares Gleichungssystem aufstellen:
 Da 3 Variablen in 2 Gleichungen vorkommen, handelt es sich hier um ein unterbestimmtes Gleichungssystem. Wir können die Parameter
Da 3 Variablen in 2 Gleichungen vorkommen, handelt es sich hier um ein unterbestimmtes Gleichungssystem. Wir können die Parameter  und
und  in Abhängigkeit von
in Abhängigkeit von  angeben. Daher wählen wir nun eine beliebige Zahl für den Parameter
angeben. Daher wählen wir nun eine beliebige Zahl für den Parameter  , zum Beispiels
, zum Beispiels  . Dann erhalten für
. Dann erhalten für  und
und  :
:

 Koordinaten des Punktes P bestimmen
Die Kugel rollt, sobald sie losgelassen wird, auf dem kürzesten Weg in Richtung des Vektors
Koordinaten des Punktes P bestimmen
Die Kugel rollt, sobald sie losgelassen wird, auf dem kürzesten Weg in Richtung des Vektors
 auf die horizontale Platte zu, die durch die
auf die horizontale Platte zu, die durch die  -Ebene beschrieben wird.
-Ebene beschrieben wird.
Du sollst den Berührpunkt der Kugel mit der horizontalen Platte bestimmen.
der Kugel mit der horizontalen Platte bestimmen.
Dazu berechnest du zunächst die Koordinaten des Mittelpunktes der Kugel beim Auftreffen auf die -Ebene. Dazu kannst du eine Geradengleichung bestimmen, die den Weg des Mittelpunktes der Kugel beschreibt. Wähle als Ortsvektor den Mittelpunkt
-Ebene. Dazu kannst du eine Geradengleichung bestimmen, die den Weg des Mittelpunktes der Kugel beschreibt. Wähle als Ortsvektor den Mittelpunkt  und als Richtungsvektor den gegebenen Vektor
und als Richtungsvektor den gegebenen Vektor  .
Um nun die Koordinaten des Punktes
.
Um nun die Koordinaten des Punktes  zu erhalten, der den Kugelmittelpunkt zum Zeitpunkt des Auftreffens beschreibt, setzt du die horizontale Ebene um die Maßzahl des Radius der Kugel nach oben und berechnest den Schnittpunkt der Geraden mit der nach oben versetzten horizontalen Ebene.
zu erhalten, der den Kugelmittelpunkt zum Zeitpunkt des Auftreffens beschreibt, setzt du die horizontale Ebene um die Maßzahl des Radius der Kugel nach oben und berechnest den Schnittpunkt der Geraden mit der nach oben versetzten horizontalen Ebene.
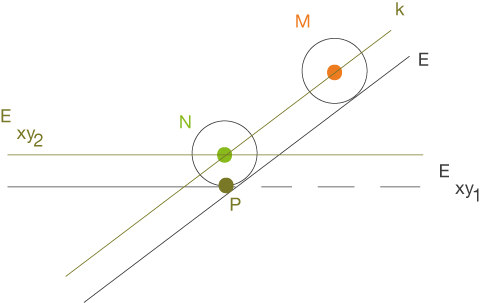 Den gesuchten Punkt
Den gesuchten Punkt  erhältst du, indem du die Koordinaten des Punktes
erhältst du, indem du die Koordinaten des Punktes  um den Betrag reduzierst, um den du die horizontale Ebene nach oben versetzt hast. Die Geradengleichung
um den Betrag reduzierst, um den du die horizontale Ebene nach oben versetzt hast. Die Geradengleichung  in Parameterform, die den Weg des Kugelmittelpunktes beschreibt, sieht folgendermaßen aus:
in Parameterform, die den Weg des Kugelmittelpunktes beschreibt, sieht folgendermaßen aus:
 Die horizontale Platte wird durch die
Die horizontale Platte wird durch die  -Ebene beschrieben. Eine Ebenengleichung in Koordinatenform ist:
-Ebene beschrieben. Eine Ebenengleichung in Koordinatenform ist:
 Die Ebene setzt du nun um die Maßzahl des Radius der Kugel nach oben. Die Maßzahl hat den Wert
Die Ebene setzt du nun um die Maßzahl des Radius der Kugel nach oben. Die Maßzahl hat den Wert  . Damit die Ebene horizontal bleibt, wird sie lediglich auf der
. Damit die Ebene horizontal bleibt, wird sie lediglich auf der  -Achse um den Wert
-Achse um den Wert  nach oben versetzt.
nach oben versetzt.
 Mit der zuvor bestimmten Parameterform der Geraden
Mit der zuvor bestimmten Parameterform der Geraden  kannst du ein LGS aufstellen:
kannst du ein LGS aufstellen:
 In Gleichung
In Gleichung  kannst du nun für
kannst du nun für  den entsprechenden Wert aus der Ebenengleichung
den entsprechenden Wert aus der Ebenengleichung  einsetzen:
einsetzen:
 Den soeben erhaltenen Wert für den Parameter
Den soeben erhaltenen Wert für den Parameter  kannst du nun in die Geradengleichung zu
kannst du nun in die Geradengleichung zu  einsetzen, um den Ortsvektor des Punktes
einsetzen, um den Ortsvektor des Punktes  zu bestimmen:
zu bestimmen:
 Um den Schnittpunkt zu ermitteln, hast du die Ebene
Um den Schnittpunkt zu ermitteln, hast du die Ebene  um den Wert
um den Wert  in
in  -Richtung nach oben versetzt. Die gesuchten Koordinaten des Punktes
-Richtung nach oben versetzt. Die gesuchten Koordinaten des Punktes  erhältst du also, indem du den ermittelten Punkt
erhältst du also, indem du den ermittelten Punkt  in
in  -Richtung um denselben Wert nach unten versetzt.
-Richtung um denselben Wert nach unten versetzt.
 Die Kugel berührt die
Die Kugel berührt die  -Ebene nach dem Abrollen über die geneigte Platte beim Auftreffen auf der horizontalen Platte im Punkt
-Ebene nach dem Abrollen über die geneigte Platte beim Auftreffen auf der horizontalen Platte im Punkt  .
.

- Rollt der Ball auf der Ebene
, so muss sich der Mittelpunkt parallel zu der Ebene
bewegen. Der Richtungsvektor
verläuft folglich senkrecht zum Normalenvektor der Ebene
. Bestimme also einen Vektor, der parallel zu der Ebene verläuft.
- Zuvor haben wir die Schnittgerade
der
-Ebene und der Ebene
aufgestellt. Da du hier den kürzesten Weg suchst, muss sich der Ball senkrecht auf die Schnittgerade zu bewegen.
- Stelle mit Hilfe der Bedingungen ein lineares Gleichungssystem auf und ermittle die Einträge des Vektors
.
Du sollst den Berührpunkt
Dazu berechnest du zunächst die Koordinaten des Mittelpunktes der Kugel beim Auftreffen auf die
