Wahlpflichtaufgabe 2 - Analytische Geometrie

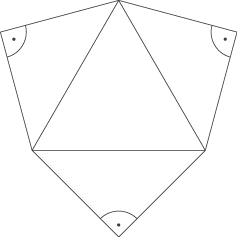
Geometrische Formen und Linien in einem symmetrischen Muster auf schwarzem Hintergrund.

Eine dreiseitige Pyramide werde von einem gleichseitigen Dreieck und drei zueinander kongruenten rechtwinklig-gleichschenkligen Dreiecken begrenzt.

Die nebenstehende Abbildung zeigt ein Netz einer solchen Pyramide.

Eine solche Pyramide sei in einem kartesischen Koordinatensystem des Raumes durch die Punkte $A$ , $B$ , $C$ und $D$ beschrieben. Das gleichseitige Dreieck $ABC$ beschreibe die Grundfläche und liege in der $xy$ -Ebene mit dem Punkt $A$ im Koordinatenursprung.
Außerdem sei der Punkt $B(a>0\mid 0\mid0)$ mit $a\in \mathbb{R}$ gegeben.
Von den Punkten $C$ und $D$ sei bekannt: $C(x_c\mid y_c>0\mid z_c)$ sowie $D(x_D\mid y_D\mid z_D>0)$ .

Begründen Sie, dass der Punkt $C$ die Koordinaten $x_c=\dfrac{a}{2}$ ; $y_c=\dfrac{a}{2}\sqrt{3}$ und $z_c=0$ hat.

Berechnen Sie die Koordinaten des Schnittpunktes der Seitenhalbierenden des Dreiecks $ABC$ sowie die Koordinaten des Punktes $D$ .

[Ergebnis zur Kontrolle: $D\left(\dfrac{a}{2}\mid \dfrac{a}{6}\sqrt{3}\mid \dfrac{a}{6}\sqrt{6}\right)$ ]

Zeigen Sie, dass die Größe des Winkels, den die Seitenkante $\overline{BD}$ mit der Grundfläche der Pyramide einschließt, unabhängig von $a$ ist.

$\blacktriangleright$ Begründe die Koordinaten des Punktes $\boldsymbol C$

Bei dieser Aufgabe hast du eine Pyramide $ABCD$ mit einem gleichseitigem Dreieck $ABC$ als Grundfläche gegeben. Diese liegt in der $\boldsymbol{xy}$ -Ebene. Der Punkt $A$ entspricht dem Koordinatenursprung und hat die Koordinaten $A(0\mid\;0\mid\;0)$ . Der Punkt $B$ hat die Koordinaten $B(a>0\mid\;0\mid\;0)$ . Du sollst nun begründen, warum der Punkt $C$ die Koordinaten $C\left(\frac{a}{2}\mid\;\frac{a}{2}\sqrt{3}\mid\;0\right)$ hat.

Überlege dir dazu, was für besondere Eigenschaften ein gleichseitiges Dreieck hat. Eine Skizze kann dir dabei helfen. Hier siehst du die $xy$ -Ebene in der Draufsicht:

Geometrische Darstellung eines Dreiecks mit den Punkten A, B und C sowie den Größen a, h und a/2.

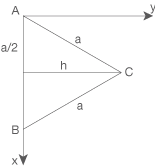Bei einem gleichseitigen Dreieck sind alle drei Seiten gleich lang. Dies bedeutet, dass die Höhe eines Punktes die gegenüberliegende Seite genau halbiert. Die Höhe $h$ von dem Punkt $C$ halbiert also die Strecke $\overline{AB}$ . Das gegebene Dreieck $ABC$ hat die Seitenlänge $a$ . Demnach hat der Punkt $C$ einen $x$ -Wert von $\frac{a}{2}$ .

Den $y$ -Wert des Punktes $B$ kannst du mit dem Satz des Pythagoras berechnen.

$\boldsymbol{c^2=a^2+b^2}$

Die Strecke $\overline{AC}$ , die Höhe $h$ und die Hälfte der Strecke $\overline{AB}$ bilden ein rechtwinkliges Dreieck. Die Länge der Höhe $h$ entspricht dabei dem $y$ -Wert des Punktes $C$ . Das $a$ und das $b$ entspricht den Katheten des Dreiecks, also $\frac{a}{2}$ und $h$ . Das $c$ ist hier die Hypotenuse. In deinem Fall besitzt diese Strecke $c$ eine Länge von $a$ LE.

Diese Werte kannst du in die Gleichung des Satz des Pythagoras einsetzen und nach der Höhe $h$ auflösen. Du erhältst demnach folgende Gleichung:

$\begin{array}{rcl} a^2&=&\left(\frac{a}{2}\right)^2+h^2\\[5pt] a^2&=&\frac{a^2}{4}+h^2&\scriptsize \mid\; -\frac{a^2}{4}\\[5pt] a^2-\frac{a^2}{4}&=&h^2\\[5pt] \frac{3a^2}{4}&=&h^2&\scriptsize \mid\; \sqrt{\;}\\[5pt] \sqrt{\frac{3a^2}{4}}&=&h\\[5pt] h&=&\frac{a}{2}\sqrt{3} \end{array}$

Der $y$ -Wert des Punktes $C$ beträgt $\frac{a}{2}\sqrt{3}$ .

Da die Grundfläche der Pyramide in der $xy$ -Ebene liegt, haben alle Punkte der Grundfläche die $z$ -Koordinate $z=0$ . Dies gilt demnach auch für den Punkt $C$ .

Der Punkt $C$ hat die Koordinaten $C\left(\frac{a}{2}\mid\;\frac{a}{2}\sqrt{3}\mid\;0\right)$ .

$\blacktriangleright$ Berechne den Schnittpunkt $\boldsymbol S$ der Seitenhalbierenden

Nun sollst du den Schnittpunkt der Seitenhalbierenden des Dreiecks $ABC$ berechnen. Die Seitenhalbierenden schneiden sich alle in einem Punkt. Daher genügt es, den Schnittpunkt von zwei Seitenhalbierenden zu berechnen. Du kannst folgendermaßen vorgehen:

Stelle eine Parametergleichung für zwei Seitenhalbierenden auf.

Setze diese Parametergleichungen gleich.

Löse das lineare Gleichungssystem.

Berechne die Koordinaten des Punktes $S$ .

Um eine Parametergleichung aufstellen zu können, benötigst du zwei Punkte. Zum einen den Eckpunkt des Dreiecks und den Mittelpunkt der gegenüberliegenden Strecke. Den Mittelpunkt einer Strecke zwischen den Punkten $P$ und $Q$ berechnest du mit folgender Formel:

$\overrightarrow{OM}=\frac{1}{2}\cdot\left(\overrightarrow{OP}+\overrightarrow{OQ}\right)$

Es gibt nun verschiedene Möglichkeiten, von welchen Seitenhalbierenden du eine Parametergleichung aufstellst und den Schnittpunkt berechnest:

Lösungsweg $\boldsymbol A$ : Schnittpunkt der Seitenhalbierenden durch die Punkte $A$ und $B$

Lösungsweg $\boldsymbol B$ : Schnittpunkt der Seitenhalbierenden durch die Punkte $A$ und $C$

Eine weitere Möglichkeit wäre, den Schnittpunkt der Seitenhalbierenden durch die Punkte $B$ und $C$ zu berechnen. Dieser Lösungsweg wird hier nicht aufgeführt.

$\blacktriangleright\blacktriangleright$ Lösungsweg A

1. Schritt: Aufstellen der Gleichungen der Seitenhalbierende durch $A$

Um eine Parametergleichung der Seitenhalbierenden durch den Punkt $A$ aufstellen zu können, brauchst du den Mittelpunkt $M_{BC}$ der Strecke $\overline{BC}$ .

$\begin{array}{rcl} \overrightarrow{OM_{BC}}&=&\frac{1}{2}\cdot\left(\overrightarrow{OB}+\overrightarrow{OC}\right)\\[5pt] &=&\frac{1}{2}\cdot\left(\begin{pmatrix}a\\0\\0\end{pmatrix}+\begin{pmatrix}\frac{a}{2}\\\frac{a}{2}\sqrt{3}\\0\end{pmatrix}\right)&=&\frac{1}{2}\cdot\begin{pmatrix}\frac{3a}{2}\\[5pt] \frac{a}{2}\sqrt{3}\\0\end{pmatrix}&=&\begin{pmatrix}\frac{3a}{4}\\[5pt] \frac{a}{4}\sqrt{3}\\0\end{pmatrix} \end{array}$

Der Mittelpunkt $M_{BC}$ hat die Koordinaten $\boldsymbol{M_{BC}\left(\frac{3a}{4}\mid\;\frac{a}{4}\sqrt{3}\mid\;0\right)}$ .

Nun kannst du eine Parametergleichung der Seitenhalbierende durch $A$ aufstellen:

$\begin{array}{rcl} g:\overrightarrow{x}&\overrightarrow{OA}+t\cdot\overrightarrow{AM_{BC}}=\begin{pmatrix}0\\0\\0\end{pmatrix}+t\cdot\left(\begin{pmatrix}\frac{3a}{4}\\ \frac{a}{4}\sqrt{3}\\0\end{pmatrix}-\begin{pmatrix}0\\0\\0\end{pmatrix}\right)=t\cdot\begin{pmatrix}\frac{3a}{4}\\ \frac{a}{4}\sqrt{3}\\0\end{pmatrix}\\ \end{array}$

2. Schritt: Aufstellen der Gleichungen der Seitenhalbierende durch $B$

Um eine Parametergleichung der Seitenhalbierenden durch den Punkt $B$ aufstellen zu können, brauchst du den Mittelpunkt $M_{AC}$ der Strecke $\overline{AC}$ .

$\begin{array}{rcl} \overrightarrow{OM_{AC}}&=&\frac{1}{2}\cdot\left(\overrightarrow{OA}+\overrightarrow{OC}\right)\\[5pt] &=&\frac{1}{2}\cdot\left(\begin{pmatrix}0\\0\\0\end{pmatrix}+\begin{pmatrix}\frac{a}{2}\\ \frac{a}{2}\sqrt{3}\\0\end{pmatrix}\right)=\frac{1}{2}\cdot\begin{pmatrix}\frac{a}{2}\\ \frac{a}{2}\sqrt{3}\\0\end{pmatrix}=\begin{pmatrix}\frac{a}{4}\\ \frac{a}{4}\sqrt{3}\\0\end{pmatrix}\\ \end{array}$

Der Mittelpunkt $M_{AC}$ hat die Koordinaten $\boldsymbol{M_{AC}\left(\frac{a}{4}\mid\;\frac{a}{4}\sqrt{3}\mid\;0\right)}$ .

Nun kannst du eine Parametergleichung der Seitenhalbierende durch den Punkt $B$ aufstellen:

$\begin{array}{rcl} h:\overrightarrow{x}&=&\overrightarrow{OB}+s\cdot\overrightarrow{BM_{AC}}=\begin{pmatrix}a\\0\\0\end{pmatrix}+s\cdot\left(\begin{pmatrix}\frac{a}{4}\\ \frac{a}{4}\sqrt{3}\\0\end{pmatrix}-\begin{pmatrix}a\\0\\0\end{pmatrix}\right)=\begin{pmatrix}a\\0\\0\end{pmatrix}+s\cdot\begin{pmatrix}\frac{-3a}{4}\\ \frac{a}{4}\sqrt{3}\\0\end{pmatrix}\\ \end{array}$

3. Schritt: Gleichsetzen der Parametergleichungen

Um den Schnittpunkt der Geraden $g$ und $h$ zu bestimmen, setzt du sie gleich.

$\begin{array}{rcl} g&=&h\\[5pt] t\cdot\begin{pmatrix}\frac{3a}{4}\\ \frac{a}{4}\sqrt{3}\\0\end{pmatrix}&=&\begin{pmatrix}a\\0\\0\end{pmatrix}+s\cdot\begin{pmatrix}\frac{-3a}{4}\\ \frac{a}{4}\sqrt{3}\\0\end{pmatrix}&\scriptsize \mid\; -s\cdot\begin{pmatrix}\frac{-3a}{4}\\ \frac{a}{4}\sqrt{3}\\0\end{pmatrix}\\[5pt] t\cdot\begin{pmatrix}\frac{3a}{4}\\ \frac{a}{4}\sqrt{3}\\0\end{pmatrix}-s\cdot\begin{pmatrix}\frac{-3a}{4}\\ \frac{a}{4}\sqrt{3}\\0\end{pmatrix}&=&\begin{pmatrix}a\\0\\0\end{pmatrix}\\ \end{array}$

Daraus erhältst du folgendes lineares Gleichungssystem:

$\begin{array}{llll} Ⅰ\quad\frac{3a}{4}\cdot t&+&\frac{3a}{4}\cdot s&=&a\\[5pt] Ⅱ\quad\frac{a}{4}\sqrt{3}\cdot t&-&\frac{a}{4}\sqrt{3}\cdot s&=&0\\[5pt] \end{array}$

4. Schritt: Lösen des Gleichungssystems

Hier wird nun zunächst die Gleichung $Ⅱ$ nach einer Variablen aufgelöst.

$\begin{array}{lll} \frac{a}{4}\sqrt{3}\cdot t-\frac{a}{4}\sqrt{3}\cdot s&=&0&\scriptsize \mid\; +\frac{a}{4}\sqrt{3}\cdot s\\[2pt] \frac{a}{4}\sqrt{3}\cdot t&=&\frac{a}{4}\sqrt{3}\cdot s&\scriptsize \mid\; \cdot \frac{4}{a\sqrt{3}}\\[2pt] t&=&s\\ \end{array}$

Du kannst nun in Gleichung Ⅰ das $s$ durch $t$ ersetzen:

$\begin{array}{rll} \frac{3a}{4}\cdot t+\frac{3a}{4}\cdot s&=&a\\[2pt] \frac{3a}{4}\cdot t+\frac{3a}{4}\cdot t&=&a\\[2pt] \frac{6a}{4}\cdot t&=&a&\scriptsize \mid\; \cdot\frac{4}{6a}\\[2pt] t&=&a\cdot\frac{4}{6a}\\[2pt] t&=&\frac{2}{3} \end{array}$

Du erhältst also als Lösung des Gleichungssystems $s=t=\frac{2}{3}$ .

5. Schritt: Berechne die Koordinaten des Punktes $\boldsymbol S$

Um nun die Koordinaten des Schnittpunktes $S$ der Seitenhalbierenden zu berechnen, setzt du das $t$ oder $s$ in die jeweilige Parametergleichung ein.

$\begin{array} \overrightarrow{OS}&=&t\cdot\begin{pmatrix}\frac{3a}{4}\\ \frac{a}{4}\sqrt{3}\\0\end{pmatrix}=\frac{2}{3}\cdot\begin{pmatrix}\frac{3a}{4}\\ \frac{a}{4}\sqrt{3}\\0\end{pmatrix}=\overrightarrow{OS}&\begin{pmatrix}\frac{a}{2}\\ \frac{a}{6}\sqrt{3}\\0\end{pmatrix}\\ \end{array}$

Der Schnittpunkt $S$ der Seitenhalbierenden hat die Koordinaten $\boldsymbol{S\left(\frac{a}{2}\mid\;\frac{a}{6}\sqrt{3}\mid\;0\right)}$ .

$\blacktriangleright\blacktriangleright$ Lösungsweg B

1. Schritt: Aufstellen der Gleichungen der Seitenhalbierende durch $A$

Wie du eine Parametergleichung der Seitenhalbierende durch den Punkt $A$ aufstellst, siehst du bei dem Lösungsweg $A$ . Eine mögliche Gleichung lautet:

$\begin{array}{rcl} g:\overrightarrow{x}&=&t\cdot\begin{pmatrix}\frac{3a}{4}\\ \frac{a}{4}\sqrt{3}\\0\end{pmatrix}\\ \end{array}$

Nun benötigst du noch eine Parametergleichung durch den Punkt $C$ .

2. Schritt: Aufstellen der Gleichungen der Seitenhalbierende durch $C$

Um eine Parametergleichung der Seitenhalbierenden durch den Punkt $C$ aufstellen zu können, benötigst du den Mittelpunkt $M_{AB}$ der Strecke $\overline{AB}$ .

$\begin{array}{rcl} \overrightarrow{OM_{AB}}&=&\frac{1}{2}\cdot\left(\overrightarrow{OA}+\overrightarrow{OB}\right)\\[5pt] &=&\frac{1}{2}\cdot\left(\begin{pmatrix}0\\0\\0\end{pmatrix}+\begin{pmatrix}a\\0\\0\end{pmatrix}\right)=\frac{1}{2}\cdot\begin{pmatrix}a\\0\\0\end{pmatrix}=\begin{pmatrix}\frac{a}{2}\\0\\0\end{pmatrix}\\ \end{array}$

Der Mittelpunkt $M_{AB}$ hat die Koordinaten $\boldsymbol{M_{AB}\left(\frac{a}{2}\mid\;0\mid\;0\right)}$ .

Nun kannst du eine Parametergleichung der Seitenhalbierende durch den Punkt $C$ aufstellen:

$\begin{array}{rcl} i:\overrightarrow{x}&\overrightarrow{OC}+r\cdot\overrightarrow{CM_{AB}}=\begin{pmatrix}\frac{a}{2}\\ \frac{a}{2}\sqrt{3}\\0\end{pmatrix}+r\cdot\left(\begin{pmatrix}\frac{a}{2}\\ 0\\0\end{pmatrix}-\begin{pmatrix}\frac{a}{2}\\ \frac{a}{2}\sqrt{3}\\0\end{pmatrix}\right)=\begin{pmatrix}\frac{a}{2}\\ \frac{a}{2}\sqrt{3}\\0\end{pmatrix}+r\cdot\begin{pmatrix}0\\ -\frac{a}{2}\sqrt{3}\\0\end{pmatrix}\\ \end{array}$

3. Schritt: Gleichsetzen der Parametergleichungen

Um den Schnittpunkt der Geraden $g$ und $i$ zu bestimmen, setzt du sie gleich.

$\begin{array}{rcl} g&=&i\\[5pt] t\cdot\begin{pmatrix}\frac{3a}{4}\\ \frac{a}{4}\sqrt{3}\\0\end{pmatrix}&=&\begin{pmatrix}\frac{a}{2}\\ \frac{a}{2}\sqrt{3}\\0\end{pmatrix}+r\cdot\begin{pmatrix}0\\ -\frac{a}{2}\sqrt{3}\\0\end{pmatrix}&\scriptsize\quad\mid\; -r\cdot\begin{pmatrix}0\\ -\frac{a}{2}\sqrt{3}\\0\end{pmatrix}\\ t\cdot\begin{pmatrix}\frac{3a}{4}\\ \frac{a}{4}\sqrt{3}\\0\end{pmatrix}-r\cdot\begin{pmatrix}0\\ -\frac{a}{2}\sqrt{3}\\0\end{pmatrix}&=&\begin{pmatrix}\frac{a}{2}\\ \frac{a}{2}\sqrt{3}\\0\end{pmatrix}\\ \end{array}$

Daraus erhältst du folgendes lineares Gleichungssystem:

$\begin{array}{rcl} Ⅰ&=&\frac{3a}{4}\cdot t&-&0\cdot r&=&\frac{a}{2}\\ Ⅱ&=&\frac{a}{4}\sqrt{3}\cdot t&+&\frac{a}{2}\sqrt{3}\cdot r&=&\frac{a}{2}\sqrt{3} \end{array}$

4. Schritt: Lösen des Gleichungssystems Wenn du dir die Gleichung $Ⅰ$ genau anschaust, erkennst du, dass nur die Variable $t$ in der Gleichung vorkommt. Diese Gleichung kannst du also direkt lösen:

$\begin{array} \frac{3a}{4}\cdot t&\frac{a}{2}&\scriptsize \mid\; \cdot\frac{4}{3a}\\[2pt] t&\frac{a}{2}\cdot\frac{4}{3a}\\[2pt] t&\frac{2}{3}\\ \end{array}$

Das $t$ hat einen Wert von $\boldsymbol{t=\frac{2}{3}}$ . Diesen kannst du nun in die Gleichung Ⅰ einsetzen.

$\begin{array} \frac{a}{4}\sqrt{3}\cdot t+\frac{a}{2}\sqrt{3}\cdot r&=&\frac{a}{2}\sqrt{3}\\[5pt] \frac{a}{4}\sqrt{3}\cdot \frac{2}{3}+\frac{a}{2}\sqrt{3}\cdot r&=&\frac{a}{2}\sqrt{3}\\[5pt] \frac{a}{6}\sqrt{3}+\frac{a}{2}\sqrt{3}\cdot r&=&\frac{a}{2}\sqrt{3}&\scriptsize \mid\; -\frac{a}{6}\sqrt{3}\\ \frac{a}{2}\sqrt{3}\cdot r&=&\frac{a}{2}\sqrt{3}-\frac{a}{6}\sqrt{3}\\[5pt] \frac{a}{2}\sqrt{3}\cdot r&=&\frac{3a}{6}\sqrt{3}-\frac{a}{6}\sqrt{3}\\[5pt] \frac{a}{2}\sqrt{3}\cdot r&=&\frac{a}{3}\sqrt{3}&\scriptsize \mid\; \cdot\frac{2}{a\sqrt{3}}\\[5pt] r&=&\frac{a}{3}\sqrt{3}\cdot\frac{2}{a\sqrt{3}}\\[5pt] r&=&\frac{2}{3} \end{array}$

Das $r$ hat ebenfalls einen Wert von $\boldsymbol{r=\frac{2}{3}}$ .

5. Schritt: Berechne die Koordinaten des Punktes $\boldsymbol S$

Um nun die Koordinaten des Schnittpunktes $S$ der Seitenhalbierenden zu berechnen, setzt du das $t$ oder $r$ in die jeweilige Parametergleichung ein. Hier wird das $t=\frac{2}{3}$ in die Parametergleichung $g$ eingesetzt:

$\begin{array} \overrightarrow{OS}&=&t\cdot\begin{pmatrix}\frac{3a}{4}\\ \frac{a}{4}\sqrt{3}\\0\end{pmatrix}=\frac{2}{3}\cdot\begin{pmatrix}\frac{3a}{4}\\ \frac{a}{4}\sqrt{3}\\0\end{pmatrix}=\begin{pmatrix}\frac{a}{2}\\ \frac{a}{6}\sqrt{3}\\0\end{pmatrix}\\ \end{array}$

Der Schnittpunkt $S$ der Seitenhalbierenden hat die Koordinaten $\boldsymbol{S\left(\frac{a}{2}\mid\;\frac{a}{6}\sqrt{3}\mid\;0\right)}$ .

$\blacktriangleright$ Berechne die Koordinaten des Punktes $\boldsymbol D$

Der Punkt $D$ entspricht der Spitze der Pyramide. Überlege dir zunächst, in welchem besonderen Punkt die Höhe der Pyramide auf die Grundfläche trifft. Beachte dabei die drei kongruenten rechtwinklig-gleichschenkligen Dreiecke. Es ist außerdem wichtig in welchem Winkel die Seitenkanten an der Spitze der Pyramide aufeinander treffen.

Dadurch, dass die drei Seitenflächen der Pyramide gleichschenklig und kongruent sind, bedeutet das, dass die Höhe der Pyramide in der Mitte der Grundfläche auftrifft. Dieser Punkt entspricht dem Schnittpunkt $S\left(\frac{a}{2}\mid\;\frac{a}{6}\sqrt{3}\mid\;0\right)$ der Seitenhalbierenden. Der Punkt $D$ hat demnach die Koordinaten $\boldsymbol{D\left(\frac{a}{2}\mid\;\frac{a}{6}\sqrt{3}\mid\; z>0\right)}$ .

Nun musst du nur noch die $z$ -Koordinate des Punktes $D$ berechnen.

Du weißt, dass die Kanten an der Spitze $D$ einen rechten Winkel haben. Das heißt, dass das Skalarprodukt zweier Kanten Null ergeben muss. Es gilt also:

$\overrightarrow{AD}\circ\overrightarrow{BD}=0$ (Lösungsweg $A$ )

$\overrightarrow{AD}\circ\overrightarrow{CD}=0$ (Lösungsweg $B$ )

$\overrightarrow{BD}\circ\overrightarrow{CD}=0$

Hier werden nun zwei verschiedene Lösungswege aufgezeigt.

$\blacktriangleright\blacktriangleright$ Lösungsweg A Bei diesem Lösungsweg gilt:

$\overrightarrow{AD}\circ\overrightarrow{BD}=0$

Berechne die einzelnen Richtungsvektoren und löse nach $z$ auf.

$\begin{array}{rcl} \overrightarrow{AD}\circ\overrightarrow{BD}&=&0\\[5pt] \left(\begin{pmatrix}\frac{a}{2}\\ \frac{a}{6}\sqrt{3}\\z\end{pmatrix}-\begin{pmatrix}0\\0\\0\end{pmatrix}\right)\circ\left(\begin{pmatrix}\frac{a}{2}\\ \frac{a}{6}\sqrt{3}\\z\end{pmatrix}-\begin{pmatrix}a\\0\\0\end{pmatrix}\right)&=&0\\[5pt] \begin{pmatrix}\frac{a}{2}\\ \frac{a}{6}\sqrt{3}\\z\end{pmatrix}\circ\begin{pmatrix}-\frac{a}{2}\\ \frac{a}{6}\sqrt{3}\\z\end{pmatrix}&=&0\\[5pt] -\frac{a^2}{2^2}+\frac{a^2}{6^2}\cdot\sqrt{3}^2+z^2&=&0\\[5pt] -\frac{a^2}{4}+\frac{a^2}{36}\cdot3+z^2&=&0\\[5pt] -\frac{a^2}{4}+\frac{a^2}{12}+z^2&=&0\\[5pt] -\frac{3a^2}{12}+\frac{a^2}{12}+z^2&=&0\\[5pt] -\frac{2a^2}{12}+z^2&=&0\\[5pt] -\frac{a^2}{6}+z^2&=&0&\scriptsize \mid\; +\frac{a^2}{6}\\[5pt] z^2&=&\frac{a^2}{6}&\scriptsize \mid\; \sqrt{}\\[5pt] z&=&\sqrt{\frac{a^2}{6}}\\[5pt] z&=&\frac{a}{6}\sqrt{6} \end{array}$

Der Punkt $D$ hat die Koordinaten $\boldsymbol{D\left(\frac{a}{2}\mid\;\frac{a}{6}\sqrt{3}\mid\;\frac{a}{6}\sqrt{6}\right)}$ .

$\blacktriangleright\blacktriangleright$ Lösungsweg B

Bei diesem Lösungsweg gilt:

$\overrightarrow{AD}\circ\overrightarrow{CD}=0$

Berechne die einzelnen Richtungsvektoren und löse nach $z$ auf.

$\begin{array}{rcl} \overrightarrow{AD}\circ\overrightarrow{CD}&=&0&\\[5pt] \left(\begin{pmatrix}\frac{a}{2}\\ \frac{a}{6}\sqrt{3}\\z\end{pmatrix}-\begin{pmatrix}0\\0\\0\end{pmatrix}\right)\circ\left(\begin{pmatrix}\frac{a}{2}\\ \frac{a}{6}\sqrt{3}\\z\end{pmatrix}-\begin{pmatrix}\frac{a}{2}\\ \frac{a}{2}\sqrt{3}\\0\end{pmatrix}\right)&=&0\\[5pt] \begin{pmatrix}\frac{a}{2}\\ \frac{a}{6}\sqrt{3}\\z\end{pmatrix}\circ\begin{pmatrix}0\\-\frac{a}{3}\sqrt{3}\\z\end{pmatrix}&=&0\\[5pt] 0-\frac{a^2}{3\cdot6}\sqrt{3}^2+z^2&=&0&\scriptsize \mid\; +\frac{a^2}{3\cdot6}\sqrt{3}\\[5pt] 0-\frac{a^2}{6}+z^2&=&0&\scriptsize \mid\; +\frac{a^2}{6}\\[5pt] z^2&=&\frac{a^2}{6}&\scriptsize \mid\; \sqrt{}\\[5pt] z&=&\sqrt{\frac{a^2}{6}}&\\[5pt] z&=&\frac{a}{\sqrt{6}}\\[5pt] z&=&\frac{a}{6}\sqrt{6} \end{array}$

Der Punkt $D$ hat die Koordinaten $\boldsymbol{D\left(\frac{a}{2}\mid\;\frac{a}{6}\sqrt{3}\mid\;\frac{a}{6}\sqrt{6}\right)}$ .

$\blacktriangleright$ Zeige, dass der Winkel $\boldsymbol \phi$ unabhängig von $\boldsymbol a$ ist

Bei dieser Teilaufgabe sollst du zeigen, dass die Größe des Winkel $\phi$ zwischen der Seitenkante $\overline{BD}$ und der Grundfläche unabhängig von $a$ ist.

Einen Winkel zwischen einer Geraden und einer Ebene berechnest du mit folgender Formel:

$\boldsymbol{\sin\phi=\frac{\left|\overrightarrow{v}\cdot\overrightarrow{n}\right|}{\left|\overrightarrow{v}\right|\cdot\left|\overrightarrow{n}\right|}}$

Dabei entspricht der Vektor $\overrightarrow{v}$ dem Richtungsvektor einer Geraden und der Vektor $\overrightarrow{n}$ dem Normalenvektor einer Ebene. Du kannst wie folgt vorgehen:

Berechne den Richtungsvektor $\overrightarrow{BD}$ .

Überlege dir, welchen Normalenvektor $\overrightarrow{n}$ die Ebene hat, in welcher $ABC$ liegt.

Berechne den Winkel $\phi$ .

1. Schritt: Berechne den Richtungsvektor $\boldsymbol{\overrightarrow{BD}}$

Die Koordinaten der Punkte $B$ und $D$ hast du gegeben bzw. in der Teilaufgabe a) berechnet. Der Punkt $B$ hat die Koordinaten $B(a\mid\;0\mid\;0)$ und der Punkt $C$ die Koordinaten $D\left(\frac{a}{2}\mid\;\frac{a}{6}\sqrt{3}\mid\;\frac{a}{6}\sqrt{6}\right)$ . Berechne damit den Richtungsvektor $\overrightarrow{BD}$ .

$\begin{array}{rcl} \overrightarrow{BD}&=&\overrightarrow{OD}-\overrightarrow{OB}\begin{pmatrix}\frac{a}{2}\\ \frac{a}{6}\sqrt{3}\\ \frac{a}{6}\sqrt{6}\end{pmatrix}-\begin{pmatrix}a\\0\\0\end{pmatrix}\begin{pmatrix}-\frac{a}{2}\\ \frac{a}{6}\sqrt{3}\\ \frac{a}{6}\sqrt{6}\end{pmatrix}\\ \end{array}$

2. Schritt: Normalenvektor $\boldsymbol{\overrightarrow{n}}$

Die Grundfläche der Pyramide liegt in der $\boldsymbol{xy}$ -Ebene. Der Normalenvektor $\overrightarrow{n}$ steht senkrecht auf dieser Ebene. Er lautet demnach:

$\overrightarrow{n}\begin{pmatrix}0\\0\\1\end{pmatrix}$

3. Schritt: Berechne den Winkel $\boldsymbol\phi$

Du hast nun sowohl den Richtungsvektor $\overrightarrow{BD}$ , als auch den Normalenvektor $\overrightarrow{n}$ gegeben. Diese kannst du in die Formel zur Berechnung des Winkels einsetzen.

$\begin{array}{rll} \sin\phi&=\dfrac{\left|\overrightarrow{BD}\cdot\overrightarrow{n}\right|}{\left|\overrightarrow{BD}\right|\cdot\left|\overrightarrow{n}\right|}=\dfrac{\left|\begin{pmatrix}-\frac{a}{2}\\ \frac{a}{6}\sqrt{3}\\ \frac{a}{6}\sqrt{6}\end{pmatrix}\cdot\begin{pmatrix}0\\0\\1\end{pmatrix}\right|}{\left|\begin{pmatrix}-\frac{a}{2}\\ \frac{a}{6}\sqrt{3}\\ \frac{a}{6}\sqrt{6}\end{pmatrix}\right|\cdot\left|\begin{pmatrix}0\\0\\1\end{pmatrix}\right|}\\[5pt] &=\dfrac{\frac{a}{6}\sqrt{6}}{\sqrt{\left(-\dfrac{a}{2}\right)^2+\left(\dfrac{a}{6}\sqrt{3}\right)^2+\left(\dfrac{a}{6}\sqrt{6}\right)^2}\cdot\sqrt{0^2+0^2+1^2}}\\[5pt] &=\dfrac{\frac{a}{6}\sqrt{6}}{\sqrt{\dfrac{a^2}{4}+\dfrac{a^2}{36}\cdot3+\dfrac{a^2}{6^2}\cdot6}\cdot\sqrt{1}}\\[5pt] &=\dfrac{\frac{a}{6}\sqrt{6}}{\sqrt{\dfrac{a^2}{4}+\dfrac{a^2}{12}+\dfrac{a^2}{6}}\cdot1}\\[5pt] &=\dfrac{\frac{a}{6}\sqrt{6}}{\sqrt{\dfrac{3a^2}{12}+\dfrac{a^2}{12}+\dfrac{2a^2}{12}}} \\[5pt] &=\dfrac{\frac{a}{6}\sqrt{6}}{\sqrt{\frac{6a^2}{12}}}\\[5pt] &=\dfrac{\frac{a}{6}\sqrt{6}}{\sqrt{\frac{a^2}{2}}}=\dfrac{\frac{a}{6}\sqrt{6}}{\frac{a}{2}\sqrt{2}}=\dfrac{a}{6}\cdot\dfrac{2}{a}\cdot\sqrt{\dfrac{6}{2}}\\[5pt] &\dfrac{1}{3}\sqrt{3}&\scriptsize \mid\; sin^{-1}(...)\\[5pt] \phi&=sin^{-1}\left(\frac{1}{3}\sqrt{3}\right)\approx 35,26^\circ&&\\ \end{array}$

Die Größe des Winkels, den die Seitenkante $\overline{BD}$ und die Grundfläche der Pyramide einschließt, ist unabhängig von $a$ .