Pflichtaufgaben

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f: x \mapsto 5 x \cdot \mathrm{e}^{-x}.$

Der Graph von $f$ wird mit $G$ bezeichnet.

Gib die Koordinaten des Schnittpunkts von $G$ mit der $y$ -Achse an.

(1 BE)

$G$ besitzt genau einen Extrempunkt. Bestimme das Monotonieverhalten von $f.$

(4 BE)

Die Abbildung zeigt den Graphen der in $\mathbb{R}$ definierten Funktion $f$ mit $f(x)=3 \cdot \cos (x).$

Graph einer Sinusfunktion mit Achsenbeschriftungen für x und y.

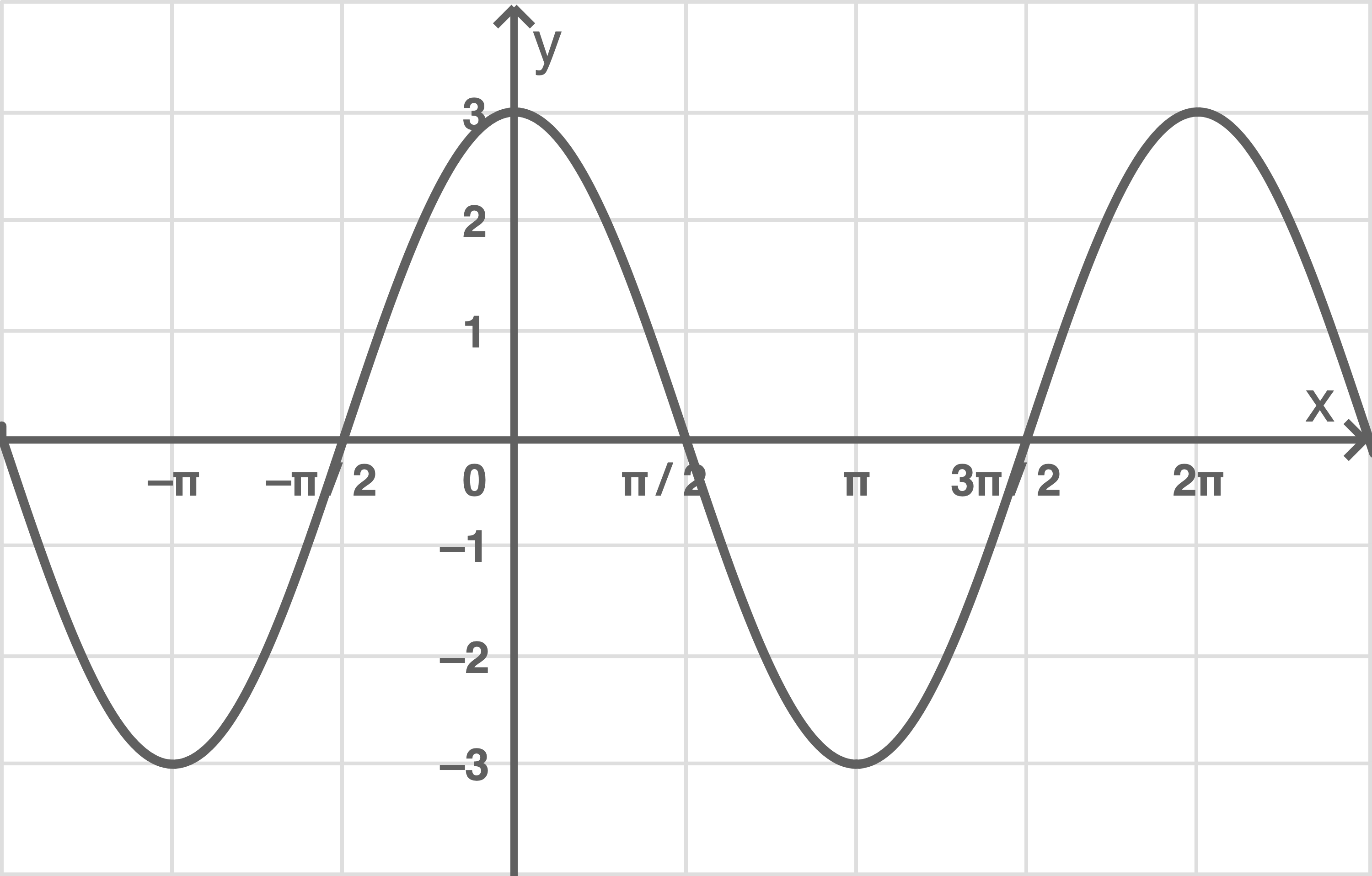
Gib den Wert des Integrals $\displaystyle\int_0^\pi f(x) \;\text{d} x$ an.

(1 BE)

Die in $\mathbb{R}$ definierte Funktion $g$ ist gegeben durch $g(x)=a \cdot f(x)+b \cdot x$ mit reellen Zahlen $a$ und $b.$ Die Punkte $(0 \mid -3)$ und $\left(\frac{\pi}{2} \mid \frac{3}{4} \pi\right)$ liegen auf dem Graphen von $g.$

Ermittle $a$ und $b.$

(4 BE)

Gegeben sind die Gerade $g: \overrightarrow{x}=\pmatrix{3\\2\\3}+t \cdot \pmatrix{1\\1\\0}$ mit $t \in \mathbb{R}$ und der Punkt $P(0\mid 4\mid 0).$

Begründe, dass $P$ nicht auf $g$ liegt.

(1 BE)

Die Gerade $h$ enthält den Punkt $P$ und schneidet die $z$ -Achse im Punkt $Q.$

Bestimme die Koordinaten von $Q$ so, dass sich die Geraden $g$ und $h$ schneiden.

(4 BE)

Die Abbildung zeigt den Graphen der Dichtefunktion einer normalverteilten Zufallsgröße $X$ mit dem Erwartungswert $\mu=50$ und der Standardabweichung $\sigma.$

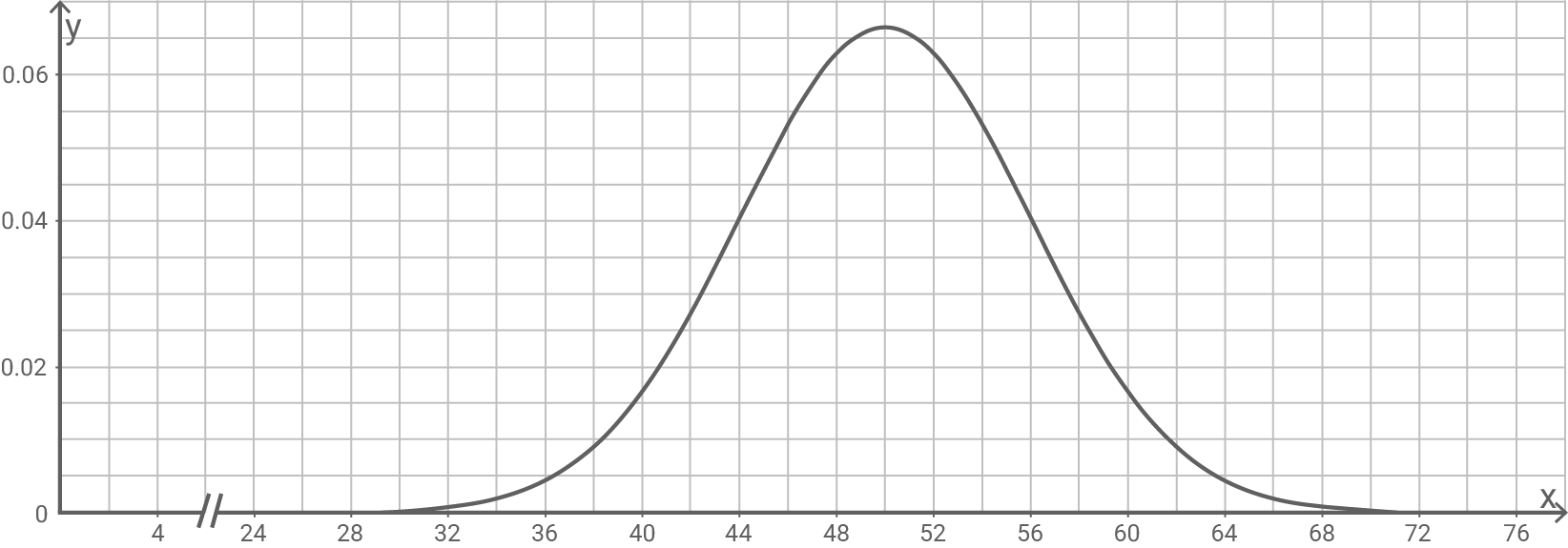
Graph mit einer Kurve, die eine Verteilung darstellt, mit Achsenbeschriftungen für x und y.

Bestimme $P(48 \leq X \leq 52).$

(2 BE)

Für eine weitere normalverteilte Zufallsgröße $Y$ mit dem gleichen Erwartungswert wie $X,$ aber einer anderen Standardabweichung, gilt $P(Y \geq 45)=0,7.$

Bestimme $P(45 \leq Y \leq 55).$

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$f(0)=5\cdot0\cdot\mathrm e^{-0}=0$

Somit folgt $(0\mid0)$ für die gesuchten Koordinaten.

Für die Ableitung von $f$ folgt mit der Produktregel:

$\(\begin{array}[t]{rlll} f$

Nullsetzen liefert:

$\(\begin{array}[t]{rlll} f$

Mit dem Satz des Nullprodukts folgt $5-5x=0,$ d.h. $x=1.$ Da nach Teilaufgabe a) auch $f(0)=0$ gilt, folgt, dass $x=1$ eine Hochstelle ist. Somit ist $f$ für $x\lt1$ streng monoton steigend und für $x\gt1$ streng monoton fallend.

Die Abbildung zeigt, dass der Graph von $f$ zwischen $0$ und $\pi$ gleichgroße Flächen unterhalb sowie oberhalb der $x$ -Achse mit dieser einschließt. Somit gilt:

$\displaystyle\int_{0}^{\pi}f(x)\;\mathrm dx=0$

$\begin{array}[t]{rlll} g(0)&=&-3 \\[5pt] a\cdot f(0)+b\cdot0&=&-3 \\[5pt] 3a&=&-3 &\mid\;:3 \\[5pt] a&=&-1 \end{array}$

$\begin{array}[t]{rlll} g\left(\dfrac{\pi}{2}\right)&=&\dfrac{3}{4}\pi \\[5pt] -f\left(\dfrac{\pi}{2}\right)+b\cdot\dfrac{\pi}{2}&=&\dfrac{3}{4}\pi \\[5pt] \dfrac{\pi}{2}b&=&\dfrac{3}{4}\pi &\mid\;\cdot\frac{2}{\pi} \\[5pt] b&=&\dfrac{3}{2} \end{array}$

Alle Punkte der Geraden besitzen die $z$ -Koordinate $3.$ Da das nicht der $z$ -Koordinate von $P$ entspricht, kann $P$ nicht auf $g$ liegen.

Gleichsetzen einer allgemeinen Geradengleichung von $h,$ welche in diesem Fall für $s=1$ die $z$ -Achse schneidet, mit der Geradengleichung von $g$ liefert:

$\pmatrix{3\\2\\3}+t\cdot\pmatrix{1\\1\\0}=\pmatrix{0\\4\\0}+s\cdot\pmatrix{0\\-4\\z}$

Daraus ergibt sich folgendes lineares Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&3+t&=& 0 \\ \text{II}\quad&2+t&=&4-4s & \\ \text{III}\quad&3&=&zs & \\ \end{array}$

Gleichung $\text{I}$ liefert direkt $t=-3.$ Einsetzen in Gleichung $\text{II}$ ergibt:

$\begin{array}[t]{rlll} 2-3&=&4-4s &\mid\;-4 \\[5pt] -5&=&-4s &\mid\;:(-4) \\[5pt] \dfrac{5}{4}&=&s \end{array}$

Durch Einsetzen in Gleichung $\text{III}$ folgt dann für $z:$

$\begin{array}[t]{rlll} 3&=&\dfrac{5}{4}z &\mid\;\cdot\frac{4}{5} \\[5pt] \dfrac{12}{5}&=&z \end{array}$

Mit $s=1$ folgt somit für die gesuchten Koordinaten $Q\left(0\mid0\mid\frac{12}{5}\right).$

Die gesuchte Wahrscheinlichkeit lässt sich mit Hilfe der Abbildung ungefähr als der Flächeninhalt eines Balkens der Breite $4$ und Höhe $0,065$ ablesen, somit folgt:

$\begin{array}[t]{rlll} P(48 \leq X \leq 52)&=&4\cdot0,065 \\[5pt] &=&0,26 \\[5pt] &=&26\,\% \end{array}$

Da die Dichtefunktion von $Y$ ebenfalls symmetrisch zu $x=50$ ist, folgt aus $P(Y\geq45)=0,7$ direkt $P(Y\leq45)=0,3$ und $P(Y\geq55)=0,3$ und somit ergibt sich:

Rechenweg anzeigen

$P(45 \leq Y \leq 55) = 0,4$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?