Pflichtaufgabe 1 – Ohne Hilfsmittel
1.
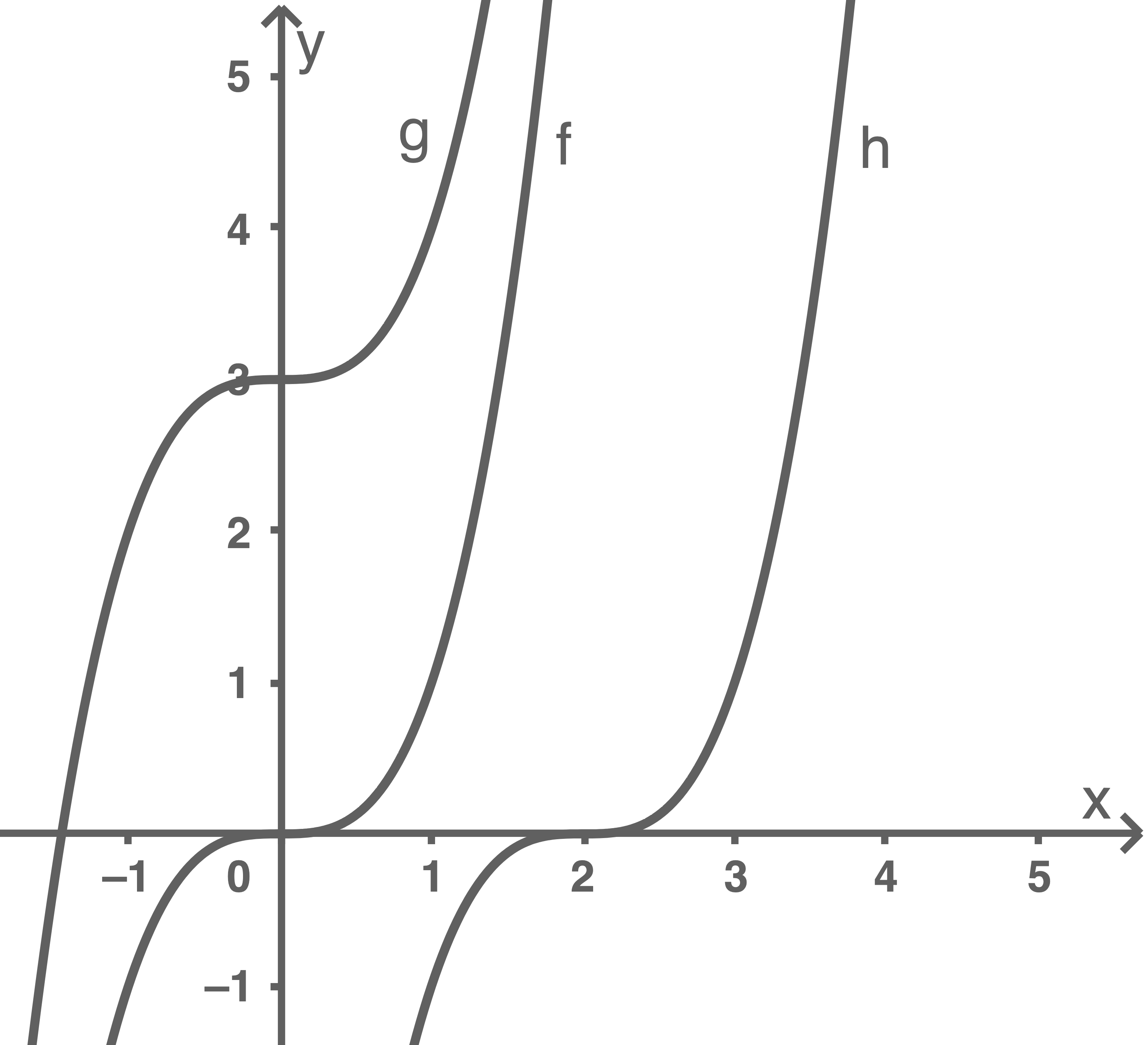
Dargestellt sind die Graphen der Funktionen 
 und
und  Die Funktion
Die Funktion  ist gegeben durch
ist gegeben durch 
 Die Graphen von
Die Graphen von  und
und  gehen aus dem Graphen von
gehen aus dem Graphen von  durch Verschiebung hervor.
durch Verschiebung hervor.
Gib je eine mögliche Gleichung von und
und  an.
an.
Gib je eine mögliche Gleichung von
(2 BE)
2.
Gegeben ist die Funktion  durch
durch 

a)
Skizziere den Graphen der Funktion 
(1 BE)
b)
Für jede reelle Zahl  ist eine Gerade
ist eine Gerade  durch
durch  gegeben.
gegeben.
Gib alle Werte für so an, dass die Gerade
so an, dass die Gerade  und der Graph von
und der Graph von  im Intervall
im Intervall  genau zwei Punkte gemeinsam haben.
genau zwei Punkte gemeinsam haben.
Gib alle Werte für
(2 BE)
3.
Im Unterricht der Klasse 10 soll der Term 
 vereinfacht werden. Fünf Schülerlösungen werden vorgestellt.
vereinfacht werden. Fünf Schülerlösungen werden vorgestellt.




 Gib alle richtigen Vereinfachungen an.
Gib alle richtigen Vereinfachungen an.
(2 BE)
4.
Tina hat ein Zufallsexperiment durchgeführt. Sie bestimmt die Wahrscheinlichkeit des Ereignisses  mit einem Baumdiagramm und rechnet:
mit einem Baumdiagramm und rechnet:  Beschreibe ein zugehöriges Zufallsexperiment.
Beschreibe ein zugehöriges Zufallsexperiment.
(1 BE)
5.
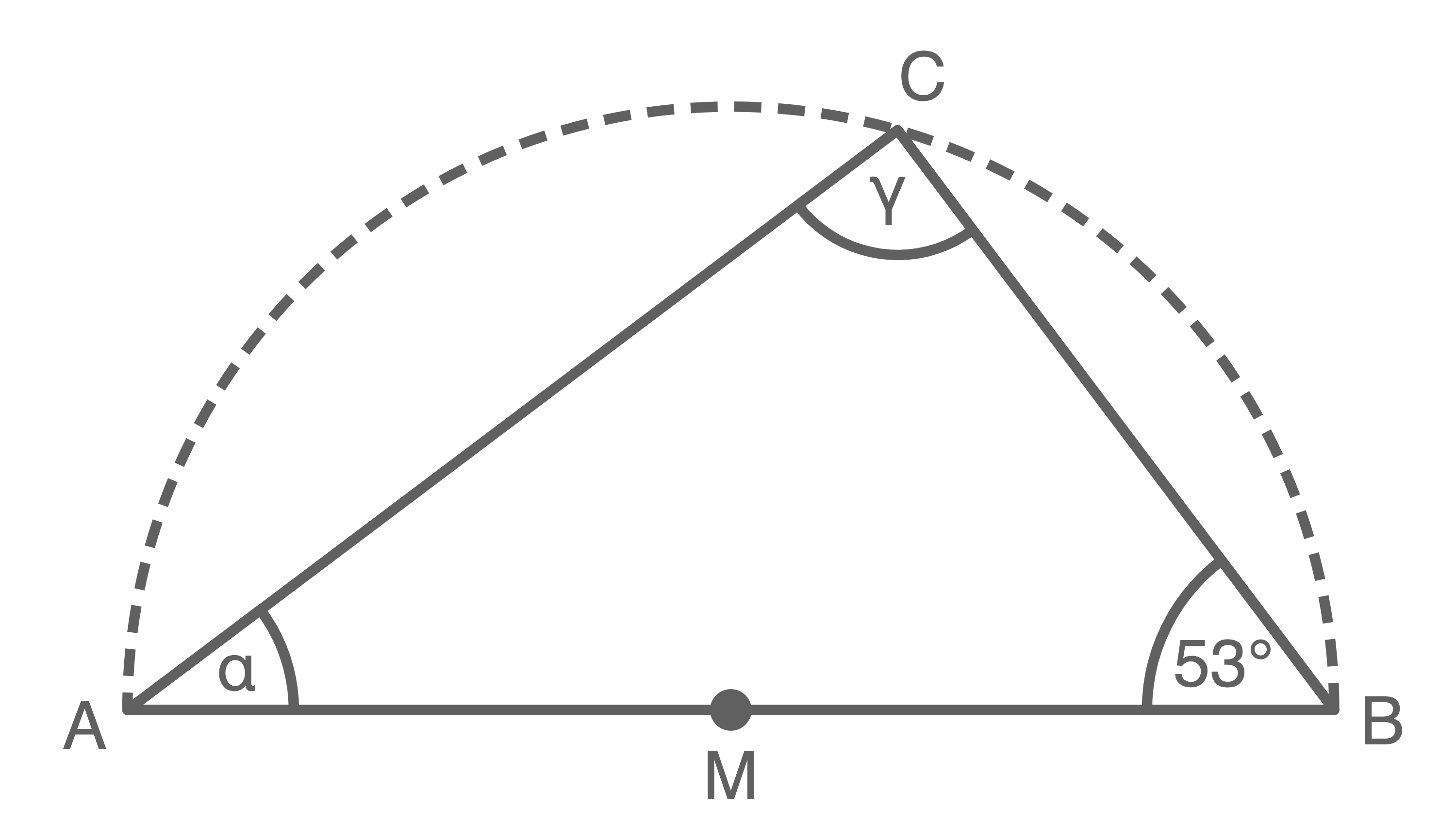
Begründe, dass der Winkel  eine Größe von
eine Größe von  hat.
hat.

(2 BE)
1.
Der Graph der Funktion  ist im Vergleich zum Graphen der Funktion
ist im Vergleich zum Graphen der Funktion  um drei Einheiten nach oben verschoben.
um drei Einheiten nach oben verschoben.
 Der Graph der Funktion
Der Graph der Funktion  ist im Vergleich zum Graphen der Funktion
ist im Vergleich zum Graphen der Funktion  um zwei Einheiten nach rechts verschoben.
um zwei Einheiten nach rechts verschoben.

2.
a)
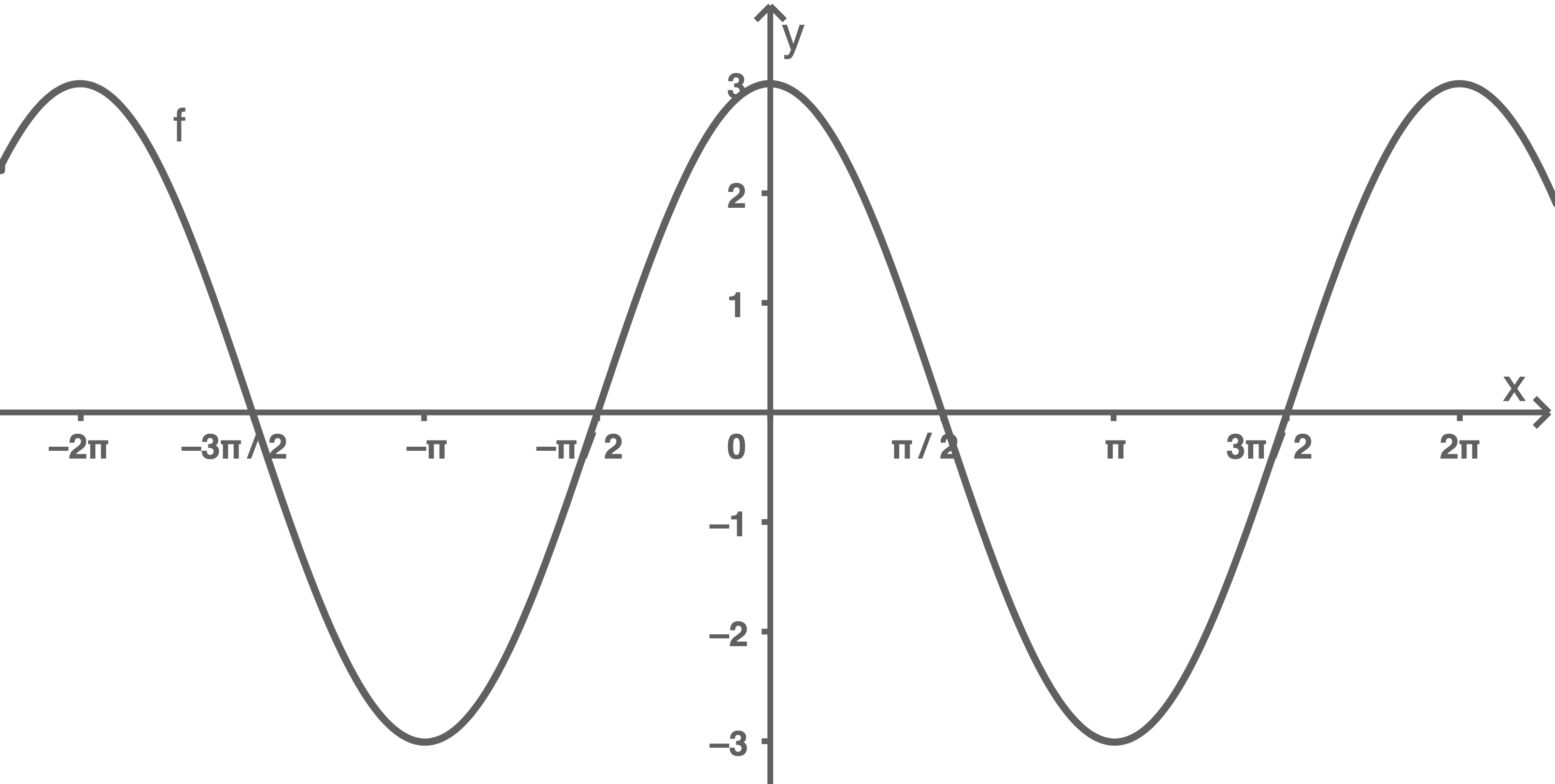
b)
In der Skizze aus Teilaufgabe a) lässt sich erkennen, dass die Gerade  und der Graph von
und der Graph von  im angegebenen Intervall für alle Werte von
im angegebenen Intervall für alle Werte von  mit
mit  genau zwei gemeinsame Schnittpunkte haben.
Außerdem hat die Gerade
genau zwei gemeinsame Schnittpunkte haben.
Außerdem hat die Gerade  im angegebenen Intervall für den Wert
im angegebenen Intervall für den Wert  genau zwei gemeinsame Schnittpunkte mit dem Graphen von
genau zwei gemeinsame Schnittpunkte mit dem Graphen von 
3.
Mit den Potenzgesetzen kann der Term wie folgt vereinfacht werden:
 Die Schülerlösungen
Die Schülerlösungen  und
und  sind richtig.
sind richtig.
4.
Ein mögliches Zufallsexperiment ist das folgende:
Tina zieht aus einer Urne mit 3 grünen und einer blauen Kugel zweimal ohne Zurücklegen. Das Ereignis  tritt ein, wenn Tina zweimal hintereinander eine grüne Kugel zieht.
tritt ein, wenn Tina zweimal hintereinander eine grüne Kugel zieht.
5.
Nach dem Satz des Thales gilt  Da in einem Dreieck die Innenwinkelsumme
Da in einem Dreieck die Innenwinkelsumme  betragen muss, gilt:
betragen muss, gilt:
