Wahlaufgabe 1
1.
Ein Waldstück soll neu aufgeforstet werden. Dieses Waldstück kann näherungsweise durch das Viereck  dargestellt werden.
dargestellt werden.
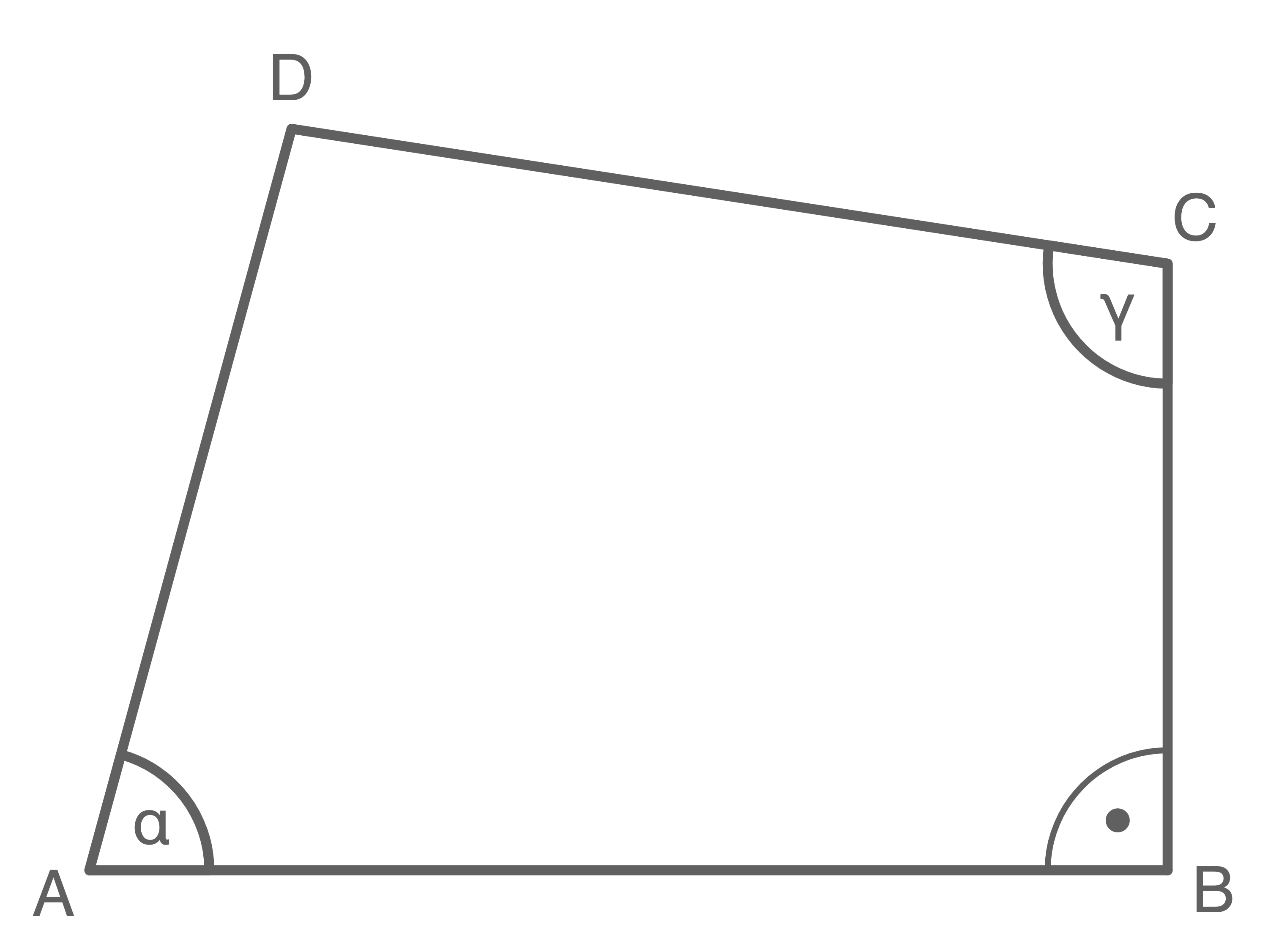



 Der Teil des Waldes, der durch die Dreiecksfläche
Der Teil des Waldes, der durch die Dreiecksfläche  dargestellt wird, soll mit Buchen, der Rest mit Fichten bepflanzt werden.
dargestellt wird, soll mit Buchen, der Rest mit Fichten bepflanzt werden.

Skizze nicht maßstäblich
a)
Berechne die Größe der Fläche, die mit Buchen bepflanzt werden soll.
Weise nach, dass die mit Fichten zu bepflanzende Fläche etwa groß ist.
groß ist.
Weise nach, dass die mit Fichten zu bepflanzende Fläche etwa
(5 BE)
b)
In Deutschland ist knapp ein Drittel der Fläche mit Wald bedeckt. Der Anteil der mit Nadelbäumen bedeckten Fläche beträgt 59 %, der mit Laubbäumen 41 %.
Untersuche, ob auch auf dem neu aufzuforstenden Waldstück etwa diese Anteile vorliegen.
Untersuche, ob auch auf dem neu aufzuforstenden Waldstück etwa diese Anteile vorliegen.
(2 BE)
c)
Der Holzbestand von Wäldern wird in Festmetern angegeben. Bei natürlichem, ungestörtem Wachstum nimmt der Holzbestand jährlich um 3,5 % zu. Er beträgt zu Beobachtungsbeginn 50 000 Festmeter.
Das Wachstum des Holzbestandes kann näherungsweise durch eine Funktion beschrieben werden.
beschrieben werden.
Berechne die Anzahl der Jahre, in denen sich der Holzbestand im Vergleich zum Beobachtungsbeginn verdoppelt hat.
Skizziere den Graphen von
Das Wachstum des Holzbestandes kann näherungsweise durch eine Funktion
Berechne die Anzahl der Jahre, in denen sich der Holzbestand im Vergleich zum Beobachtungsbeginn verdoppelt hat.
Skizziere den Graphen von
(4 BE)
2.
Der Förster weiß aus Erfahrung, dass 85 % aller Fichtensetzlinge anwachsen.
Er erhält eine Lieferung von 1 500 Fichtensetzlingen.
Er erhält eine Lieferung von 1 500 Fichtensetzlingen.
a)
Ermittle die zu erwartende Anzahl der Fichtensetzlinge, die nicht anwachsen.
Genau 5 dieser Fichtensetzlinge werden in einer Reihe nebeneinander gepflanzt.
(1 BE)
b)
Berechne die Wahrscheinlichkeiten folgender Ereignisse:
A:=
„Nur der erste und der zweite Fichtensetzling wachsen an.“
B:=
„Genau ein Fichtensetzling wächst nicht an.“
(2 BE)
c)
Formuliere das Gegenereignis zu: „Höchstens ein Fichtensetzling wächst nicht an.“
(1 BE)
1.
a)
Größe der Fläche mit Buchen berechnen
Die Fläche, die mit Buchen bepflanzt werden soll, wird durch ein rechtwinkliges Dreieck beschrieben. Dessen Flächeninhalt kann wie folgt berechnet werden:
![\(\begin{array}[t]{rll}
A_B&=& \dfrac{1}{2}\cdot \overline{AB}\cdot \overline{BC}\\[5pt]
&=& \dfrac{1}{2}\cdot 2\,100\,\text{m}\cdot 900\,\text{m}\\[5pt]
&=& 945\,000\,\text{m}^2
\end{array}\)](https://www.schullv.de/resources/formulas/071f5c4cdb7632d48ba15410f48d68609b5bff68f34a28499f22c79b32bf02e5_light.svg) Größe der Fläche mit Fichten nachweisen
Die Fläche des Fichtenteils wird durch das Dreieck
Größe der Fläche mit Fichten nachweisen
Die Fläche des Fichtenteils wird durch das Dreieck  beschrieben. Um dessen Flächeninhalt zu berechnen werden die Länge zweier Seitenlängen sowie die Größe eines eingeschlossenen Winkels benötigt.
beschrieben. Um dessen Flächeninhalt zu berechnen werden die Länge zweier Seitenlängen sowie die Größe eines eingeschlossenen Winkels benötigt.
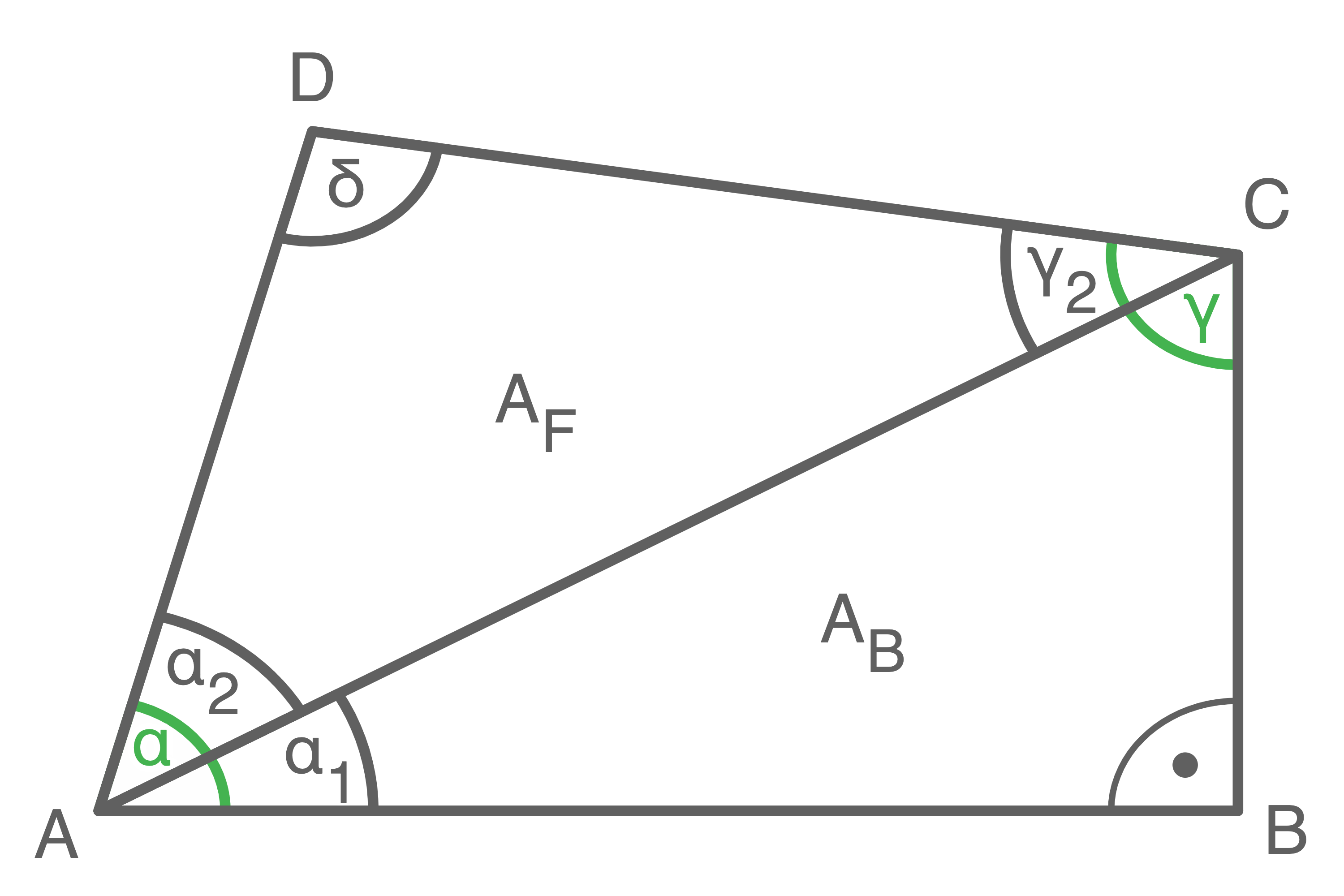 Zunächst wird die Größe des Winkels
Zunächst wird die Größe des Winkels  berechnet:
berechnet:
![\(\begin{array}[t]{rll}
\tan \alpha_1&=& \dfrac{\overline{BC}}{\overline{AB}} \\[5pt]
\tan \alpha_1&=& \dfrac{900\,\text{m}}{2\,100\,\text{m}} \quad \scriptsize \mid\; \tan^{-1} \\[5pt]
\alpha_1&\approx& 23,2^°
\end{array}\)](https://www.schullv.de/resources/formulas/6906a9b6f1adb748af80cb5a7ef8602c429a7f6e83bbca8e792efc3c3c8e2f19_light.svg) Wegen
Wegen  gilt:
gilt:
 Die Grundseite
Die Grundseite  kann über den Satz des Pythagoras berechnet werden:
kann über den Satz des Pythagoras berechnet werden:
![\(\begin{array}[t]{rll}
\overline{AC}^2&=& \overline{AB}^2+\overline{BC}^2 \\[5pt]
\overline{AC}^2&=&(2\,100\,\text{m})^2+(900\,\text{m})^2\\[5pt]
\overline{AC}^2&=& 5\,220\,000\,\text{m}^2 \quad \scriptsize \mid\;\sqrt{\,}\\[5pt]
\overline{AC}&\approx& 2\,284,7\,\text{m} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/86b4fae72d2f8fe6e690e82c693559138438252d8a7170c15162e23fb13bfc5b_light.svg) Die Seitenlänge
Die Seitenlänge  kann mit dem Sinussatz berechnet werden. Dazu werden noch die Größen der Winkel
kann mit dem Sinussatz berechnet werden. Dazu werden noch die Größen der Winkel  und
und  benötigt. Mit den Innenwinkelsummen des Dreiecks
benötigt. Mit den Innenwinkelsummen des Dreiecks  und des Vierecks
und des Vierecks  folgt:
folgt:
![\(\begin{array}[t]{rll}
\delta&=& 360^°-75^°-90^°-100^°&=& 95^°\\
\gamma_2&=& 180^°-51,8^°-95^°&=& 33,2^°
\end{array}\)](https://www.schullv.de/resources/formulas/1c9699704c6f9b71eb95d29afe20cc60b3765227b574d3ff006a009eb8f50048_light.svg) Mit dem Sinussatz folgt für die Länge der Strecke
Mit dem Sinussatz folgt für die Länge der Strecke 
![\(\begin{array}[t]{rll}
\dfrac{\overline{AD}}{\sin \gamma_2}&=& \dfrac{\overline{AC}}{\sin \delta} \quad \scriptsize \mid\;\cdot \sin \gamma_2 \\[5pt]
\overline{AD}&=& \dfrac{\overline{AC}}{\sin \delta}\cdot \sin \gamma_2 \\[5pt]
\overline{AD}&\approx& \dfrac{2\,284,7\,\text{m}}{\sin 95^°}\cdot \sin 33,2^° \\[5pt]
\overline{AD}&\approx& 1\,255,8\,\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/4a304dc04354e6b716cadadcc9fde4780ae4528e3b33658f440c53128a4b251d_light.svg) Damit lässt sich nun der Flächeninhalt des Dreiecks
Damit lässt sich nun der Flächeninhalt des Dreiecks  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
A_F&=& \dfrac{1}{2} \cdot \overline{AC} \cdot \overline{AD} \cdot \sin \alpha_2 \\[5pt]
&\approx& \dfrac{1}{2} \cdot 2\,284,7 \,\text{m} \cdot 1\,255,8 \,\text{m} \cdot \sin 51,8^° \\[5pt]
&\approx& 1\,127\,361 \,\text{m}^2 \\[5pt]
&\approx& 112,7\,\text{ha}
\end{array}\)](https://www.schullv.de/resources/formulas/04f381caf4965e95151a8959ad60cf2a1299a9d16f19319f13542bbd7dfdb9b4_light.svg) Damit ist nachgewiesen, dass die mit Fichten zu bepflanzende Fläche etwa 112,7 ha groß ist.
Damit ist nachgewiesen, dass die mit Fichten zu bepflanzende Fläche etwa 112,7 ha groß ist.

b)
Das Waldstück  hat mit Teilaufgabe a) einen Flächeninhalt von
hat mit Teilaufgabe a) einen Flächeninhalt von  Flächeninhalt des gesamten Waldstücks:
Flächeninhalt des gesamten Waldstücks:
 Anteil der mit Laubbäumen bedeckten Fläche:
Anteil der mit Laubbäumen bedeckten Fläche:
![\(\begin{array}[t]{rll}
\dfrac{p}{94,5\,\text{ha}}&=& \dfrac{100\,\%}{207,2\,\text{ha}} \quad \scriptsize \mid\;\cdot 94,5\,\text{ha}\\[5pt]
p&=& \dfrac{100\,\%}{207,2\,\text{ha}}\cdot 94,5\,\text{ha} \\[5pt]
p&=& 45,6\,\% \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/b6dd53e9da6744f37844417db5d157c1441a36120bdb5dd3c4045b5279ba6b0d_light.svg) Ein Vergleich mit den Angaben in der Aufgabenstellung zeigt, dass der Anteil an Laubbäumen etwas über dem in Deutschland üblichen Anteil liegt.
Ein Vergleich mit den Angaben in der Aufgabenstellung zeigt, dass der Anteil an Laubbäumen etwas über dem in Deutschland üblichen Anteil liegt.
c)
Zeit bis zur Verdoppelung berechnen
Das Wachstum des Holzbestandes kann durch eine Exponentialfunktion beschrieben werden. Die allgemeine Form dieser Funktion lautet  Dabei ist
Dabei ist  der Startwert,
der Startwert,  das jährliche Wachstum und
das jährliche Wachstum und  der Holzbestand nach
der Holzbestand nach  Jahren:
Jahren:
 Der Bestand hat sich verdoppelt, wenn er 100 000 Festmeter beträgt. Gesucht ist also die Lösung der Gleichung
Der Bestand hat sich verdoppelt, wenn er 100 000 Festmeter beträgt. Gesucht ist also die Lösung der Gleichung 
![\(\begin{array}[t]{rll}
100\,000\,\text{fm}&=& 50\,000\,\text{fm}\cdot 1,035^x \quad \scriptsize \mid\;:50\,000\,\text{fm} \\[5pt]
2&=& 1,035^x
\end{array}\)](https://www.schullv.de/resources/formulas/dd0d74d82c50686c979dfd5dd5008a3305dbe5c7cb5885e69d705a085bb095c3_light.svg) Mit dem Taschenrechner folgt
Mit dem Taschenrechner folgt  Nach etwas mehr als 20 Jahren hat sich der Holzbestand verdoppelt.
Graphen von
Nach etwas mehr als 20 Jahren hat sich der Holzbestand verdoppelt.
Graphen von  skizzieren
skizzieren
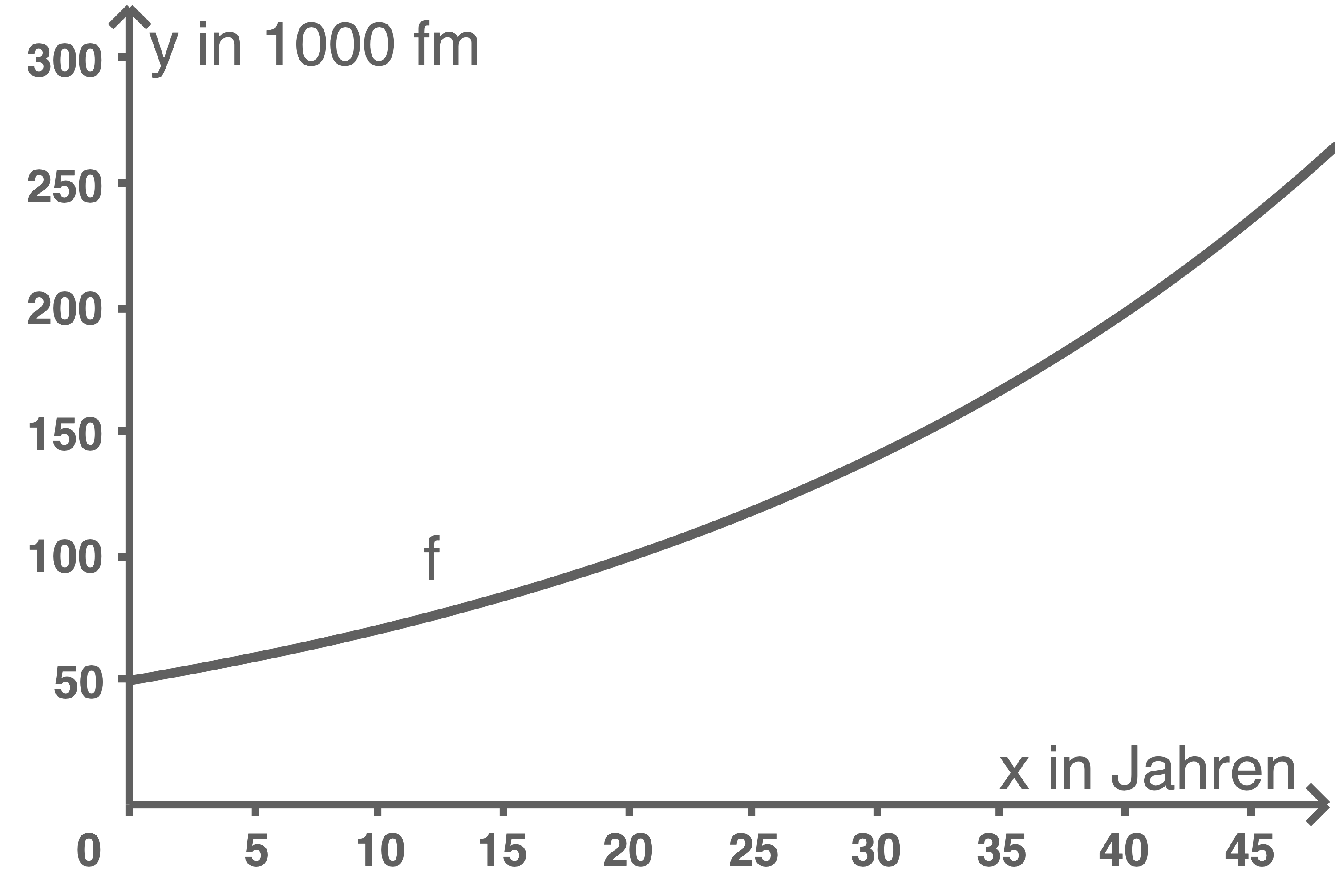

2.
a)
Die Wahrscheinlichkeit dafür, dass ein Setzling nicht anwächst, beträgt  Es werden
Es werden  Setzlinge eingepflanzt.
Setzlinge eingepflanzt.
 225 Setzlinge werden voraussichtlich nicht anwachsen.
225 Setzlinge werden voraussichtlich nicht anwachsen.
b)
Die Wahrscheinlichkeit, dass die ersten beiden Setzlinge anwachsen und die anderen drei nicht beträgt:
![\(\begin{array}[t]{rll}
P(A)&=& 0,85^2 \cdot 0,15^3\\[5pt]
&\approx& 0,0024
\end{array}\)](https://www.schullv.de/resources/formulas/7f4a3a0c7b198d3a6b787a9d60eac61984bbcf4c96012eab92709c17843025b5_light.svg) Es gibt 5 Möglichkeiten, dass genau ein Setzling nicht anwächst. Damit folgt:
Es gibt 5 Möglichkeiten, dass genau ein Setzling nicht anwächst. Damit folgt:
![\(\begin{array}[t]{rll}
P(B)&=& 5 \cdot 0,15 \cdot 0,85^4 \\[5pt]
&\approx& 0,3915
\end{array}\)](https://www.schullv.de/resources/formulas/831c52e42b695fa6d3584d1a07fa0ca4ceb606bff4ce2a2a4419bd8e877c4d1a_light.svg)
c)
Das Gegenereignis zu „Höchstens ein Fichtensetzling wächst nicht an“ ist gleichbedeutend zu „Mindestens vier Fichtensetzlinge wachsen an“. Das Gegenereignis lautet daher:
„Höchstens drei Fichtensetzlinge wachsen an.“