Wahlaufgabe 2
1.
Gegeben ist ein Quader 
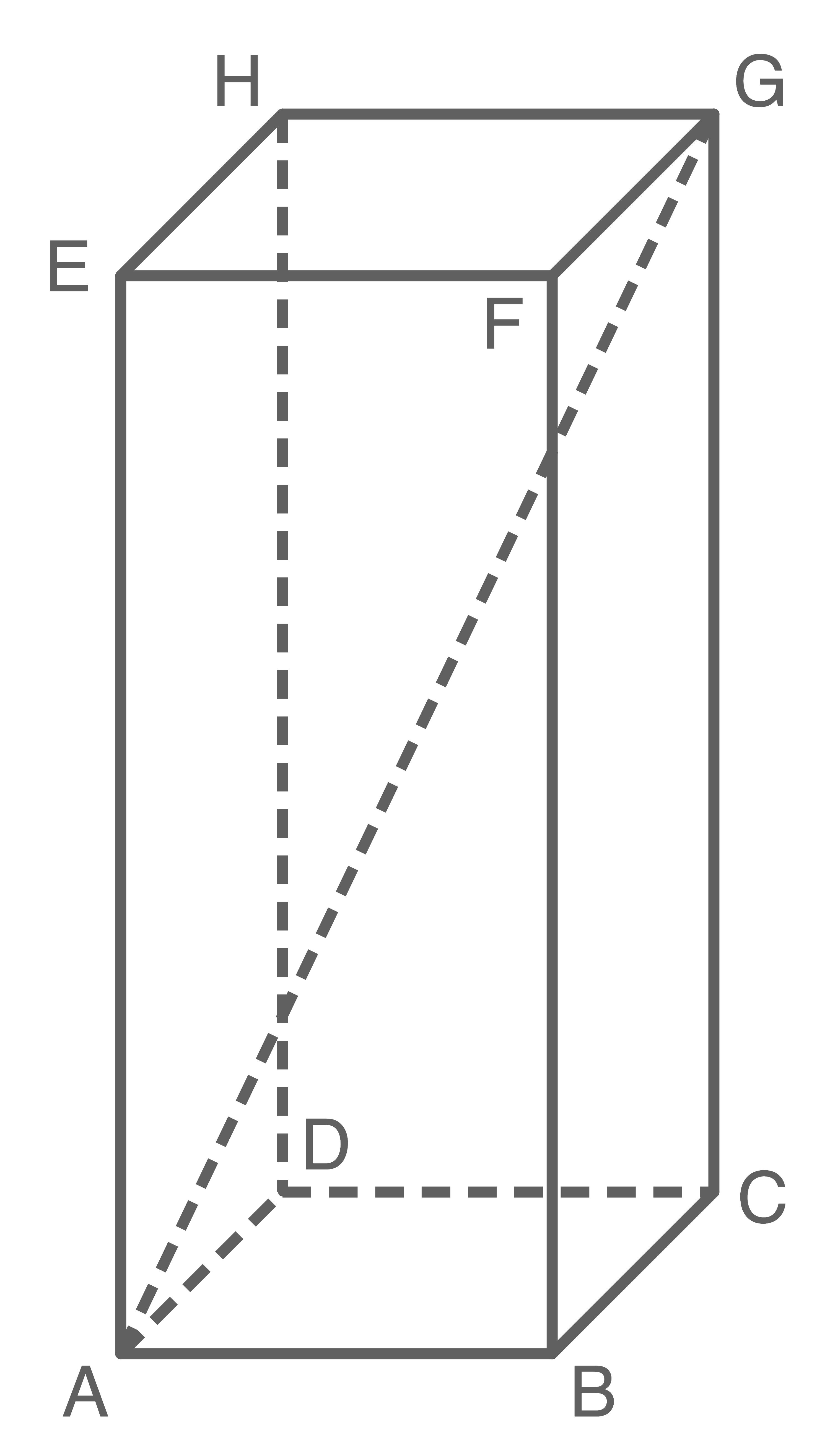
Skizze nicht maßstäblich
a)
Berechne die Höhe des Quaders.
(2 BE)
b)
Berechne die Größe des Winkels, den die Raumdiagonalen 
und 
einschließen.
(2 BE)
2.
In einem Springbrunnen befinden sich die Wasserdüsen in der Mitte.
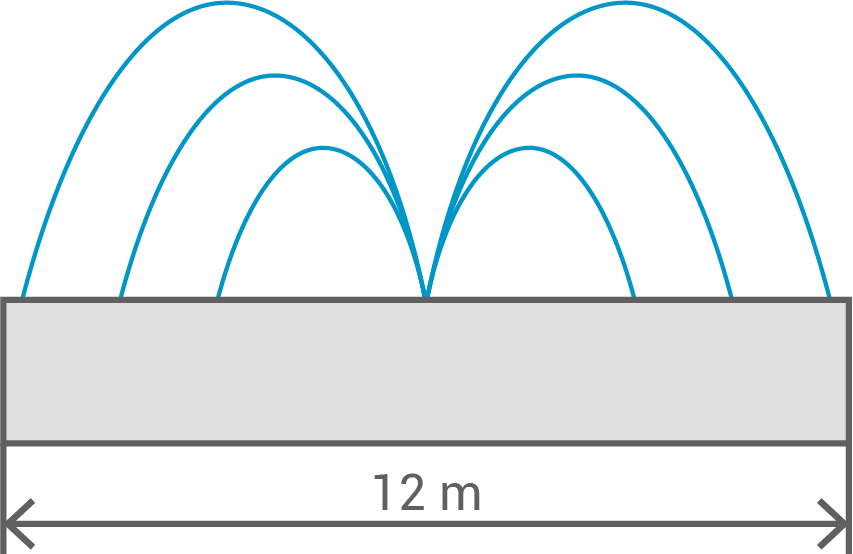
Die Fontänen dieses Springbrunnens können mathematisch durch die Gleichung
beschrieben werden.
Die Werte von
und 
sind Längen in Meter.
Skizze nicht maßstäblich
Die Fontänen dieses Springbrunnens können mathematisch durch die Gleichung
Die Werte von
a)
Gib zwei Werte von 
so an, dass zwei Fontänen beschrieben werden, die links der Wasserdüsen liegen.
Stelle die Funktionen für diese Werte von in einem geeigneten Koordinatensystem grapisch dar.
Stelle die Funktionen für diese Werte von
(2 BE)
b)
Es gibt Fontänen, die genau bis zum Rand des Springbrunnens reichen.
Berechne die maximale Höhe, die eine solche Fontäne erreicht.
Berechne die maximale Höhe, die eine solche Fontäne erreicht.
(2 BE)
c)
Ermittle einen Wert von so, dass die Funktionsgleichung eine 3 m hohe Fontäne mathematisch beschreibt.
(2 BE)
3.
Ein rotlackierter Holzquader, der 4 cm lang, 3 cm breit und 10 cm hoch ist, wird in Würfel mit jeweils 1 cm Kantenlänge zerteilt.
Diese Würfel werden in einem Stoffbeutel aufbewahrt. Ein Würfel wird zufällig gezogen und die Anzahl der roten Seitenflächen festgestellt.
Diese Würfel werden in einem Stoffbeutel aufbewahrt. Ein Würfel wird zufällig gezogen und die Anzahl der roten Seitenflächen festgestellt.
a)
Gib die Anzahl aller Würfel an.
(1 BE)
b)
Welche der folgenden Aussagen beschreiben ein sicheres Ereignis?
A := „Der gezogene Würfel hat weniger als vier rote Seitenflächen.“
B := „Der gezogene Würfel hat mindestens eine rote Seitenfläche.“
C := „Der gezogene Würfel hat höchstens drei rote Seitenflächen. “
(1 BE)
c)
Berechne die Wahrscheinlichkeiten folgender Ereignisse:
D := „Der gezogene Würfel hat drei rote Seitenflächen.“
E := „Der gezogene Würfel hat keine rote Seitenfläche.“
F := „Der gezogene Würfel hat höchstens zwei rote Seitenflächen.“
(3 BE)
1.
a)
Zunächst wird mit dem Satz des Pythagoras die Länge der Bodendiagonale berechnet:
![\(\begin{array}[t]{rll}
\overline{AB}\;^2+\overline{BC}\;^2&=&\overline{AC}\;^2 \quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
\sqrt{\overline{AB}\;^2+\overline{BC}\;^2}&=&\overline{AC} &\quad \scriptsize \\[5pt]
\sqrt{(4\;\text{cm})^2+({3\;\text{cm}})^2}&=&\overline{AC} &\quad \scriptsize \\[5pt]
5\;\text{cm} &=&\overline{AC}&\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/d58e34a74653e05d72855c078c72ad703676657f1ad87ba3ce27e80384fbc5a4?color=5a5a5a)
Damit kann nun ebenfalls mit dem Satz des Pythagoras die Höhe des Quaders berechnet werden:
![\(\begin{array}[t]{rll}
\overline{GC}^2+\overline{AC}^2&=&\overline{AG}^2 \quad \scriptsize \mid\;-\overline{AC}^2 \\[5pt]
\overline{GC}^2&=&\overline{AG}^2-\overline{AC}^2 \quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
\overline{GC}&=& \sqrt{\overline{AG}^2-\overline{AC}^2} &\quad \scriptsize \\[5pt]
\overline{GC}&=&\sqrt{(13\;\text{cm})^2-({5\;\text{cm}})^2} \\[5pt]
\overline{GC}&=& 12\;\text{cm} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/876efac29dc810ed4b62b047555ccc348453b0062b0633e5176490679d5cc1fd?color=5a5a5a)
Die Höhe des Quaders beträgt 
.
b)
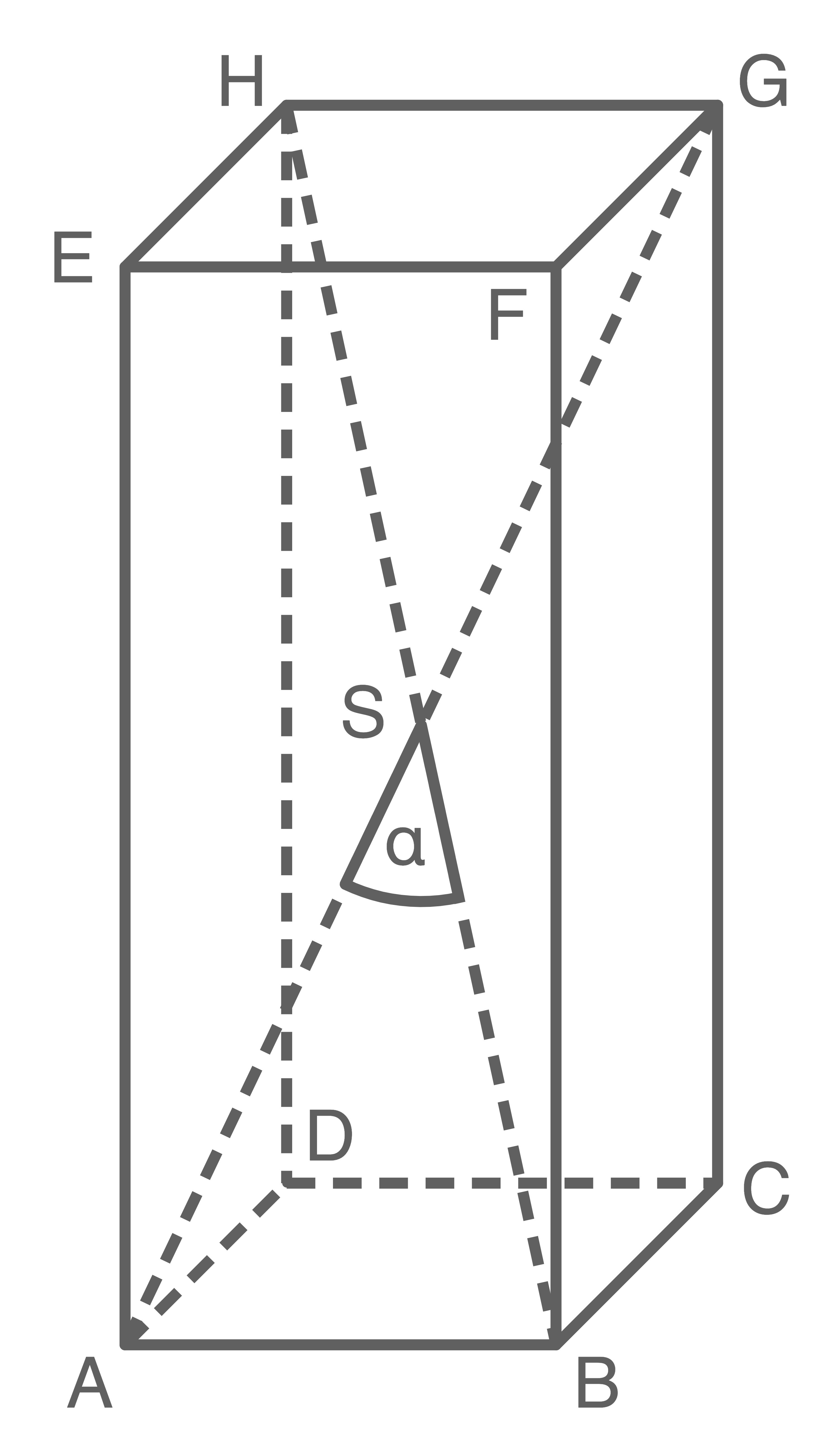
2.
a)
Zwei Werte von 
angeben
Die Funktionsgleichung lässt sich durch Ausklammern von 
wie folgt umformen:
Die Nullstellen sind also gegeben durch 
und 
Für 
liegt die Nullstelle also links vom Ursprung. Da zwischen den beiden äußeren Fontänen nach Aufgabenstellung 12 m liegen, muss 
gelten. Wegen 
muss daher 
mit 
gelten.
Für eine Fontäne links der Wasserdüsen muss insgesamt also 
gelten. Zwei mögliche Werte sind also 
und 
Funktionen darstellen
Graphen der Funktion mit und 
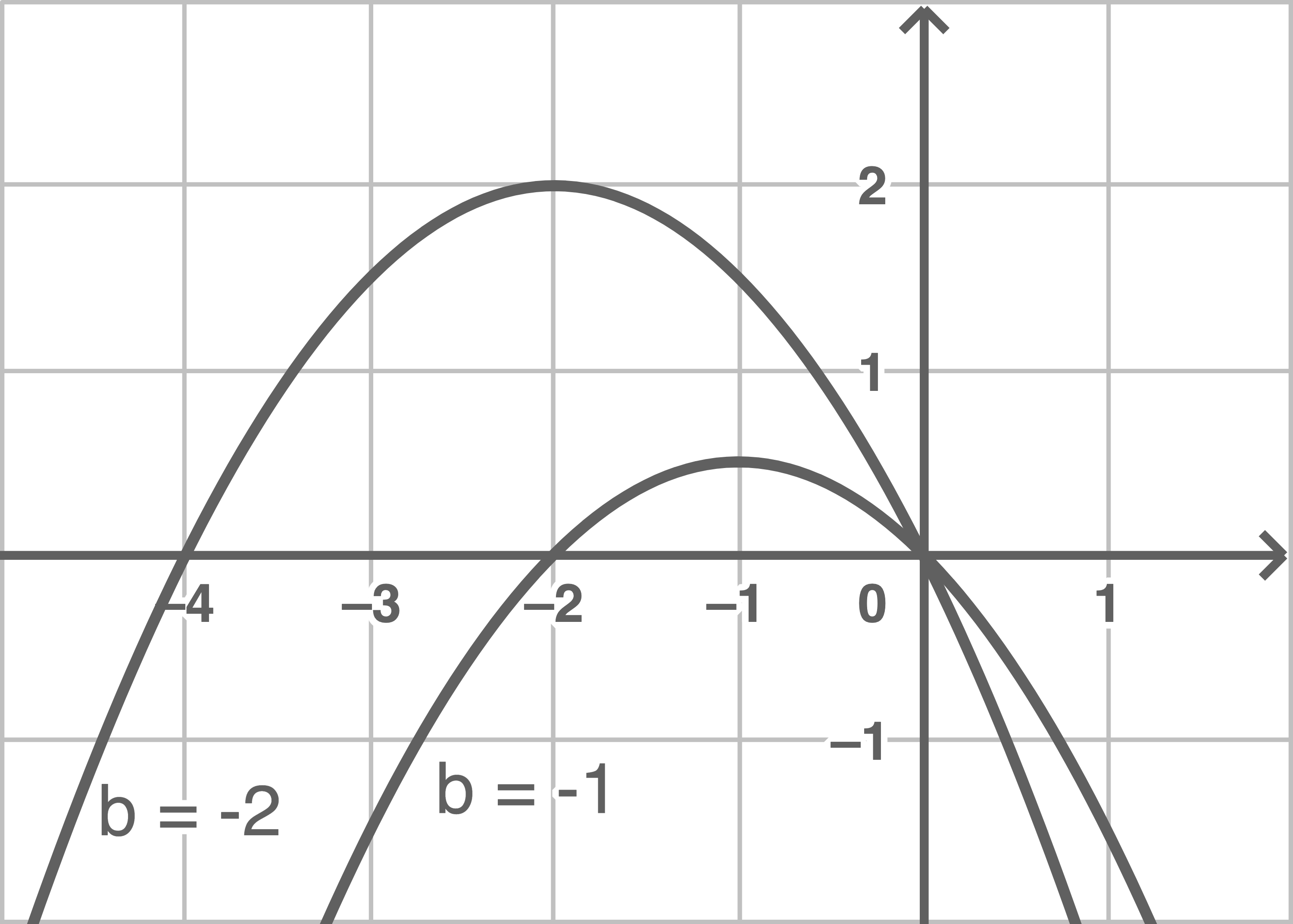
b)
Der Abstand von der Düse bis zum Rand beträgt auf einer Seite 6 m. Da die Nullstellen der Funktion durch und gegeben sind, muss der Parameter genau halb so groß mit 
und 
gewählt werden. Das Maximum befindet sich jeweils in der Mitte der beiden Nullstellen, also an den Stellen 
und 
Aus Symmetriegründen reicht es, den Funktionswert an einer der beiden Stellen zu berechnen. Einsetzen von liefert:
Die maximale Höhe einer Fontäne, die bis zum Rand des Springbrunnens reicht, beträgt 4,5 m.
c)
Das Maximum der Funktion liegt immer in der Mitte der Nullstellen 
und 
also an der Stelle 
Gesucht ist also die Lösung der Gleichung 
![\(\begin{array}[t]{rll}
-\dfrac{1}{2}b^2+b\cdot b&=& 3 \\[5pt]
\dfrac{1}{2}b^2&=& 3 \quad \scriptsize \mid\; \cdot 2 \\[5pt]
b^2&=& 6 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
b&=& \pm\sqrt{6}
\end{array}\)](https://mathjax.schullv.de/70f3b35229d559fb9eb194ca782052f1033c8159fb0f321d7e6f2aa15077443d?color=5a5a5a)
Für 
oder 
wird eine 3 m hohe Fontäne beschrieben.
3.
a)
Volumen des Holzquaders:
Volumen eines Würfels:
Anzahl der Würfel berechnen, die aus dem Holzquader herausgeschnitten werden können:
Es können 120 Würfel aus dem Holzquader herausgeschnitten werden.
b)
Aussage A beschreibt ein sicheres Ereignis, da ein Würfel höchstens drei rote Seitenflächen haben kann (von der Ecke des Quaders).
Aussage B beschreibt kein sicheres Ereignis, da es auch Würfel ohne rote Seitenflächen gibt (aus dem Inneren des Quaders).
Aussage C beschreibt analog zu Aussage A ein sicheres Ereignis.
c)
D:
Es gibt insgesamt 8 Würfel mit 3 roten Seitenflächen: die Würfel, die aus den Ecken des Quaders geschnitten wurden.
E:
Die Anzahl der Würfel, die keine rote Seitenflächen haben, sind die aus dem Inneren des Quaders. Dieses Innere ist wieder ein Quader, der auf jeder Seite eine Würfelschicht weniger als der ursprüngliche Quader hat. Für jede Seitenlänge hat der innere Quader also insgesamt zwei Würfelschichten weniger. Die Anzahl der Würfel ohne rote Seitenflächen kann daher wie folgt berechnet werden:
Es gibt also insgesamt 16 Würfel ohne roten Rand.
F:
Dies ist das Gegenereignis zum Ereignis 
, somit gilt:
