Wahlaufgabe 2
1.
Gegeben ist die Funktion  durch
durch  in ihrem größtmöglichen Definitionsbereich.
in ihrem größtmöglichen Definitionsbereich.
 eine Funktion
eine Funktion  durch
durch  .
.
a)
Gib den Definitionsbereich und zwei weitere Eigenschaften der Funktion  an.
an.
(3 BE)
b)
Berechne die Stelle, an der der Funktionswert 2015 beträgt.
Gegeben ist für jede reelle Zahl
(1 BE)
c)
Weise nach, dass für  die Graphen von
die Graphen von  und
und  genau einen gemeinsamen Punkt haben.
genau einen gemeinsamen Punkt haben.
Es gibt einen weiteren Wert für so, dass die Graphen von
so, dass die Graphen von  und
und  genau einen gemeinsamen Punkt haben. Gib diesen Wert an.
genau einen gemeinsamen Punkt haben. Gib diesen Wert an.
Es gibt einen weiteren Wert für
(2 BE)
d)
Gib die Gleichung einer Funktion  so an, dass die Graphen von
so an, dass die Graphen von  und
und  zwei gemeinsame Punkte haben.
zwei gemeinsame Punkte haben.
(1 BE)
2.
Gegeben ist das Netz eines regelmäßigen Tetraeders, dessen Flächen mit 1, 2, 3 und 4 beschriftet sind. Wird der Tetraeder geworfen, so ist der Versuchsausgang die Zahl, auf der der Tetraeder liegt.
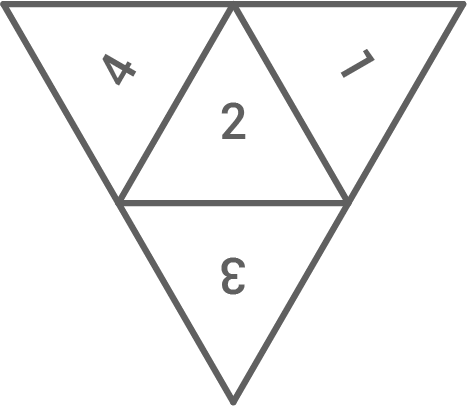
a)
Berechne die Wahrscheinlichkeiten folgender Ereignisse:
„Beim zweimaligen Werfen des Tetraeders fällt zweimal die 1.“
„Beim zweimaligen Werfen des Tetraeders ist die Summe der Augenzahlen durch zwei teilbar.“
„Beim achtmaligen Werfen fällt mindestens einmal die 1.“
(3 BE)
b)
Bei einem Spiel darf der Tetraeder für einen Einsatz von 2 € einmal geworfen werden. Den Betrag, der der geworfenen Zahl entspricht, bekommt man in Euro ausgezahlt.
Untersuche, ob man bei diesem Spiel auf lange Sicht gewinnt oder verliert.
Untersuche, ob man bei diesem Spiel auf lange Sicht gewinnt oder verliert.
(2 BE)
3.
Im Mathematikunterricht der Klasse  soll für ein Dreieck
soll für ein Dreieck  von dem
von dem  ,
,  ,
,  bekannt sind, die Größe des Winkels
bekannt sind, die Größe des Winkels  bestimmt werden. Anna führt eine Konstruktion mit einem Geometrieprogramm durch und erhält
bestimmt werden. Anna führt eine Konstruktion mit einem Geometrieprogramm durch und erhält  Max berechnet für die Größe des Winkels
Max berechnet für die Größe des Winkels  Beurteile beide Ergebnisse.
Beurteile beide Ergebnisse.
(3 BE)
1.
a)
Definitionsbereich angeben
 ist in gesamt
ist in gesamt  definiert, bis auf die Stelle, an der der Nenner null wird. Das ist für
definiert, bis auf die Stelle, an der der Nenner null wird. Das ist für  der Fall. Somit ist der Definitionsbereich
der Fall. Somit ist der Definitionsbereich  .
Zwei weitere Eigenschaften angeben
Es gibt mehrere mögliche Eigenschaften:
.
Zwei weitere Eigenschaften angeben
Es gibt mehrere mögliche Eigenschaften:
für
hat keine Nullstellen
ist streng monoton fallend
b)
Gesucht ist die Lösung der Gleichung 
![\(\begin{array}[t]{rll}
f(x)&=& 2\,015 \\[5pt]
\dfrac{1}{x-2}&=& 2\,015 \quad \scriptsize\mid\; \cdot (x-2) \\[5pt]
1&=& 2\,015\cdot (x-2) \\[5pt]
1&=& 2\,015\cdot x - 4\,030 \quad\scriptsize\mid\; +4\,030 \\[5pt]
4\,031 &=& 2\,015\cdot x \quad \scriptsize\mid\; :2\,015 \\[5pt]
\dfrac{4\,031}{2\,015} &=& x
\end{array}\)](https://www.schullv.de/resources/formulas/4d7e8aea65b2886882b13d7e7b28bf01b55efe1f2eec10ac6b48e23826e489a2_light.svg) An der Stelle
An der Stelle  beträgt der Funktionswert
beträgt der Funktionswert 
c)
Gemeinsamen Punkt nachweisen
Es gibt dann genau einen gemeinsamen Schnittpunkt, wenn die Gleichung  genau eine Lösung hat.
genau eine Lösung hat.
![\(\begin{array}[t]{rll}
f(x)&=& g(x) \\[5pt]
\dfrac{1}{x-2}&=& -x+4
\end{array}\)](https://www.schullv.de/resources/formulas/e6b5e9c6d34ffe7e9e2f13b83841d2405c02eff330acd02dc0af5bb954703f3f_light.svg) Der Taschenrechner liefert die einzige Lösung
Der Taschenrechner liefert die einzige Lösung  somit gibt es genau einen gemeinsamen Punkt.
Wert für
somit gibt es genau einen gemeinsamen Punkt.
Wert für  angeben
Für einen weiteren Wert von
angeben
Für einen weiteren Wert von  haben die Graphen der beiden Funktionen genau einen gemeinsamen Schnittpunkt. Beim Gleichsetzen der beiden Funktionen liefert der Taschenrechner jedoch eine schwer auszuwertende Lösung. Graphisch lässt sich die Lösung dagegen schnell ermitteln:
haben die Graphen der beiden Funktionen genau einen gemeinsamen Schnittpunkt. Beim Gleichsetzen der beiden Funktionen liefert der Taschenrechner jedoch eine schwer auszuwertende Lösung. Graphisch lässt sich die Lösung dagegen schnell ermitteln:


Der Schnittpunkt des Graphen der Funktion  schneidet den Graphen der Funktion
schneidet den Graphen der Funktion  nur im Punkt
nur im Punkt  Die einzige andere Parallele zu
Die einzige andere Parallele zu  die den Graphen von
die den Graphen von  in genau einem Punkt schneidet, muss durch den Punkt
in genau einem Punkt schneidet, muss durch den Punkt  gehen.
Die zugehörige Funktionsgleichung lautet
gehen.
Die zugehörige Funktionsgleichung lautet  daher ist der gesuchte Wert
daher ist der gesuchte Wert 
d)
Laut Teilaufgabe a) gibt es für die Werte von  und
und  genau einen gemeinsamen Schnittpunkt der Graphen von
genau einen gemeinsamen Schnittpunkt der Graphen von  und
und  Der graphischen Darstellung lässt sich entnehmen, dass es für die Werte
Der graphischen Darstellung lässt sich entnehmen, dass es für die Werte  und
und  jeweils zwei Schnittpunkte gibt.
Eine mögliche Funktionsgleichung lautet daher
jeweils zwei Schnittpunkte gibt.
Eine mögliche Funktionsgleichung lautet daher 
2.
a)
Das Werfen des Tetraeders ist ein Laplace-Experiment, daher gilt 
![\(\begin{array}[t]{rll}
P(A)&=& P(1)\cdot P(1) \\[5pt]
&=& \dfrac{1}{4}\cdot \dfrac{1}{4} \\[5pt]
&=& \dfrac{1}{16}
\end{array}\)](https://www.schullv.de/resources/formulas/0ff553ae124f1a1c18527ff7c7b7bc184458e74595bec1d15c90596a8d7abe2f_light.svg)
![\(\begin{array}[t]{rll}
P(B)&=& P(11;\,13;\,22;\,24;\,31;\,33;\,42;\,44) \\[5pt]
&=& 8\cdot \dfrac{1}{4}\cdot \dfrac{1}{4} \\[5pt]
&=& \dfrac{1}{2}
\end{array}\)](https://www.schullv.de/resources/formulas/cdaf2d5020cada988234bc14f81dd5c76f50a50d450f493328e8864ca6c53ad7_light.svg)
![\(\begin{array}[t]{rll}
P(C)&=& 1-P(\overline{C}) \\[5pt]
&=& 1-\left(\dfrac{3}{4}\right)^8 \\[5pt]
&\approx& 0,8999
\end{array}\)](https://www.schullv.de/resources/formulas/a1298bc141f27d87c3f151e646c35533a1ad403f991541b2c4080914ff421ff5_light.svg)
b)
3.
Die Größe des Winkels  lässt sich mit dem Sinussatz berechnen:
lässt sich mit dem Sinussatz berechnen:
![\(\begin{array}[t]{rll}
\dfrac{b}{\sin\;\beta}&=&\dfrac{c}{\sin\;\gamma} \\[5pt]
\dfrac{4}{\sin(30^{\circ})}&=& \dfrac{6}{\sin\;\gamma} \\[5pt]
8 &=& \dfrac{6}{\sin\;\gamma} \quad \scriptsize \mid \; \cdot \sin \gamma \\[5pt]
8\cdot \sin \gamma &=& 6 \quad \scriptsize \mid\; :8 \\[5pt]
\sin \gamma &=& \dfrac{3}{4} \quad \scriptsize \mid \; \sin^{-1} \\[5pt]
\gamma_1&\approx& 131,4^{\circ} \\[5pt]
\gamma_2&\approx& 48,5^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/4e3543d1ae8afd49f982bf17cc21935586131b1316422755d4eb17ebdb5497e1_light.svg) Es sind also beide Winkelgrößen möglich. Das Dreieck ist durch die gegebenen Informationen nicht eindeutig.
Es sind also beide Winkelgrößen möglich. Das Dreieck ist durch die gegebenen Informationen nicht eindeutig.