Pflichtaufgabe 2 – Mit Hilfsmitteln

Beim Werfen eines Bausteins sind folgende Ergebnisse möglich.

$A:=\,$ „Der Stein liegt auf den Noppen.“

$B:=\,$ „Der Stein liegt auf einer Seitenfläche.“

$C:=\,$ „Der Stein liegt auf der Unterseite.“

Für 200 Würfe erfasste Leon folgende Daten:

Ergebnis	$A$	$B$	$C$
absolute Häufigkeit	$97$	$\,$	$43$

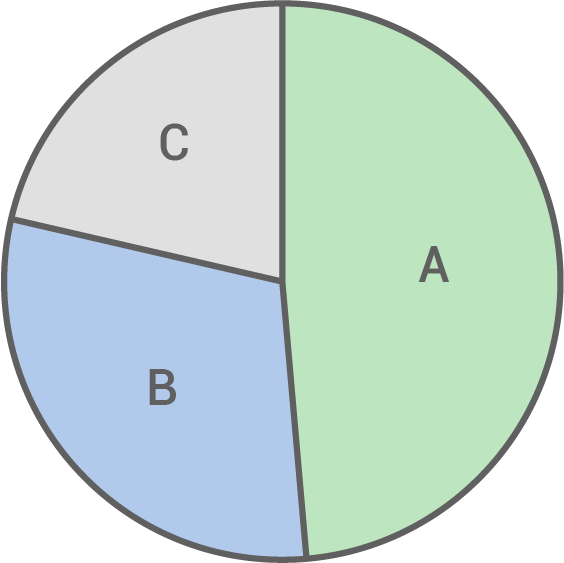
Stelle die Ergebnisse in einem Kreisdiagramm dar.

(3 BE)

Hannah beschreibt die Wahrscheinlichkeitsverteilung für diesen Baustein durch:

Ergebnis	$A$	$B$	$C$
Wahrscheinlichkeit	$0,5$	$0,3$	$0,2$

Dieser Baustein wird zweimal geworfen.

Formuliere ein Ereignis in Worten, dessen Wahrscheinlichkeit mit $p=2\cdot 0,5\cdot 0,3$ berechnet werden kann.

(2 BE)

Berechne die Wahrscheinlichkeit dafür, dass dieser Baustein mindestens einmal auf der Unterseite liegen bleibt.

(2 BE)

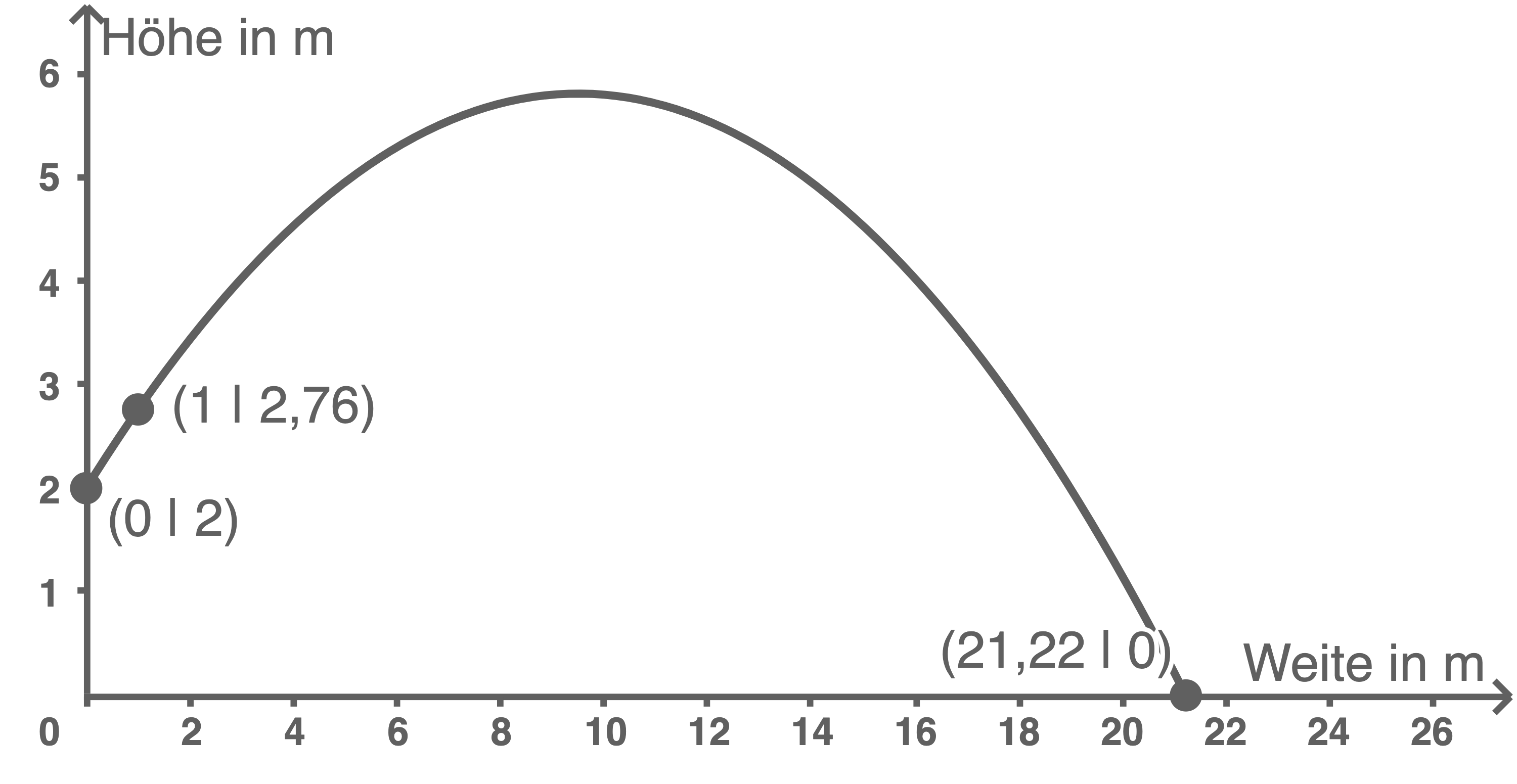
Bei einem Wettkampf in Göteburg erzielte im Jahr 1995 die Kugelstoßerin Astrid Kumbernuss die Weite von 21,22 m. Die Höhe, in der die Kugel bei diesem Versuch ihre Hand verließ, betrug zwei Meter. In einem Meter Abstand vom Abstoß in horizontaler Richtung hatte die Kugel eine Höhe von 2,76 m. Die Flugbahn der Kugel kann mathematisch durch eine quadratische Parabel beschrieben werden.

Skizziere diesen Sachverhalt in einem geeigneten Koordinatensystem.

(2 BE)

Weise rechnerisch nach, dass die Kugel nicht über 6,00 m steigt.

(4 BE)

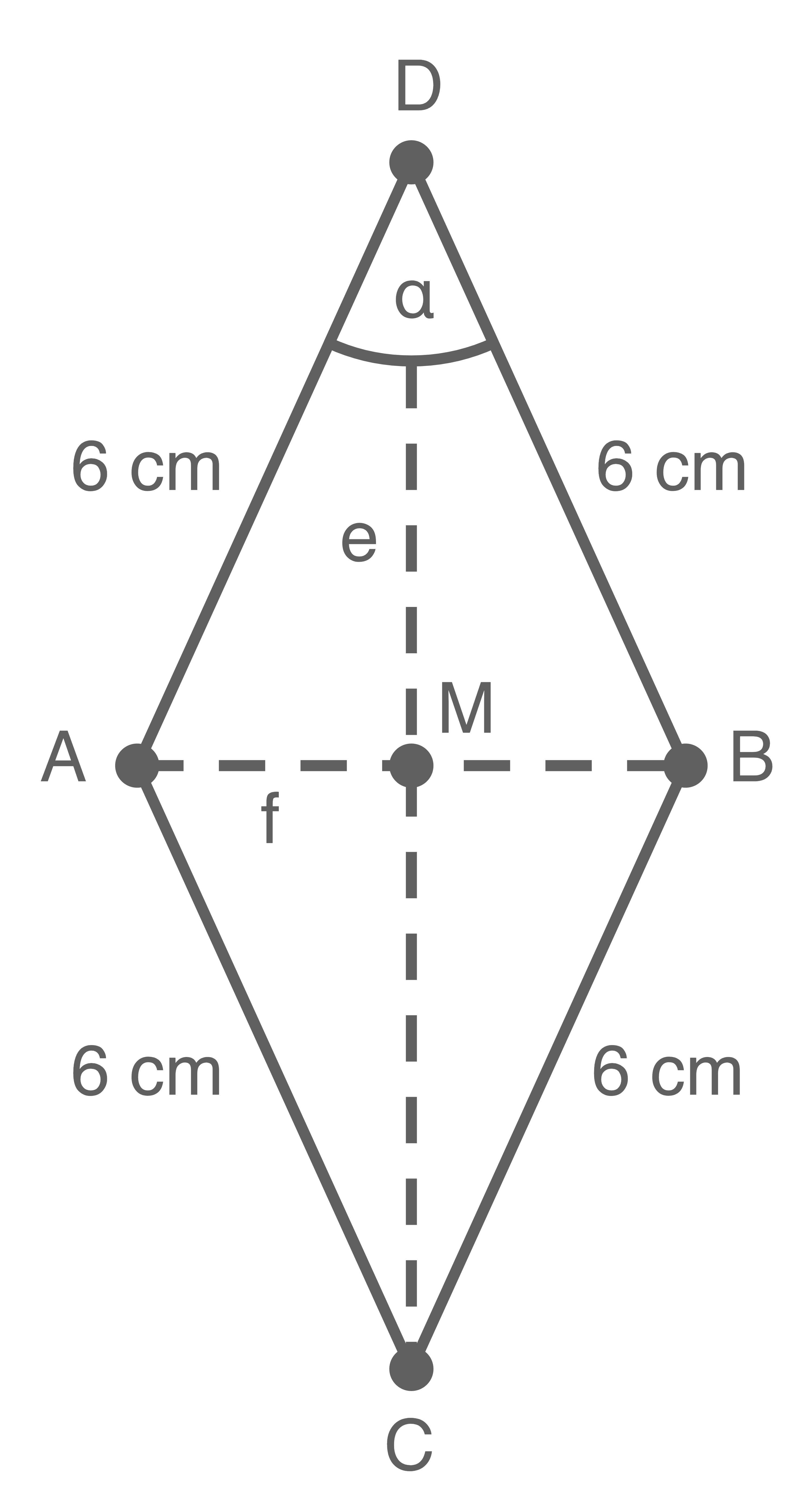
Gegeben ist ein Rhombus mit der Seitenlänge 6,0 cm und einem Innenwinkel $\alpha.$

Berechne die Länge einer Diagonalen und den Flächeninhalt des Rhombus für $\alpha=50^{\circ}$ .

(4 BE)

Beschreibe den Einfluss des Winkels $\alpha$ auf die Größe des Flächeninhaltes vom Rhombus.

(3 BE)

Zunächst muss die Tabelle um den fehlenden Wert ergänzt werden.

$200-97-43=60$

Ergebnis	$A$	$B$	$C$
absolute Häufigkeit	$97$	$60$	$43$

Winkelberechnungen:

$A:\quad\dfrac{97}{200}\cdot360^\circ\approx 175^\circ$

$B:\quad\dfrac{60}{200}\cdot360^\circ\approx 108^\circ$

$C:\quad\dfrac{43}{200}\cdot360^\circ\approx 77^\circ$

Der Baustein liegt genau einmal auf den Noppen und genau einmal auf einer Seitenfläche.

Die Wahrscheinlichkeit für das Ereignis $E:=$ „Der Baustein bleibt bei zwei Würfen mindestens einmal auf der Unterseite liegen“ kann über das Gegenereignis berechnet werden. Dieses lautet:

$\overline{E}:=$ „Der Baustein bleibt bei keinem der Würfe auf der Unterseite liegen.“

Die Wahrscheinlichkeit dafür, dass der Baustein bei einem Wurf nicht auf der Unterseite landet, beträgt $1-0,2=0,8.$ Damit folgt:

$P(\overline{E})=0,8\cdot 0,8=0,64$

Für die gesuchte Wahrscheinlichkeit folgt dann:

$P(E)=1-P(\overline{E})=1-0,64=0,36$

Zunächst muss die Funktionsgleichung der Parabel berechnet werden. Die allgemeine Form einer quadratischen Parabel lautet $p(x)= a\cdot (x-b)^2+c.$ Einsetzen der Koordinaten der drei bekannten Punkte $(0\mid 2),$ $(1\mid 2,76)$ und $(21,22 \mid 0)$ liefert das folgende Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad& 2 &=& p (0) \\ & 2 &=& a\cdot (0-b)^2+c \\[5pt] & 2 &=& a\cdot b^2+c \\[5pt] \text{II}\quad& 2,76 &=& p(1) \\ & 2,76 &=& a\cdot (1-b)^2+c \\[5pt] \text{III}\quad& 0 &=& p(21,22) \\ & 0 &=& a\cdot (21,22-b)^2+c \\ \end{array}$

Der Taschenrechner liefert folgende Lösung:

$a \approx -0,04,\quad$ $b\approx 9,49,\quad$ $c\approx 5,81$

Die Gleichung der Parabel lautet also:

$p(x) = -0,04\cdot (x-9,49)^2 +5,81$

Der Scheitelpunkt der Parabel hat also ungefähr die Koordinaten $S(9,49\mid 5,81).$ Da dieser den höchsten Punkt der Flugbahn beschreibt und $5,81 \lt 6,00$ ist, fliegt die Kugel nicht höher als $6,00\,\text{m}.$

Länge einer Diagonalen berechnen

Im Folgenden wird die Länge beider Diagonalen berechnet. Gefragt ist jedoch nur die Länge einer Diagonalen.

$\begin{array}[t]{rll} \sin\left(\dfrac{\alpha}{2}\right)&=& \dfrac{\frac{f}{2}}{6\,\text{cm}} \\[5pt] \sin(25°)&=& \dfrac{f}{12\,\text{cm}} \quad \scriptsize \mid\;\cdot 12\,\text{cm}\\[5pt] 5,1 \,\text{cm}&\approx& f \end{array}$

$\begin{array}[t]{rll} \cos\left(\dfrac{\alpha}{2}\right)&=& \dfrac{\frac{e}{2}}{6\,\text{cm}} \\[5pt] \cos(25°)&=& \dfrac{e}{12\,\text{cm}} \quad \scriptsize \mid\;\cdot 12\,\text{cm}\\[5pt] 10,9 \,\text{cm}&\approx& e \end{array}$

Flächeninhalt berechnen

Mit der Formel für den Flächeninhalt eines Rhombus gilt:

$\begin{array}[t]{rll} A&=& a^2\cdot \sin(\alpha) \\[5pt] &=& (6\,\text{cm})^2\cdot \sin(50°) \\[5pt] &\approx& 27,6\,\text{cm}^2 \end{array}$

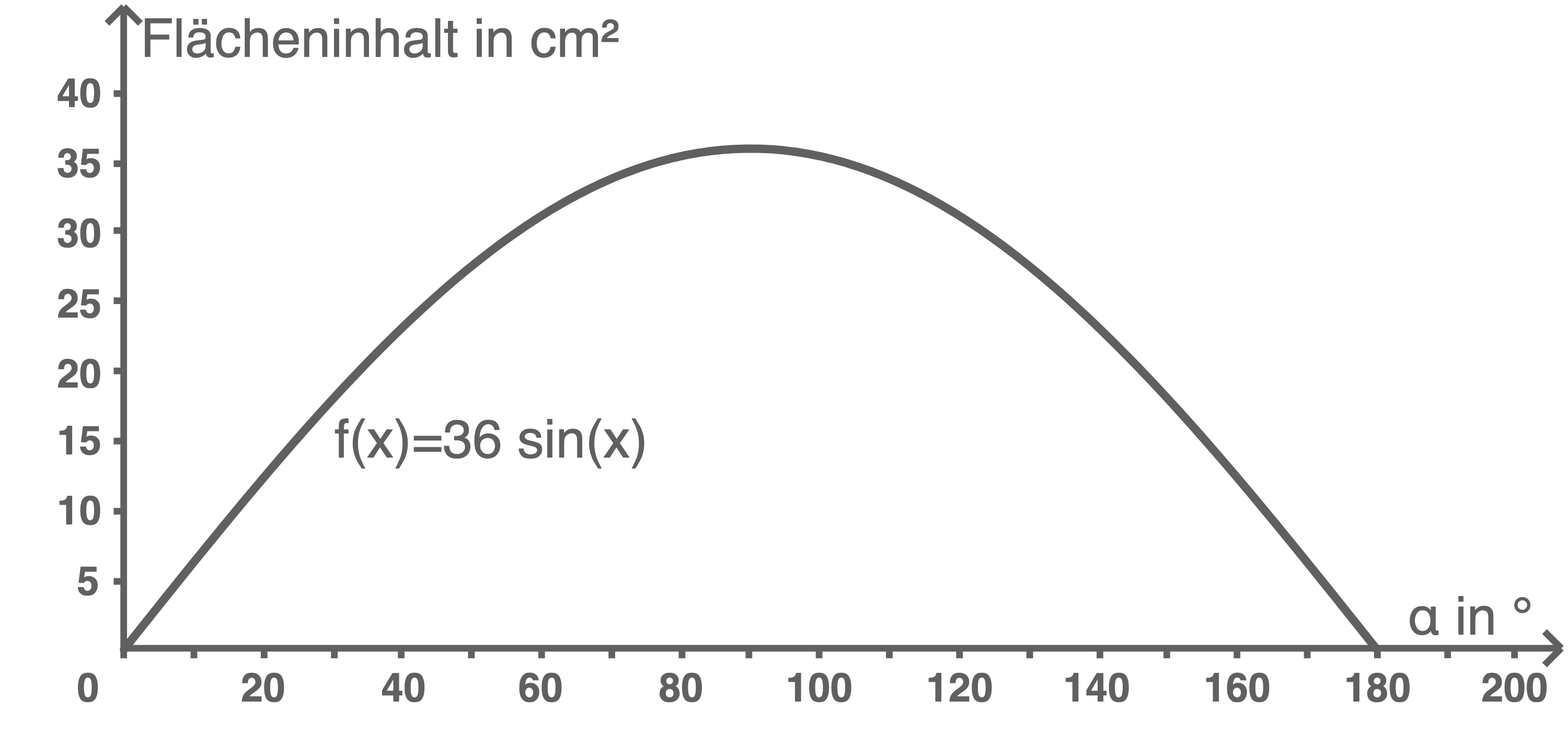
Der Flächeninhalt des Rhombus lässt sich mit der Formel $A=a^2\cdot \sin(\alpha)$ berechnen. Da $\alpha$ ein Innenwinkel ist, muss $0°\lt \alpha \lt 180°$ gelten. In diesem Intervall gilt für $\sin(\alpha):$

Für $\alpha=90^°$ ist der Wert von $\sin(\alpha)$ am höchsten und der Flächeninhalt damit am größten.

Je weiter der Winkel $\alpha$ sich dem Wert $\alpha=180°$ oder $\alpha=0°$ nähert, desto kleiner wird der Wert von $\sin(\alpha)$ und damit auch der Flächeninhalt des Rhombus.

Für den Wert $a=6\,\text{cm}$ aus der Aufgabenstellung ist die Größe des Flächeninhalt in Abhängigkeit vom Winkel $\alpha$ dargestellt: