Pflichtaufgabe 2 – Mit Hilfsmitteln
1.
Gegeben ist die Funktion 
durch 
a)
Gib den Wertebereich und zwei weitere Eigenschaften der Funktion an.
(3 BE)
b)
Ermittle die Schnittstellen des Graphen der Funktion mit dem Graphen von 
(1 BE)
c)
Für jede natürliche Zahl 
ist die Funktion 
gegeben durch 
Gib jeweils alle Werte für so an, dass:
I
der Graph von im gesamten Definitionsbereich monoton fallend ist.
II
die Graphen von und 
mit 
keinen Punkt gemeinsam haben.
(2 BE)
2.
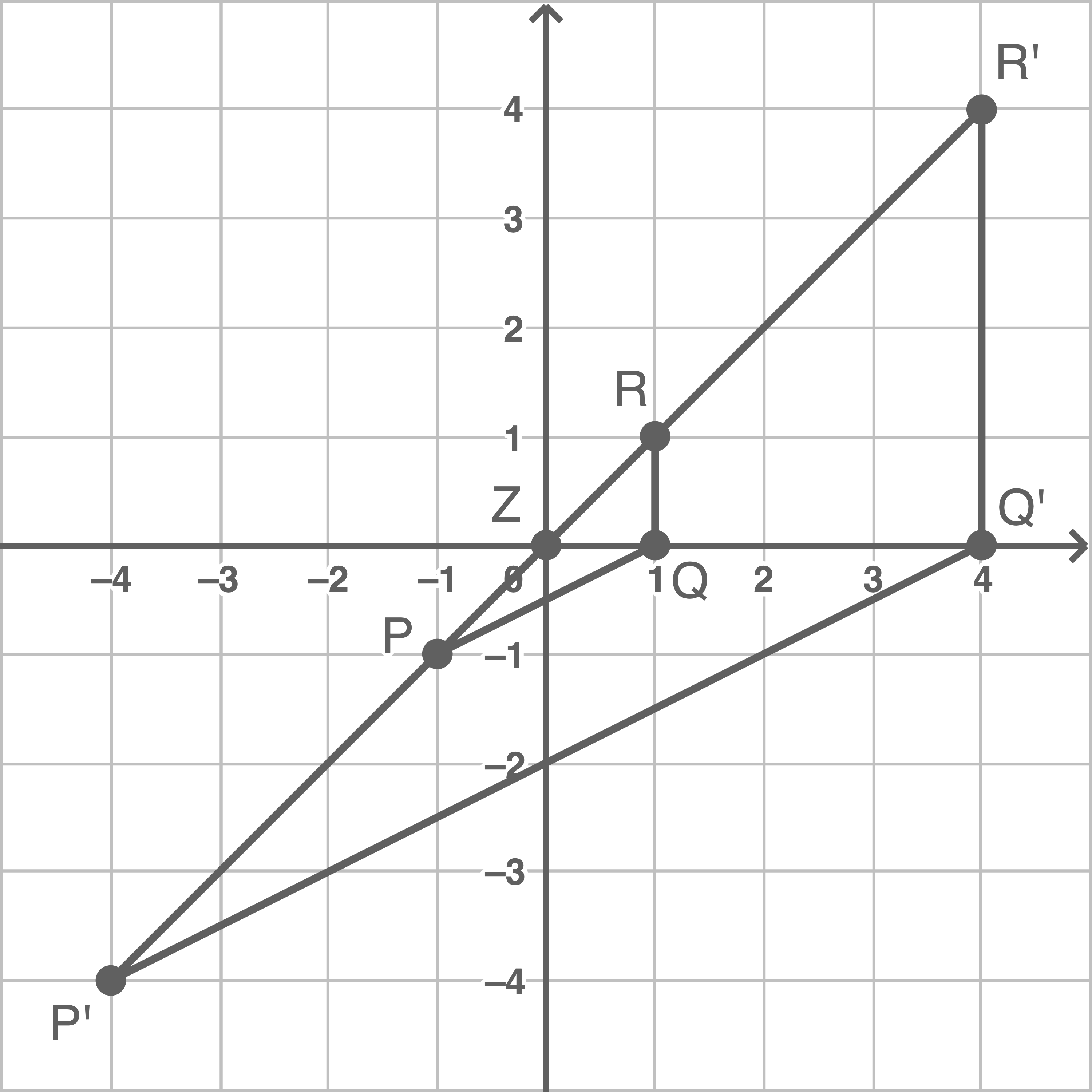
Die Punkte 
, 
und 
bilden ein Dreieck. Durch zentrische Streckung des Dreiecks 
mit dem Streckungszentrum 
und dem Streckfaktor 
entsteht das Dreieck 
a)
Zeichne die Dreiecke und 
in ein Koordinatensystem.
(2 BE)
b)
Bestimme die Flächeninhalte beider Dreiecke.
(2 BE)
3.
Ein Glücksrad (siehe Skizze) wird dreimal gedreht. Der Spieleinsatz beträgt dafür ein Euro.
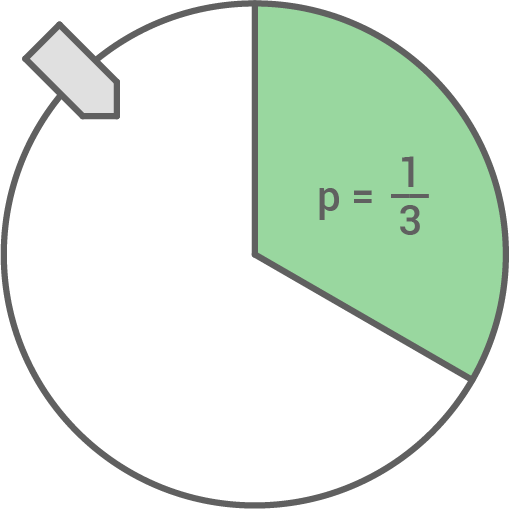
Bleibt der Zeiger genau einmal auf dem grünen Feld stehen, wird ein Euro ausgezahlt.
Bei „genau zweimal grün“ werden zwei Euro, bei „dreimal grün“ sechs Euro ausgezahlt.
Bleibt der Zeiger genau einmal auf dem grünen Feld stehen, wird ein Euro ausgezahlt.
Bei „genau zweimal grün“ werden zwei Euro, bei „dreimal grün“ sechs Euro ausgezahlt.
a)
Zeichne ein vollständig beschriftetes Baumdiagramm.
(1 BE)
b)
Ermittle die Wahrscheinlichkeit dafür, dass man bei diesem Spiel weder Geld gewinnt noch verliert.
(1 BE)
c)
Untersuche, ob auf lange Sicht ein Gewinn zu erwarten ist.
(3 BE)
1.
a)
Wertebereich angeben
Da der erste Summand immer größer als null ist, gilt für den Wertebereich von 
Weitere Eigenschaften von 
angeben
Es können beispielsweise folgende Eigenschaften von angegeben werden:
- Der Graph von
und
- Der Graph ist achsensymmetrisch zur Geraden
- Für
ist die Funktion streng monoton steigend, für
ist sie streng monoton fallend.
b)
Gesucht ist die Lösung der Gleichung 
Der Taschenrechner liefert die Schnittstellen 
und 
.
c)
I
Der Graph ist im gesamten Definitionsbereich monoton fallend, wenn die Werte für ungerade sind.
II
Die Graphen von und haben keine gemeinsamen Punkte, wenn die Werte für gerade sind und 
gilt.
2.
a)
b)
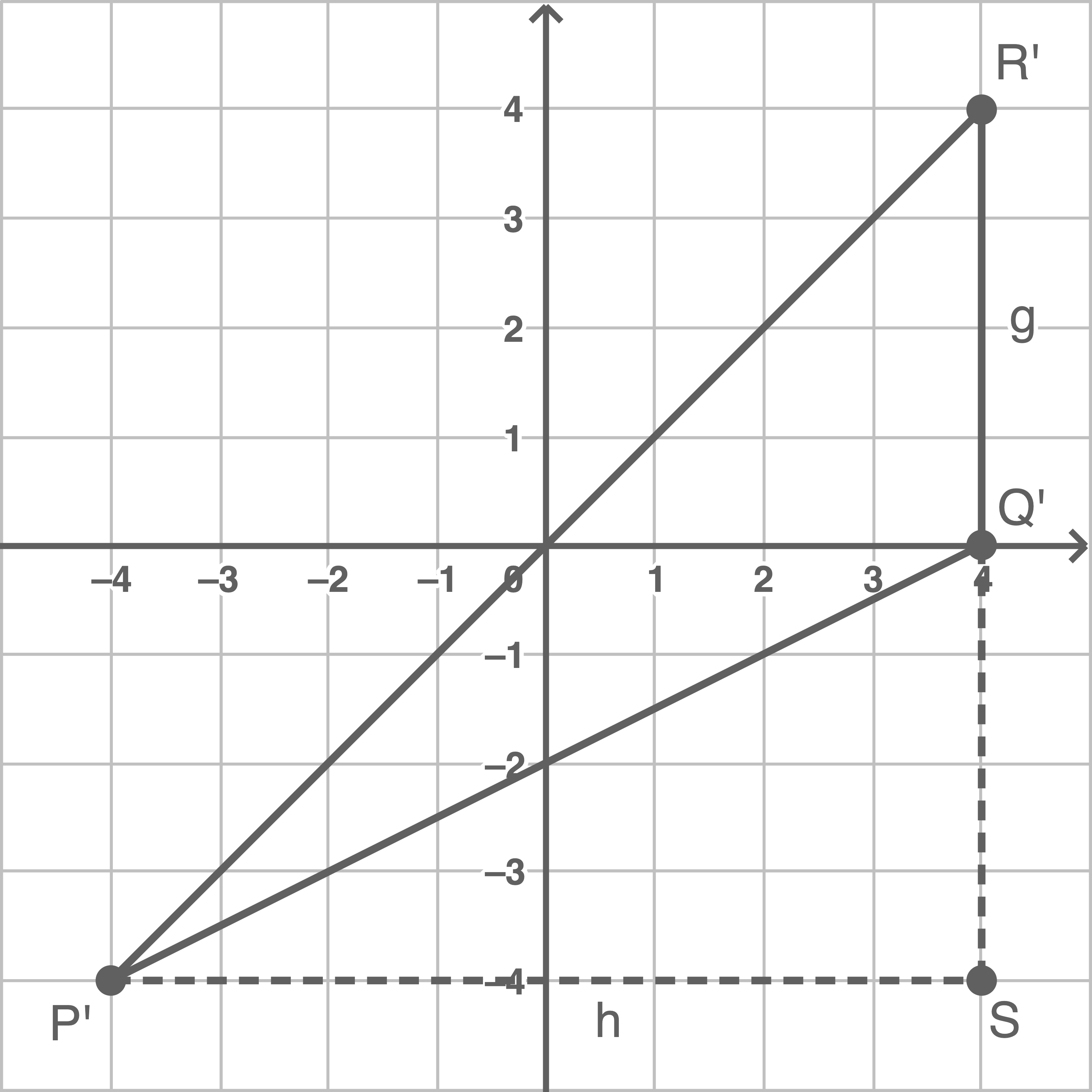
Flächeninhalt von 
berechnen
Die Länge der Seiten können mithilfe der Skizze bestimmt werden.
![\(\begin{array}[t]{rll}
A&=& \dfrac{1}{2}\cdot g \cdot h \\[5pt]
&=& \dfrac{1}{2}\cdot 4 \cdot 8 \\[5pt]
&=& 16
\end{array}\)](https://mathjax.schullv.de/7e4308ac00b3e5ab43faa243915edb6d3febd4aae1eea2f85ad95a7d1ec4a769?color=5a5a5a)
Das Dreieck hat einen Flächeninhalt von 16 FE.
Flächeninhalt von
3.
a)
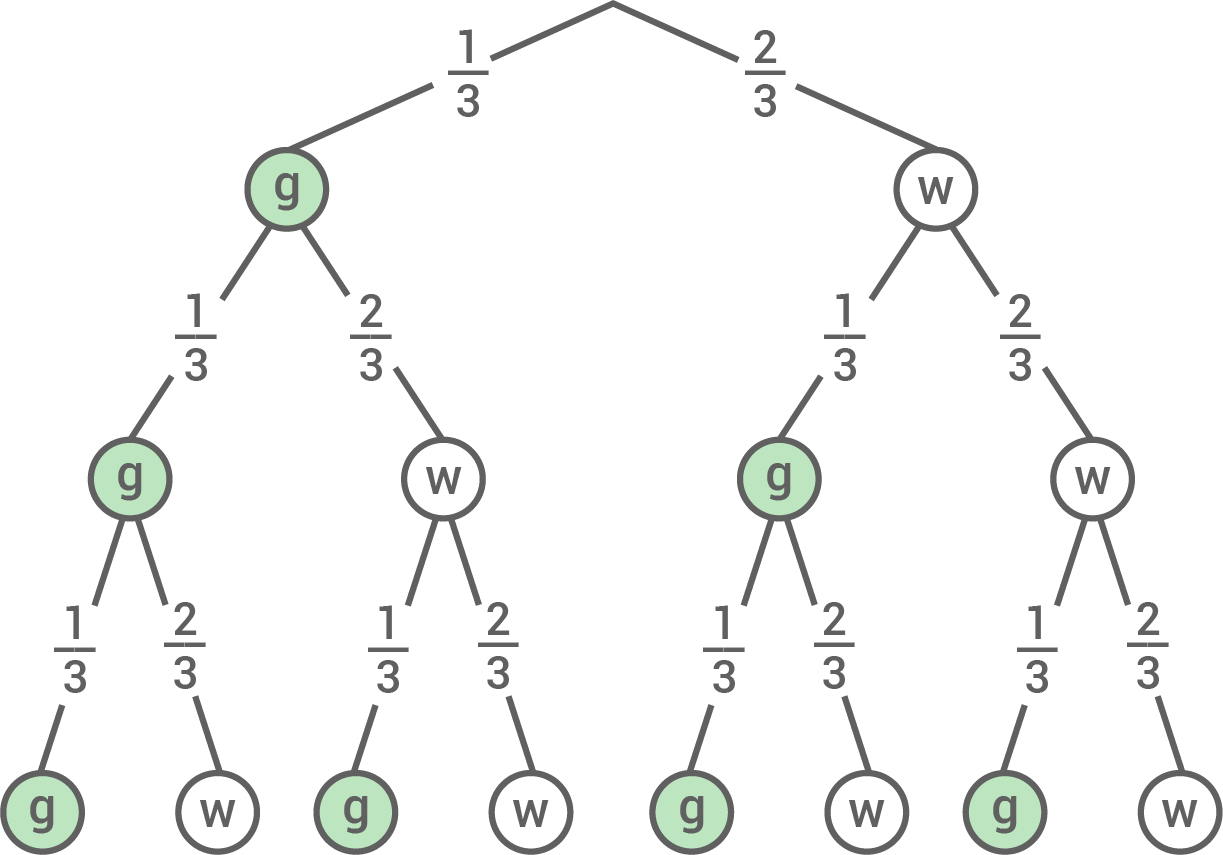
b)
Bei einem Einsatz von 1 € muss wieder 1 € gewonnen werden, damit bei dem Spiel weder Geld verloren noch gewonnen wird. Das ist der Fall, wenn genau einmal „grün“ gedreht wird.
![\(\begin{array}[t]{rll}
P(\text{gww, wgw, wwg})&=& 3\cdot \dfrac{1}{3}\cdot \left(\dfrac{2}{3}\right)^2 \\[5pt]
&=& \dfrac{4}{9}
\end{array}\)](https://mathjax.schullv.de/ffdb704c7bf6c786e7e7c2c3751bd199344aae1e17f29159ddb3c02a493fc08a?color=5a5a5a)
c)
Eine Aussage darüber, ob auf lange Sicht ein Gewinn zu erwarten ist, macht der Erwartungswert.
Zuerst müssen die Wahrscheinlichkeiten der verschiedenen Ereignisse berechnet werden:
„Es wird kein grün gedreht.“
In diesem Fall verliert der Spieler 1 €.
„Es wird einmal grün gedreht.“
In diesem Fall beträgt der Gewinn 0 €.
„Es wird zweimal grün gedreht.“
In diesem Fall gewinnt der Spieler 1 €.
„Es wird dreimal grün gedreht.“
In diesem Fall gewinnt der Spieler 5 €. Der Erwartungswert lässt sich als die Summe der Produkte der Gewinne mit der jeweiligen Wahrscheinlichkeit berechnen. Es ist pro Spiel mit einem Gewinn von
zu rechnen.
In diesem Fall verliert der Spieler 1 €.
In diesem Fall beträgt der Gewinn 0 €.
In diesem Fall gewinnt der Spieler 1 €.
In diesem Fall gewinnt der Spieler 5 €. Der Erwartungswert lässt sich als die Summe der Produkte der Gewinne mit der jeweiligen Wahrscheinlichkeit berechnen. Es ist pro Spiel mit einem Gewinn von