Pflichtaufgabe 2 – Mit Hilfsmitteln
1.
Gegeben ist ein Dreieck  mit
mit 
 und
und 
a)
Berechne den Flächeninhalt des Dreiecks 
(2 BE)
b)
Berechne die Größe des Winkels 
(2 BE)
c)
Gegeben ist die Funktion  mit
mit  Begründe, dass der Graph von
Begründe, dass der Graph von  parallel zur Seite
parallel zur Seite  verläuft.
verläuft.
(2 BE)
d)
Für jede reelle Zahl  ist eine Funktion
ist eine Funktion  gegeben durch
gegeben durch  Untersuche die Anzahl der gemeinsamen Punkte des Graphen von
Untersuche die Anzahl der gemeinsamen Punkte des Graphen von  mit den Seiten des Dreiecks
mit den Seiten des Dreiecks  in Abhängigkeit von
in Abhängigkeit von 
(4 BE)
2.
Anhand von Videoanalysen im Training wird die Wurftechnik von Basketballspielern erfasst und mathematisch beschrieben. Bei einem Trainingswurf wurden für den Spieler Hannes Werte erfasst (siehe Skizze). Der Ball verlässt die Hand von Hannes in einer Höhe von 
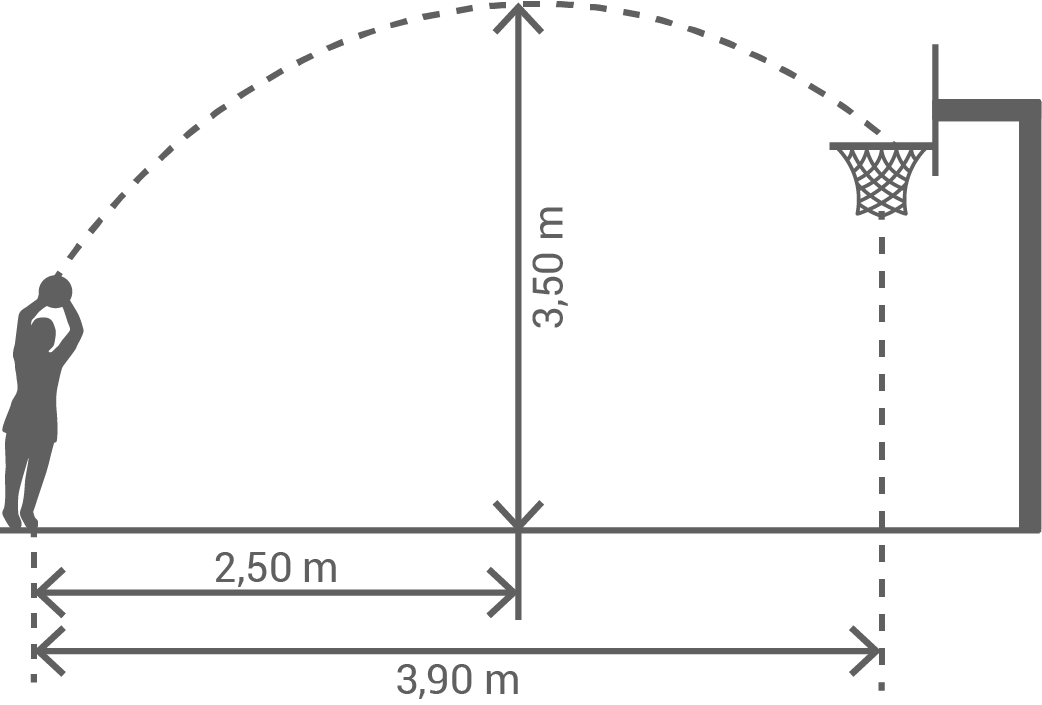 Die Flugbahn des Balles wird im Modell näherungsweise durch einen Teil des Graphen der Funktion
Die Flugbahn des Balles wird im Modell näherungsweise durch einen Teil des Graphen der Funktion  mit
mit  beschrieben.
beschrieben.
Der Ball wird in diesem Modell als Punkt aufgefasst.

Der Ball wird in diesem Modell als Punkt aufgefasst.
a)
Der Basketballkorb hängt in  Höhe.
Untersuche rechnerisch, ob der Ball den Korb trifft.
Höhe.
Untersuche rechnerisch, ob der Ball den Korb trifft.
(2 BE)
b)
Vor Hannes steht ein Abwehrspieler. Dieser erreicht mit nach oben gestreckten Armen eine Höhe von  Berechne den Mindestabstand, den der Abwehrspieler von Hannes haben muss, damit der Ball nicht abgewehrt wird.
Berechne den Mindestabstand, den der Abwehrspieler von Hannes haben muss, damit der Ball nicht abgewehrt wird.
(3 BE)
3.
Bei einer Verkehrskontrolle vor einer Schule wurde geprüft, ob bei den Fahrrädern Licht, Bremsen und Reifen in Ordnung sind. Die erfassten relativen Häufigkeiten werden dabei als Wahrscheinlichkeiten angenommen (siehe Baumdiagramm).
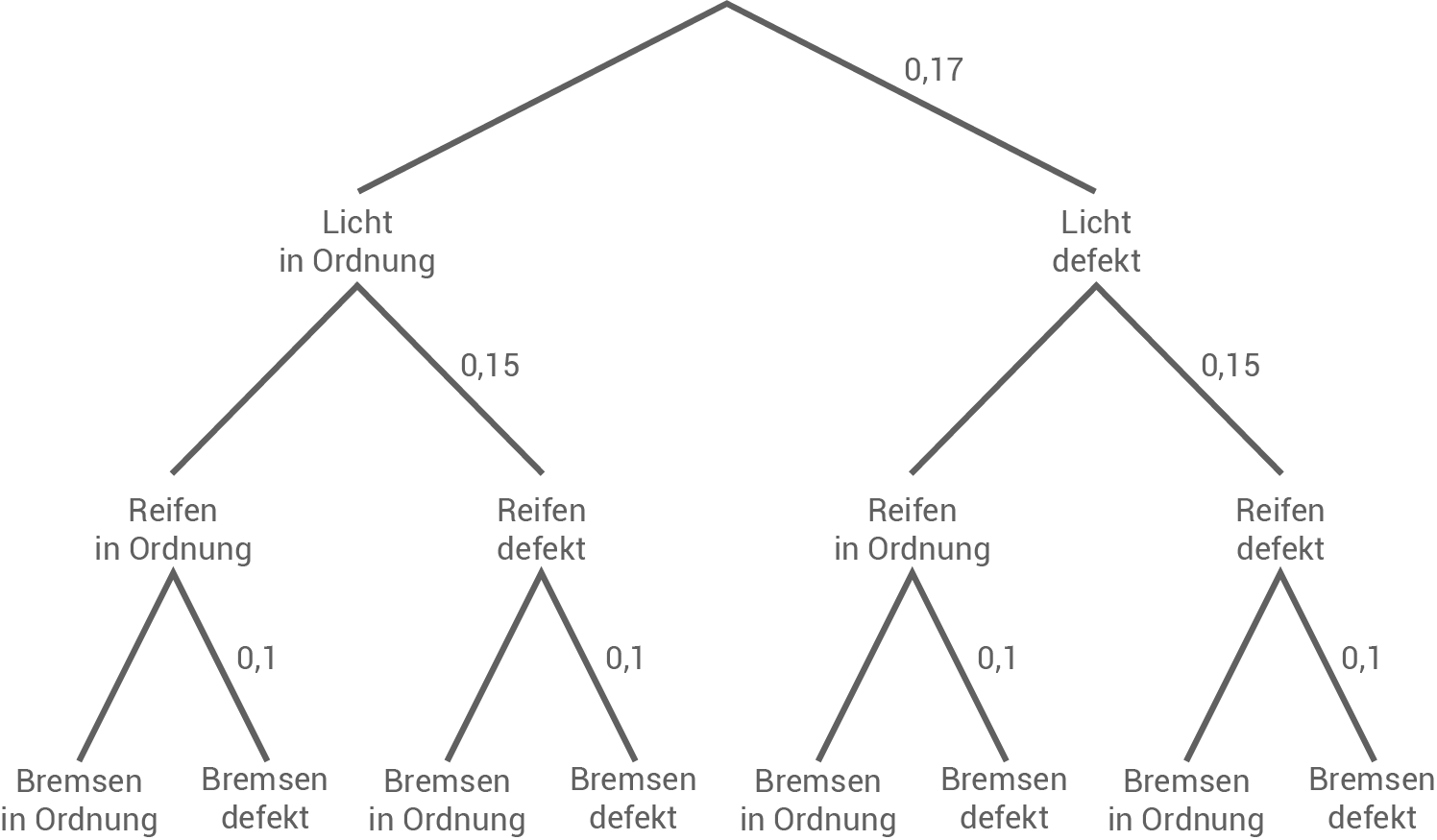

a)
Berechne die Wahrscheinlichkeit dafür, dass bei einem zufällig ausgewählten Fahrrad Licht, Bremsen und Reifen in Ordnung sind.
(2 BE)
b)
Beschreibe ein Ereignis  mit eigenen Worten, dessen Wahrscheinlichkeit sich mit dem folgenden Term berechnen lässt:
mit eigenen Worten, dessen Wahrscheinlichkeit sich mit dem folgenden Term berechnen lässt:
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
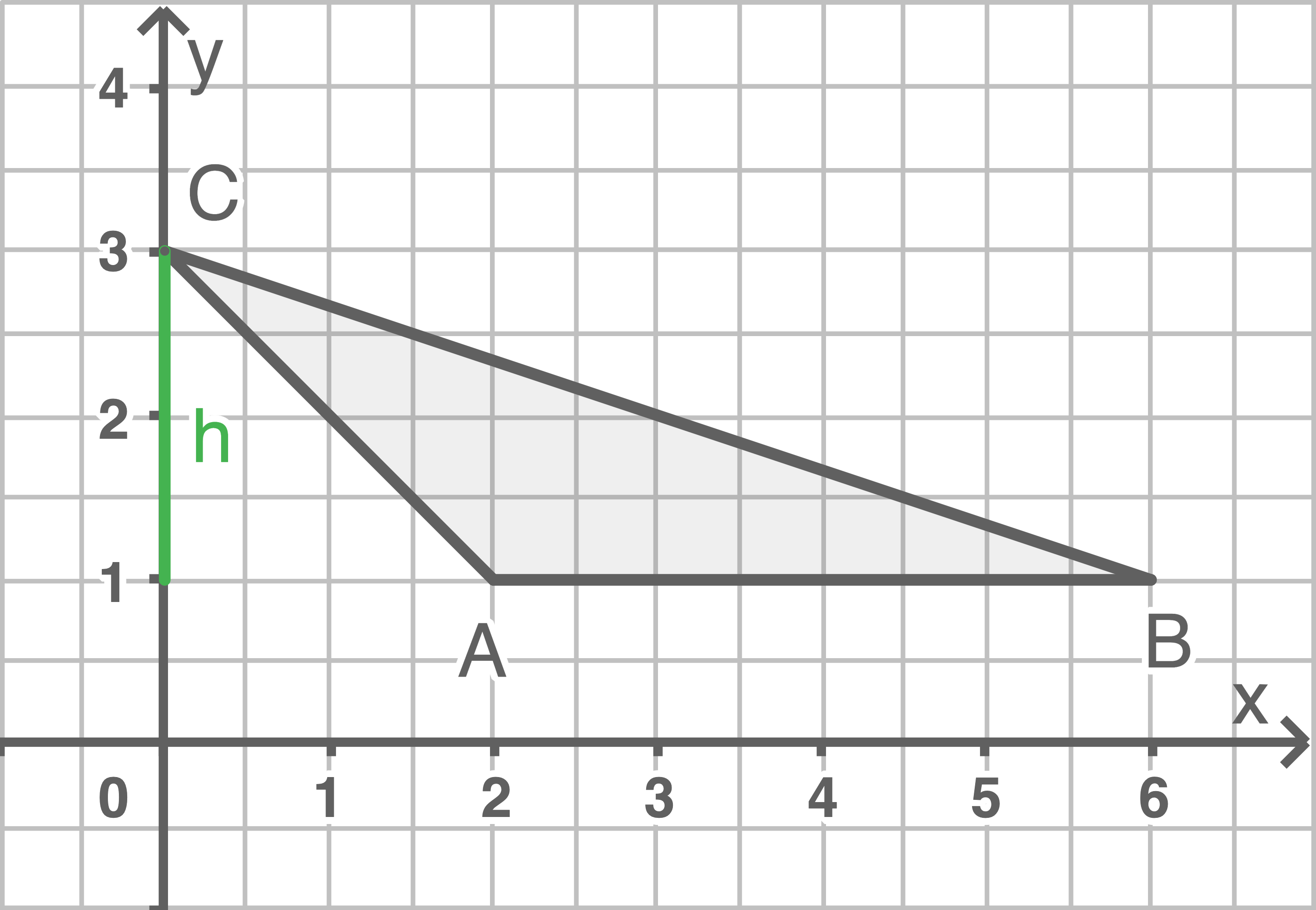
Skizze
b)
c)
Anstieg der Seite  berechnen:
berechnen:
 Der Anstieg stimmt mit dem der Funktion
Der Anstieg stimmt mit dem der Funktion  überein. Daher verlaufen der Graph von
überein. Daher verlaufen der Graph von  und die Seite
und die Seite  parallel.
parallel.
d)
Anstieg  berechnen, für den der Graph der Geraden
berechnen, für den der Graph der Geraden  durch den Punkt
durch den Punkt  verläuft:
verläuft:
 Für
Für  hat der Graph von
hat der Graph von  genau einen gemeinsamen Punkt mit den Seiten des Dreiecks
genau einen gemeinsamen Punkt mit den Seiten des Dreiecks  Anhand der Skizze in Teilaufgabe a) lässt sich insgesamt erkennen:
Anhand der Skizze in Teilaufgabe a) lässt sich insgesamt erkennen:
 keine gemeinsamen Punkte
keine gemeinsamen Punkte
 ein gemeinsamer Punkt
ein gemeinsamer Punkt
 zwei gemeinsame Punkte
zwei gemeinsame Punkte
2.
a)
b)
Der Abwehrspieler muss mindestens so weit entfernt sein wie die Stelle, an der  gilt. Der solve-Befehl des CAS liefert die Lösungen
gilt. Der solve-Befehl des CAS liefert die Lösungen  und
und  Damit lässt sich der Mindestabstand berechnen:
Damit lässt sich der Mindestabstand berechnen:
 Der Abstand muss mindestens
Der Abstand muss mindestens  betragen.
betragen.
3.
a)
b)