Wahlaufgabe 2

Aus einem pyramidenförmigen Holzstück mit quadratischer Grundfläche wurde ein Podest (siehe Skizze) hergestellt.

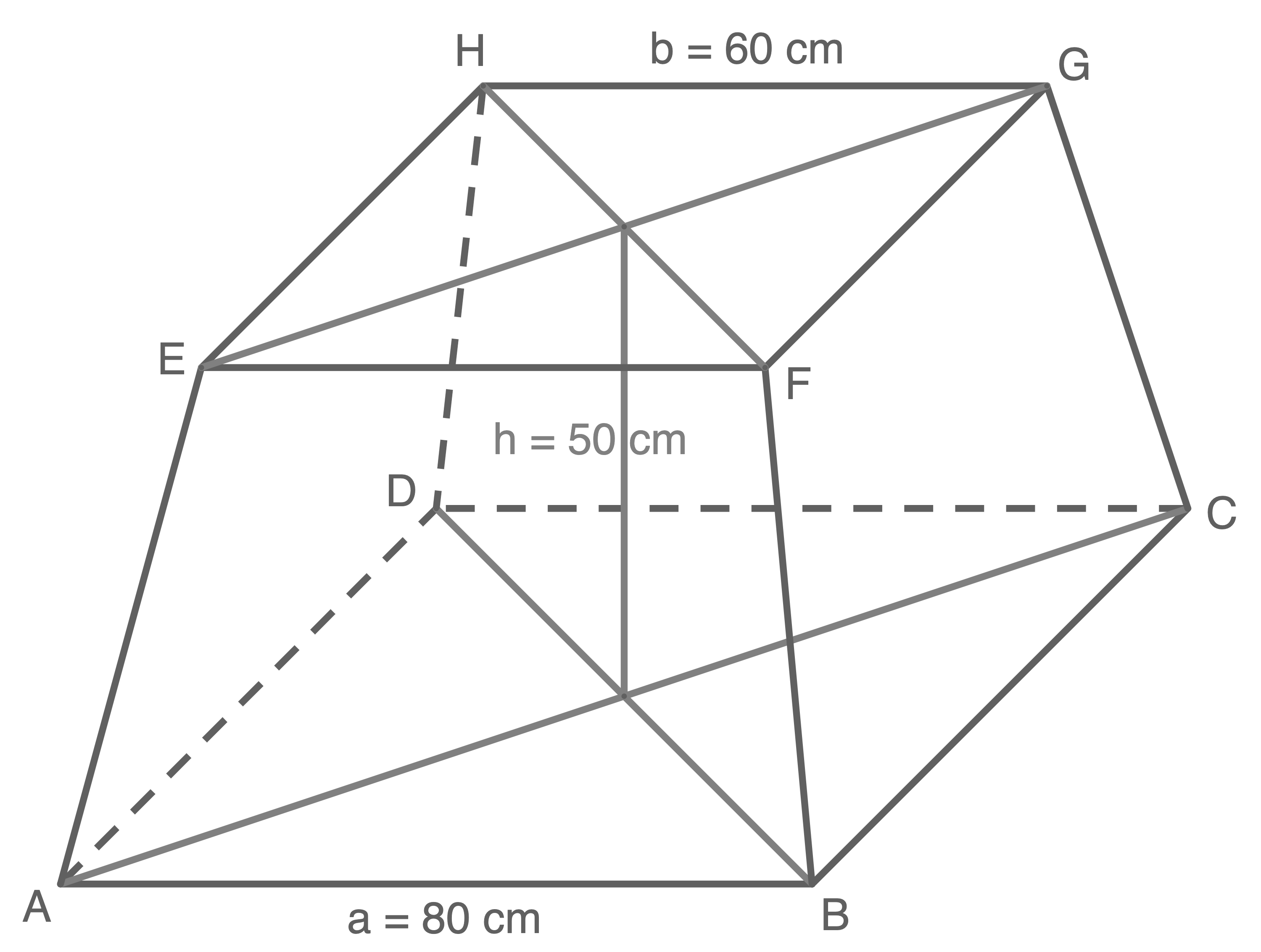
Skizze nicht maßstäblich

Zeichne den Grundriss des dargestellten Körpers in einem geeigneten Maßstab. Gib diesen Maßstab an.

(3 BE)

Berechne die ursprüngliche Höhe des Holzstücks.

(3 BE)

Zur Berechnung der Flächeninhalts einer Seitenfläche des Podests notiert Lisa die Formel:
$A=\dfrac{1}{2}\cdot\left(a+b\right)\cdot h$
Entscheide, ob dieser Ansatz richtig ist. Begründe deine Entscheidung.

(2 BE)

Aus Walnüssen und Erdnüssen werden 200 kg einer Nussmischung hergestellt. Der Preis für Walnüsse beträgt 7,00 € pro Kilogramm, der für Erdnüsse 2,50 € pro Kilogramm.
Ermittle die Massen von Walnüssen und Erdnüssen, damit der Preis dieser Nussmischung 3,40 € pro Kilogramm beträgt.

(4 BE)

Ein Spielautomat besteht aus drei Glücksrädern mit jeweils gleich großen Sektoren. Die drei Glücksräder werden pro Spiel gleichzeitig in Bewegung gesetzt.

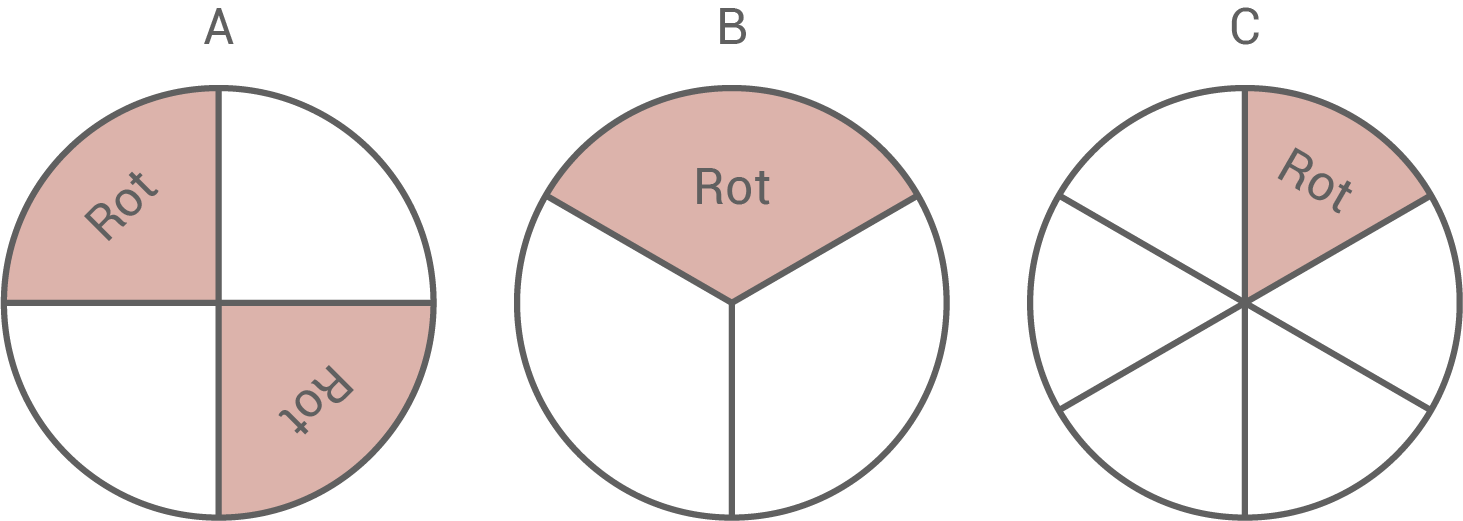
Regeln:
Der Einsatz pro Spiel beträgt drei Euro.
Zeigen alle drei Glücksräder Rot, werden 12 Euro ausgezahlt.
Zeigen zwei Glücksräder Rot, erhält man 6 Euro.
In allen anderen Fällen erhält man nichts.

Stelle den Sachverhalt in einem vollständig beschrifteten Baumdiagramm dar. Ermittle die Wahrscheinlichkeit dafür, dass der Spieler Geld gewinnt.

(4 BE)

Begründe, dass dieses Spiel nicht fair ist.
Verändere die Regeln so, dass es sich um ein faires Spiel handelt.

Hinweis: Ein Spiel heißt fair, wenn der Erwartungswert des Gewinns Null ist.

(4 BE)

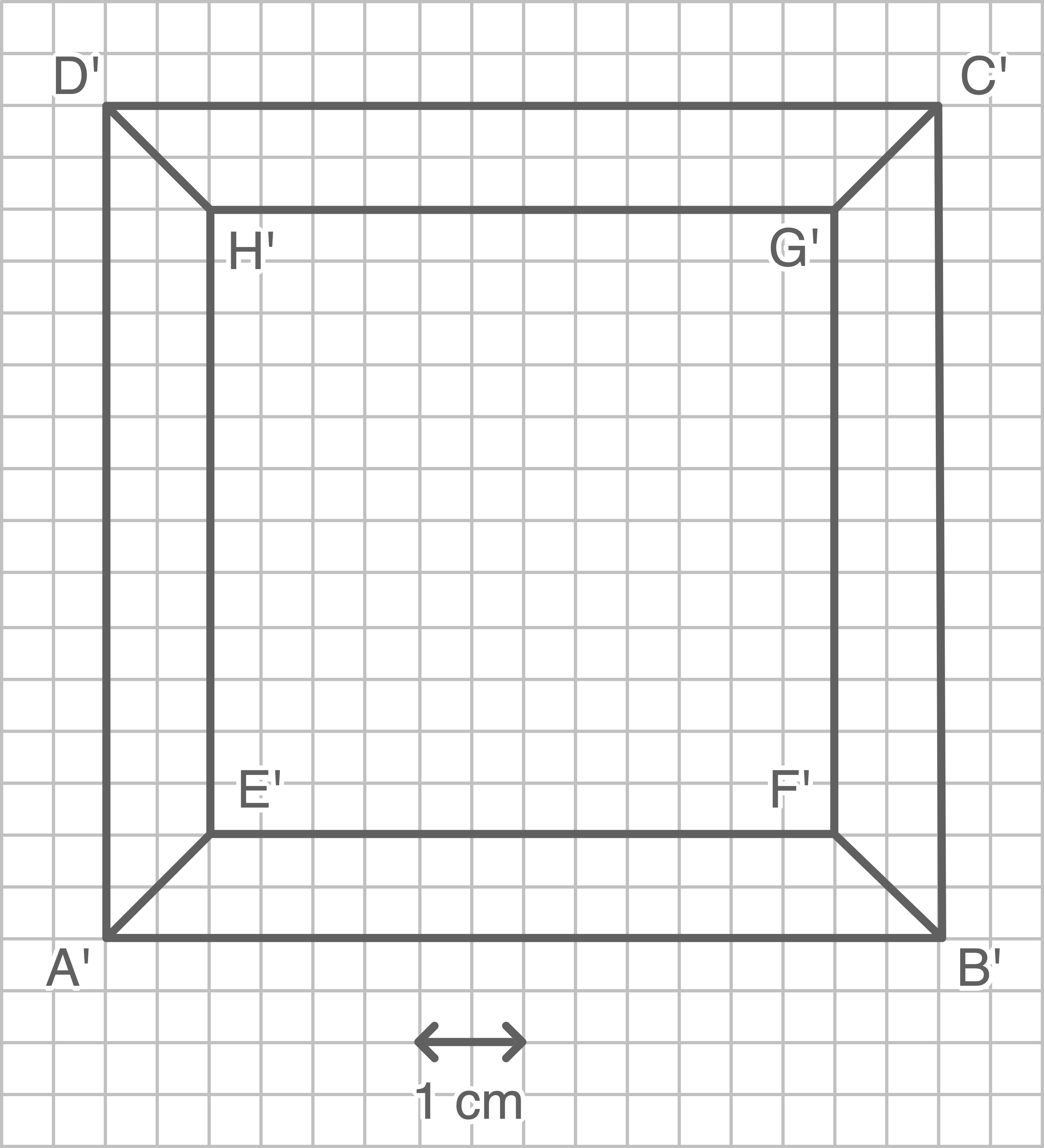
Grundriss im Maßstab 1:10

Die Höhe $\overline{MS}$ kann mithilfe des Strahlensatzes berechnet werden.

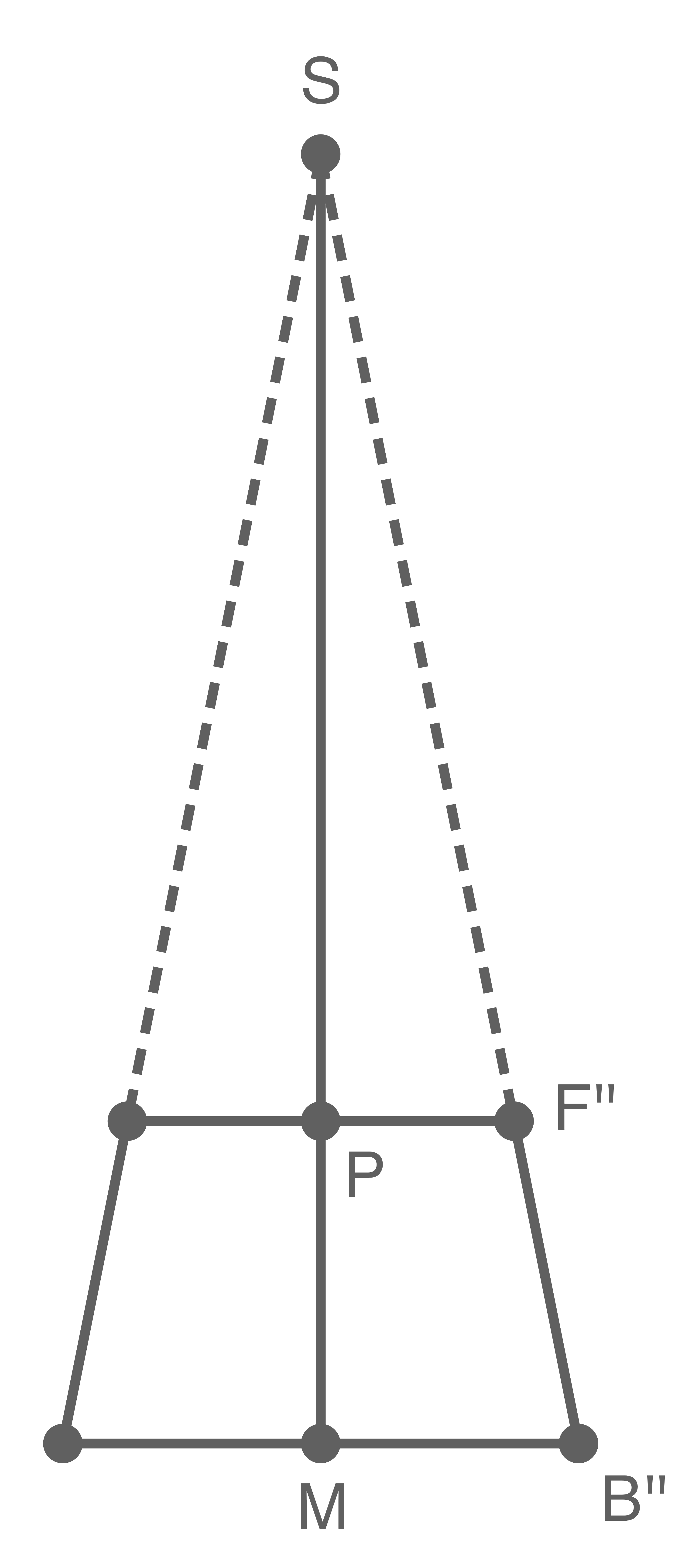Dazu wird zunächst die Höhe $\overline{PS}$ berechnet:

$\(\begin{array}[t]{rll} \dfrac{\overline{PS}}{\overline{PF$

Mit dem Taschenrechner folgt $\overline{PS}=150.$ Damit folgt für die Gesamthöhe des Holzstücks:

$\overline{MS}=\overline{MP}+\overline{PS}=50+150=200$

Die ursprüngliche Höhe des Holzstücks betrug 200 cm.

Lisas Ansatz ist falsch.

Die Körperhöhe entspricht nicht der Trapezhöhe der Seitenflächen.

$x:$ Masse der Walnüsse in kg
$y:$ Masse der Erdnüsse in kg

Mit den gegebenen Informationen lässt sich das folgende Gleichungssystem aufstellen:

$\begin{array}{lrll} \text{I}\quad& x&+& &y& =& 200 &\\ \text{II}\quad& 7x&+& 2,5&y&=& 200\cdot 3,4 & \end{array}$

Der Taschenrechner liefert $x=40$ und $y=160.$

Für die Mischung werden 40 kg Walnüsse und 160 kg Erdnüsse verwendet.

Sachverhalt in Baumdiagramm darstellen

$r:$ Ein Glücksrad zeigt Rot an
$w:$ Ein Glücksrad zeigt nicht Rot an

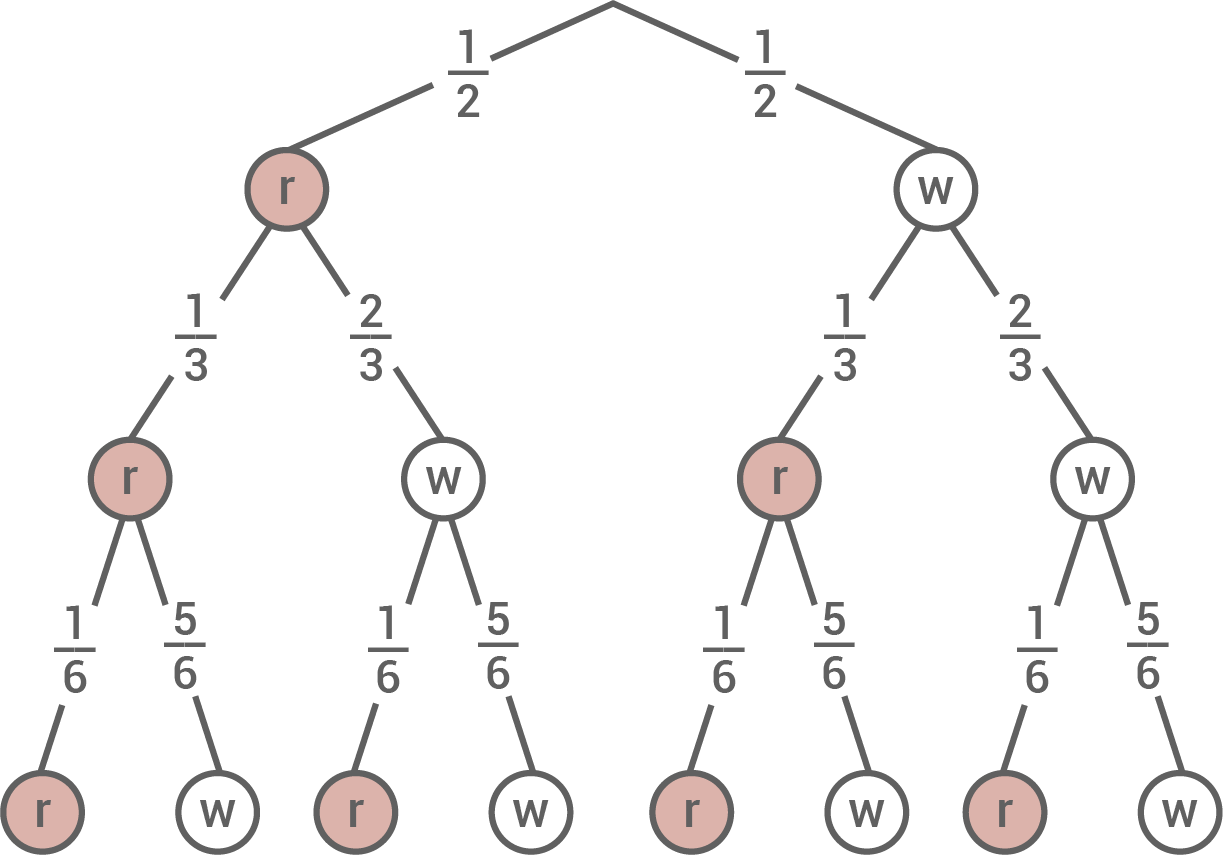Wahrscheinlichkeit für Gewinn ermitteln

Der Spieler gewinnt Geld, wenn mindestens zweimal Rot angezeigt wird:

Rechenweg anzeigen

$p=\dfrac{1}{4}$

Begründen, dass Spiel nicht fair ist

$P(\text{„dreimal Rot“})=\dfrac{1}{2}\cdot \dfrac{1}{3}\cdot \dfrac{1}{6}=\dfrac{1}{36}$

Der Gewinn beträgt in diesem Fall 9 €.

Rechenweg anzeigen

$P(\text{„zweimal Rot“})=\dfrac{8}{36}$

Der Gewinn beträgt in diesem Fall 3 €.

Rechenweg anzeigen

$P(\text{„höchstens einmal Rot“})=\dfrac{27}{36}$

Der Verlust beträgt in diesem Fall 3 €.

Rechenweg anzeigen

$E(X)=-1,33\,€$

Es gilt also $E(X)\neq 0$ , daher ist das Spiel nicht fair.

Regeln verändern, sodass Spiel fair ist

Es gibt verschiedene Möglichkeiten, das Spiel so zu verändern, dass es fair ist. Eine Möglichkeit ist, dass man nur noch bei dreimal Rot etwas gewinnt. Die Lösung der folgenden Gleichung liefert dann den in diesem Fall ausgezahlten Wert:

$(x-3) \cdot \dfrac{1}{36}+(0-3) \cdot \dfrac{8}{36}+(0-3) \cdot \dfrac{27}{36}=0$

Der Taschenrechner liefert $x=108.$

Das Spiel ist fair, wenn der Spieler bei $3\,€$ Einsatz nur bei dreimal Rot $108\,€$ ausgezahlt bekommt und sonst nichts.