Pflichtaufgabe 1 – Ohne Hilfsmittel
1.
Gegeben sind die Funktionen 
und 
durch:
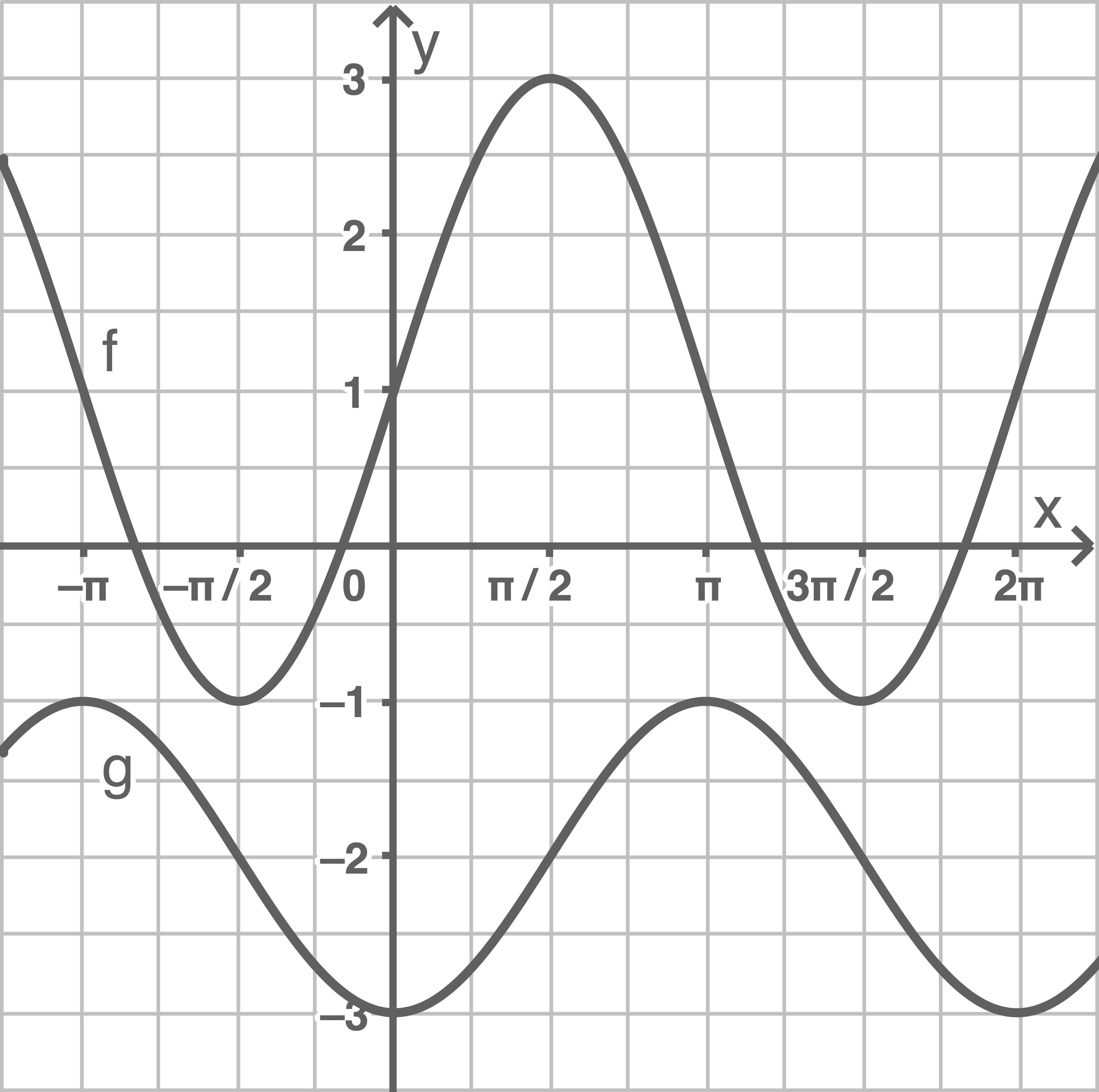
Skizziere die Graphen von und im Intervall 
(2 BE)
2.
Berechne die Schnittstelle der Graphen der linearen Funktionen und 
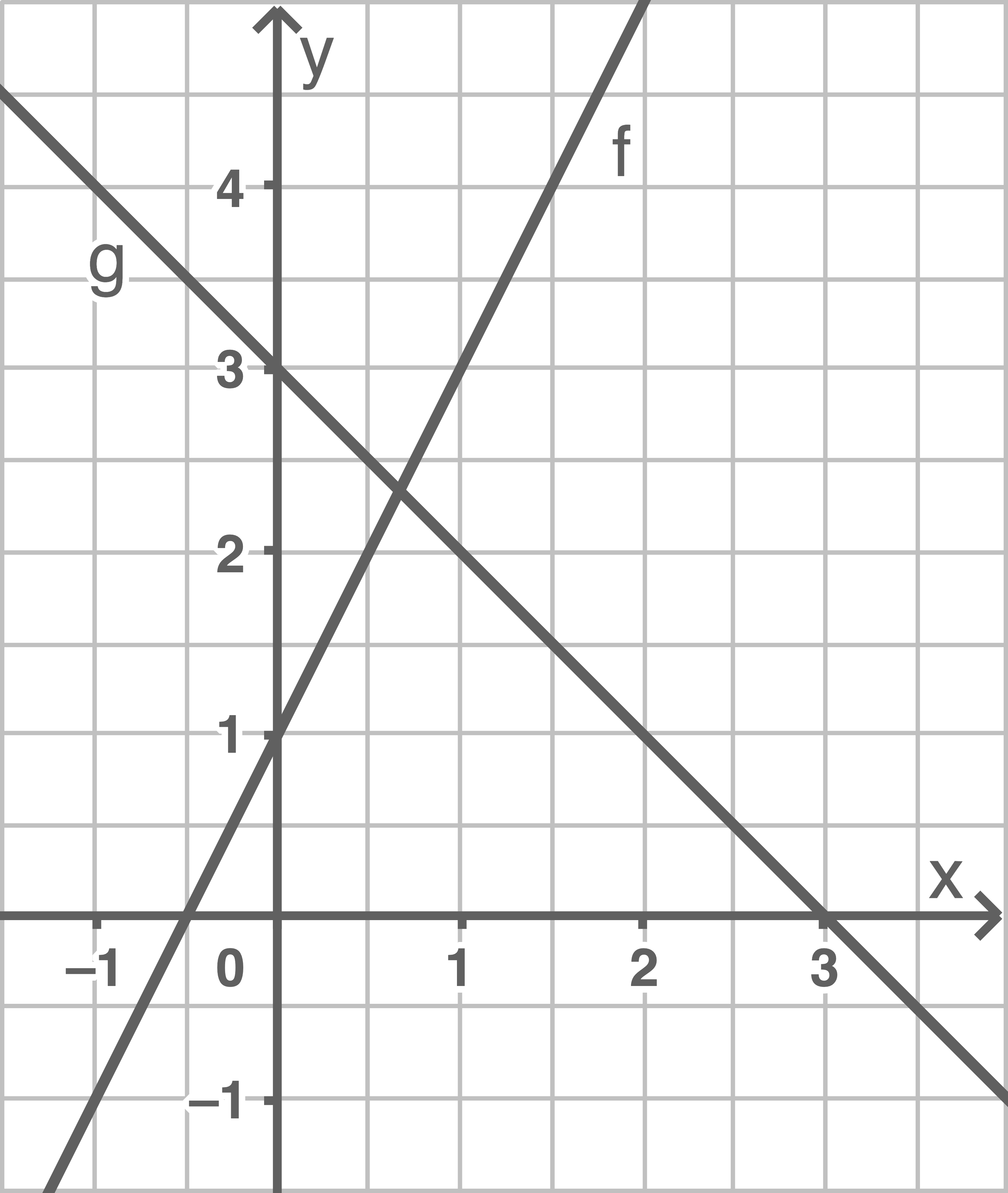
(3 BE)
3.
Für jede reelle Zahl 
ist eine Funktion mit 
gegeben.
Bestimme die reelle Zahl so, dass sich die Graphen der Funktionen und mit 
an der Stelle 
schneiden.
(1 BE)
4.
Gegeben ist ein rechtwinkliges Dreieck 
Gib vollständige Gleichungen unter Verwendung der Dreiecksseiten an.![\(\begin{array}[t]{rll}
\sin(\alpha)&=& \\
\tan(\beta)&=&
\end{array}\)](https://mathjax.schullv.de/6128cf6a01db2953b62fe64ec99259c10f6fd8664e6d8bfcf3fabd21f4da8df7?color=5a5a5a)
Gib vollständige Gleichungen unter Verwendung der Dreiecksseiten an.
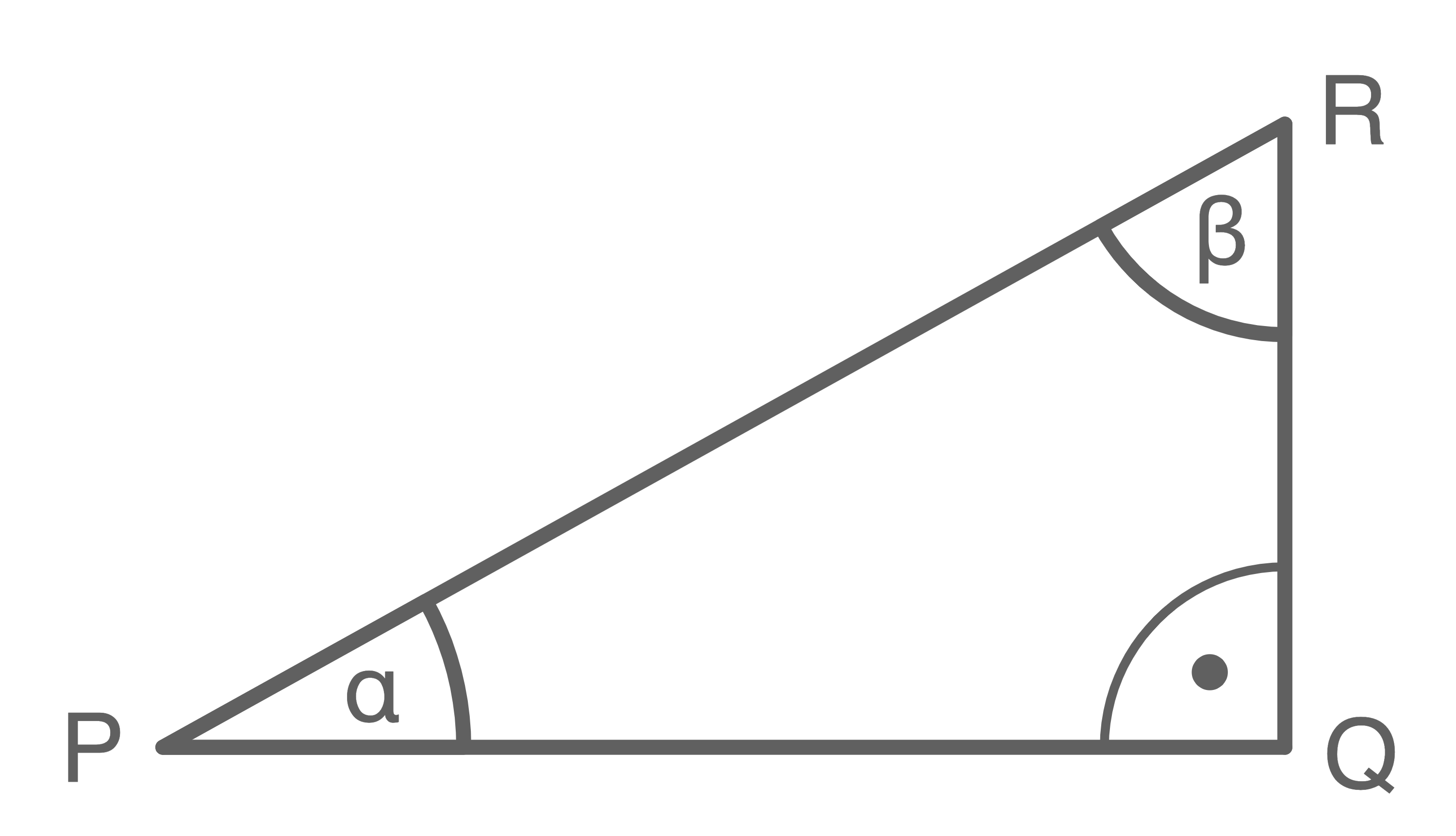
(3 BE)
5.
Für ein Spiel soll das abgebildete Glücksrad verwendet werden.
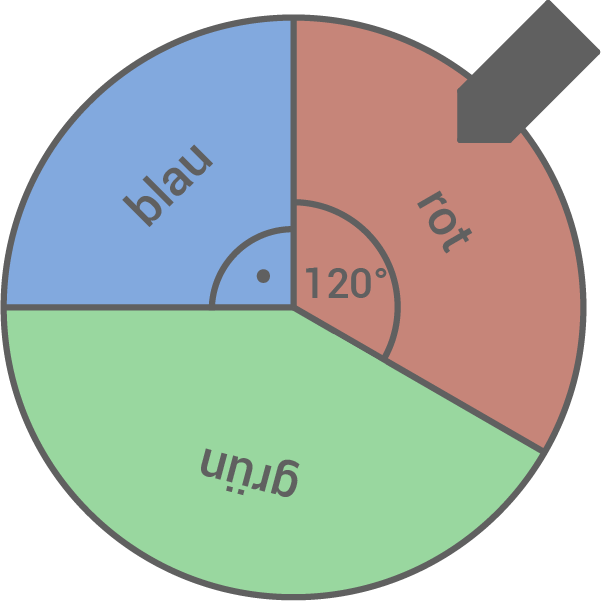
Laura schlägt ihrer Freundin vor, anstelle des Glücksrads ein Ziehungsgefäß mit blauen, roten und grünen Kugeln zu verwenden. Die Wahrscheinlichkeiten für die Ereignisse „rot“, „blau“ und „grün“ sollen gegenüber dem Glücksrad unverändert bleiben.
Zur Auswahl sind fünf rote, fünf blaue und fünf grüne Kugeln vorhanden.
Erläutere, dass damit das Spiel unter den geforderten Bedingungen durchgeführt werden kann.
Laura schlägt ihrer Freundin vor, anstelle des Glücksrads ein Ziehungsgefäß mit blauen, roten und grünen Kugeln zu verwenden. Die Wahrscheinlichkeiten für die Ereignisse „rot“, „blau“ und „grün“ sollen gegenüber dem Glücksrad unverändert bleiben.
Zur Auswahl sind fünf rote, fünf blaue und fünf grüne Kugeln vorhanden.
Erläutere, dass damit das Spiel unter den geforderten Bedingungen durchgeführt werden kann.
(2 BE)
1.
Der Graph von wird entlang der 
-Achse um den Faktor 2 gestreckt und durch den Summanden 1 um eine Einheit entlang der -Achse nach oben verschoben.
Durch den Faktor -1 wird der Graph von an der 
-Achse gespiegelt und durch den Summanden -2 entlang der -Ache um zwei Einheiten nach unten verschoben.
2.
Funktionsgleichungen aufstellen
bestimmt werden.
Schnittstelle berechnen
Die Schnittstelle wird durch Gleichsetzen der beiden Funktionen bestimmt.
![\(\begin{array}[t]{rll}
f(x)&=& g(x) \\[5pt]
2x+1&=& -x+3 &\quad \scriptsize \mid\;-1 \\[5pt]
2x&=& -x+2 &\quad \scriptsize \mid\;+x \\[5pt]
3x&=& 2 &\quad \scriptsize \mid\;:3 \\[5pt]
x&=& \dfrac{2}{3}
\end{array}\)](https://mathjax.schullv.de/194680d495483f03962d9660f8063a264481011a2d11a46e2bd62c612b84accc?color=5a5a5a)
Die Graphen der beiden linearen Funktionen und schneiden sich an der Stelle 
Die Steigung 
kann wie in der Skizze mithilfe von Steigungsdreiecken bestimmt werden. Der -Achsenabschnitt 
kann direkt abgelesen werden. Diese Werte werden dann in die allgemeine Funktionsgleichung 
eingesetzt.
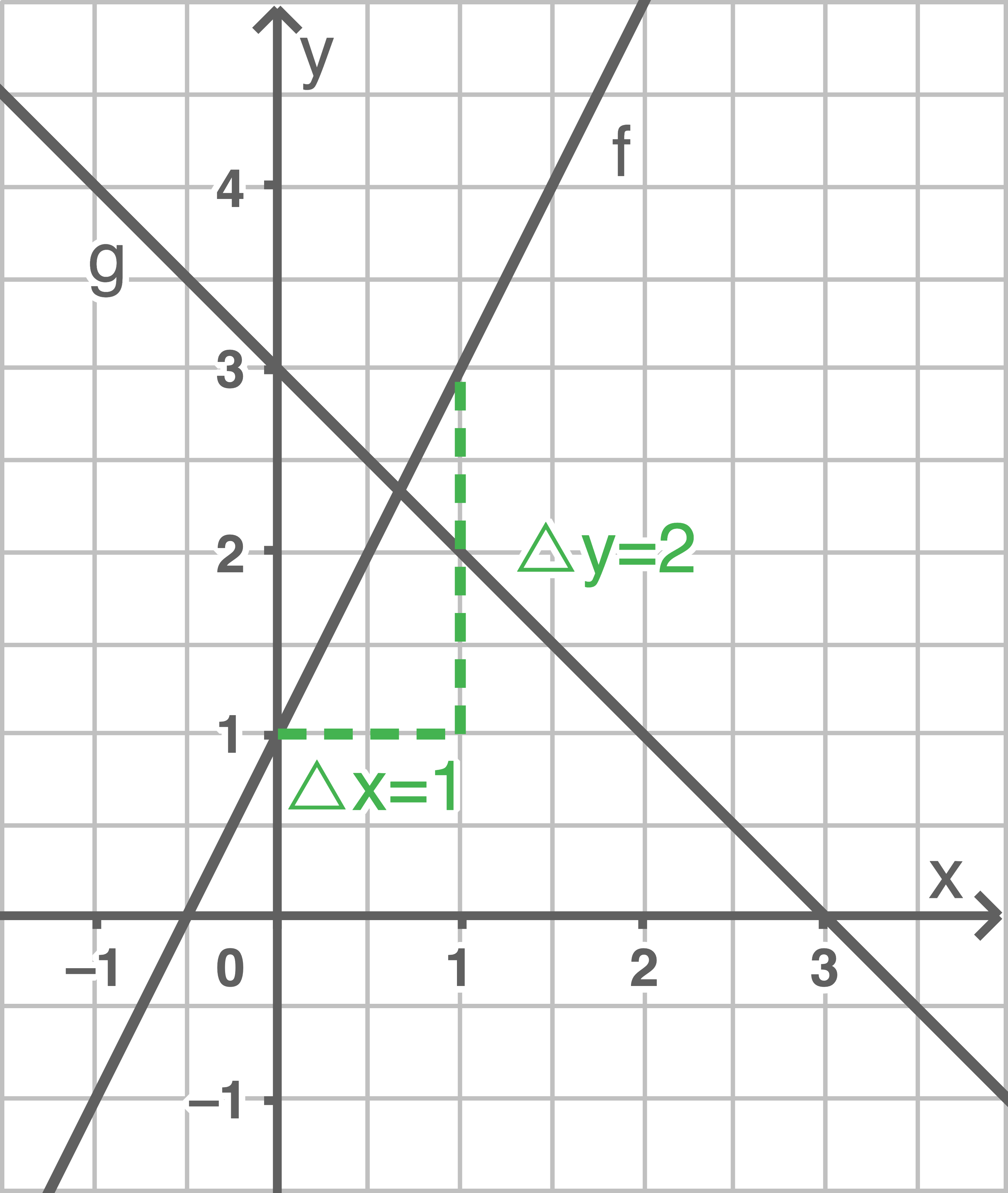Für die Funktionsgleichung von gilt:
Der -Achsenabschnitt beträgt 
Insgesamt folgt 
Analog kann die Funktionsgleichung
3.
Wenn sich die beiden Funktionen an der Stelle schneiden sollen, muss 
gelten.
![\(\begin{array}[t]{rll}
f(1)&=& g(1)\\[5pt]
-1^4+c&=& 3\cdot 1^4 \\[5pt]
-1+c&=& 3 &\quad \scriptsize \mid\; +1\\[5pt]
c&=& 4
\end{array}\)](https://mathjax.schullv.de/fb38728709370e34ae9ea491b43cffcadd4c93375619e05a7e49dd46f87710a6?color=5a5a5a)
Mit dem Wert 
schneiden sich die Graphen der beiden Funktionen und an der Stelle 
4.
5.
Die Wahrscheinlichkeiten der einzelnen Farben entsprechen dem jeweiligen Anteil des Sektors am gesamten Glücksrad:
Damit das gilt, müssen insgesamt zwölf Kugeln in das Ziehungsgefäß, davon 3 blaue, 4 rote und 5 grüne.