Wahlaufgabe 1
Eine Stadt plant den Bau eines neuen Spielplatzes.
a)
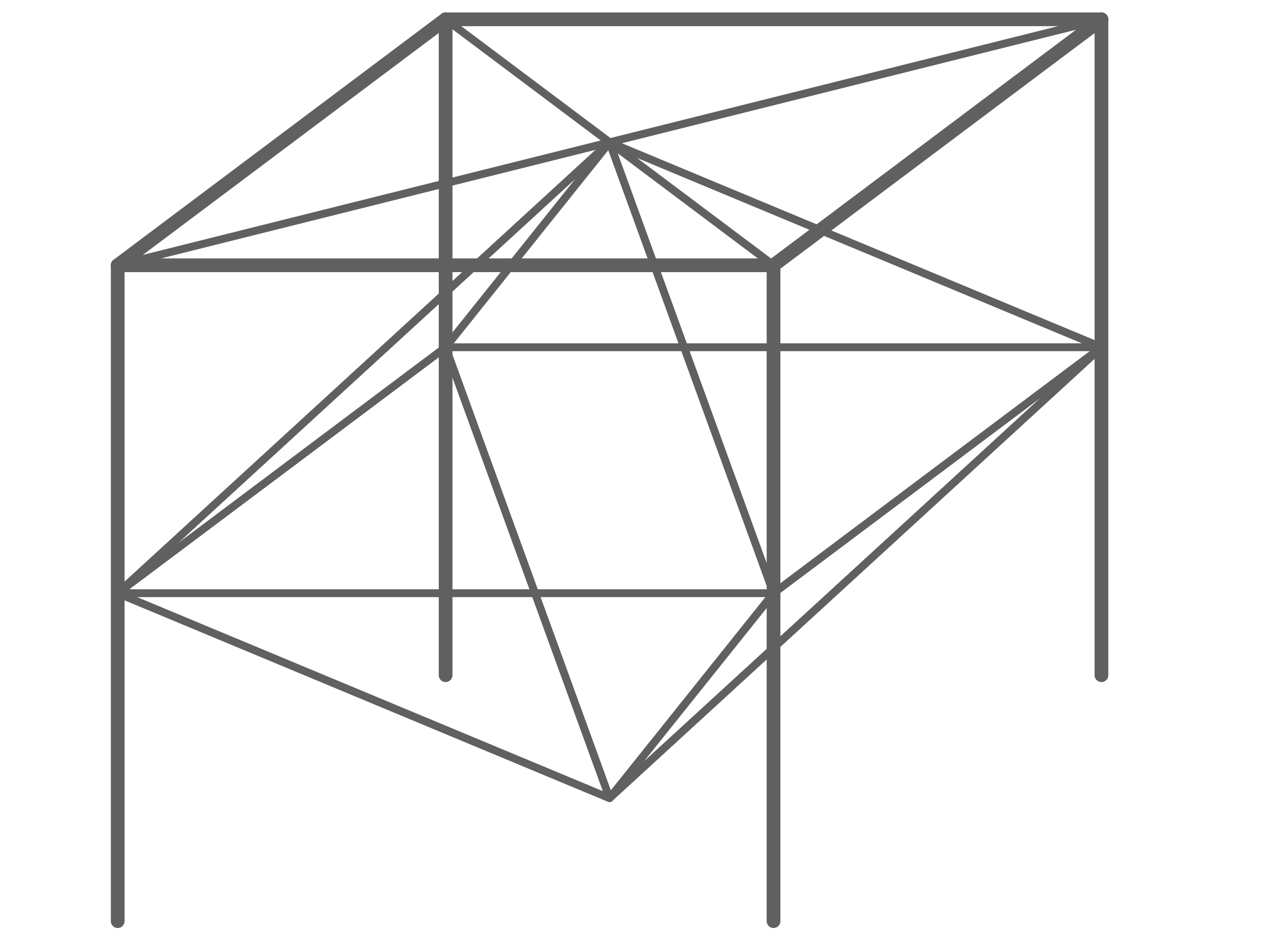
Das Klettergerüst soll die Form eines Würfels mit einbeschriebener Doppelpyramide haben. Die Doppelpyramide besteht dabei aus zwei kongruenten, geraden Pyramiden mit gemeinsamer Grundfläche. Die Kantenlänge des Würfels beträgt 2 m. Dargestellt sind alle Metallrohre dieses geplanten Klettergerüsts.
Berechne die gesamte Länge der benötigten Metallrohre.
Berechne die gesamte Länge der benötigten Metallrohre.

Skizze nicht maßstäblich
(4 BE)
b)
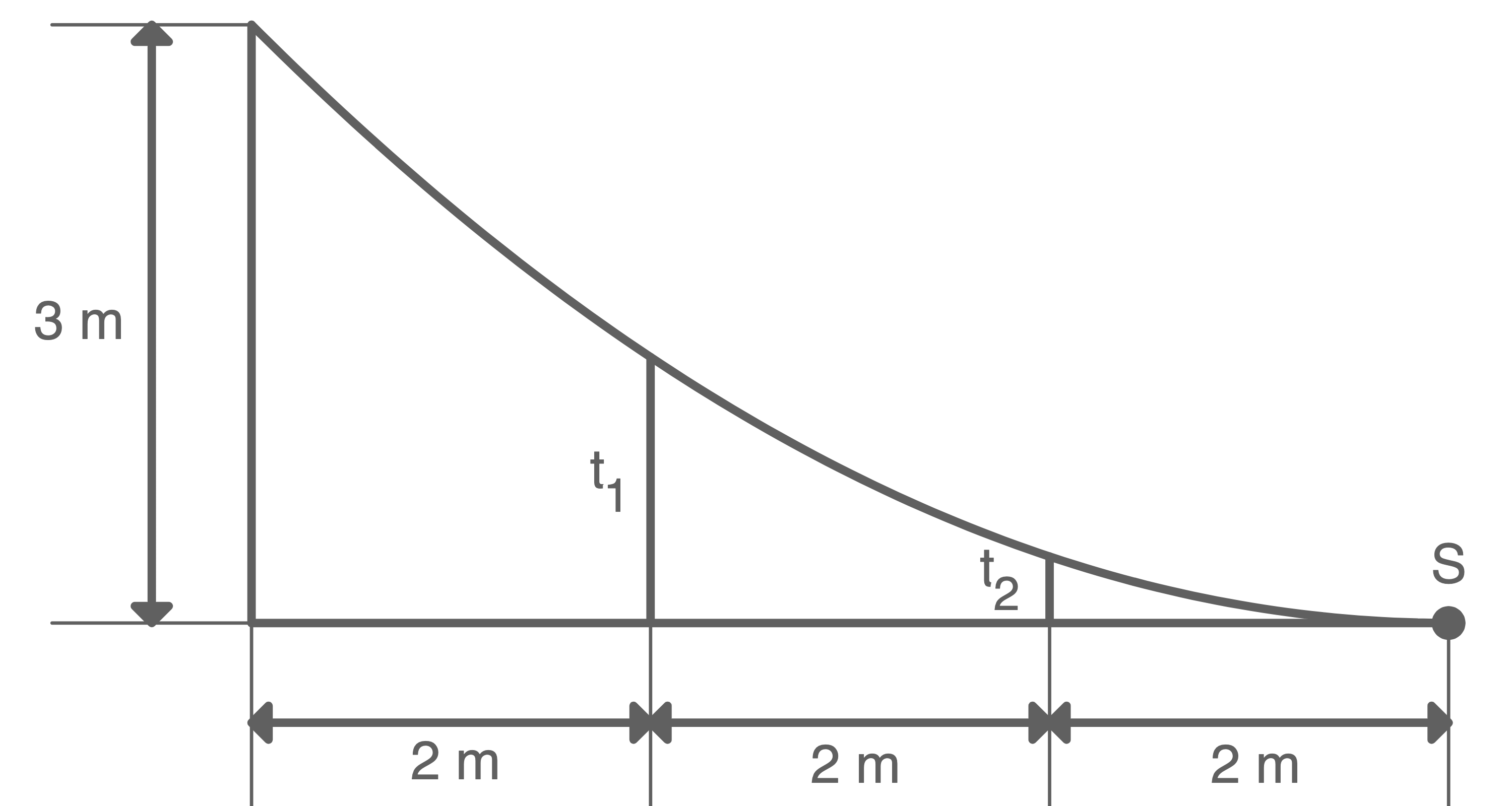
Die Darstellung zeigt einen Teil der Skateranlage im Profil.
Die Profillinie der befahrbaren Fläche hat näherungsweise die Form einer Parabel mit dem Scheitelpunkt
Berechne die Längen der beiden Träger und
und 
Die Profillinie der befahrbaren Fläche hat näherungsweise die Form einer Parabel mit dem Scheitelpunkt
Berechne die Längen der beiden Träger

Skizze nicht maßstäblich
(4 BE)
c)
Die Kosten für den Spielplatz betrugen nicht wie geplant 360 000 €, sondern 450 000 €.
Dazu wurde in der Presse veröffentlich:
Formuliere eine andere mathematisch korrekte Aussage zum oben genannten Sachverhalt.
Zur Eröffnung des Spielplatzes werden 2 500 Lose verkauft. Unter diesen Losen sind ein Hauptgewinn zu 500 €, fünf Gewinne zu 100 €, 100 Gewinne zu 5 € und 500 Kleingewinne im Wert von 2 €. Die anderen Lose sind Nieten.
Dazu wurde in der Presse veröffentlich:
- Die tatsächlichen Kosten sind im Vergleich zu den geplanten Kosten auf 125 % gestiegen.
- Für den Bau des Spielplatzes waren nur 80 % der tatsächlichen Kosten eingeplant.
Formuliere eine andere mathematisch korrekte Aussage zum oben genannten Sachverhalt.
(3 BE)
d)
Berechne die Wahrscheinlichkeiten folgender Ereignisse:


„Das erste verkaufte Los enthält den Hauptgewinn.“
„Mindestens eines der ersten drei verkauften Lose ist ein Gewinnlos.“
(2 BE)
e)
Nach Verkauf aller Lose und Auszahlung der Gewinne sollen 2 500 € übrig bleiben.
Ermittle den Preis für ein Los.
Ermittle den Preis für ein Los.
(2 BE)
a)
b)
Funktionsgleichung aufstellen
Als Scheitelpunkt bietet sich der Koordinatenursprung eines rechtwinkligen Koordinatensystems an. In diesem Fall kann die Parabel durch eine Funktionsgleichung der Form  beschrieben werden. Zudem kann aus der Skizze der Punkt
beschrieben werden. Zudem kann aus der Skizze der Punkt  abgeleitet werden.
Einsetzten dieser Koordinaten in die allgemeine Funktionsgleichung liefert:
abgeleitet werden.
Einsetzten dieser Koordinaten in die allgemeine Funktionsgleichung liefert:
![\(\begin{array}[t]{rll}
y &=& a\cdot x^2 \\[5pt]
3&=& a\cdot (-6)^2 \\[5pt]
3&=& a\cdot 36 \quad \scriptsize \mid\; :36 \\[5pt]
\dfrac{1}{12}&=& a
\end{array}\)](https://www.schullv.de/resources/formulas/f5fa8388f380d5b237b93be31c32b654e50c2a84df400229a3ab168bf9387f96_light.svg) Eine Gleichung der Parabel, die das Profil der Skateranlage beschreibt, lautet also:
Eine Gleichung der Parabel, die das Profil der Skateranlage beschreibt, lautet also:
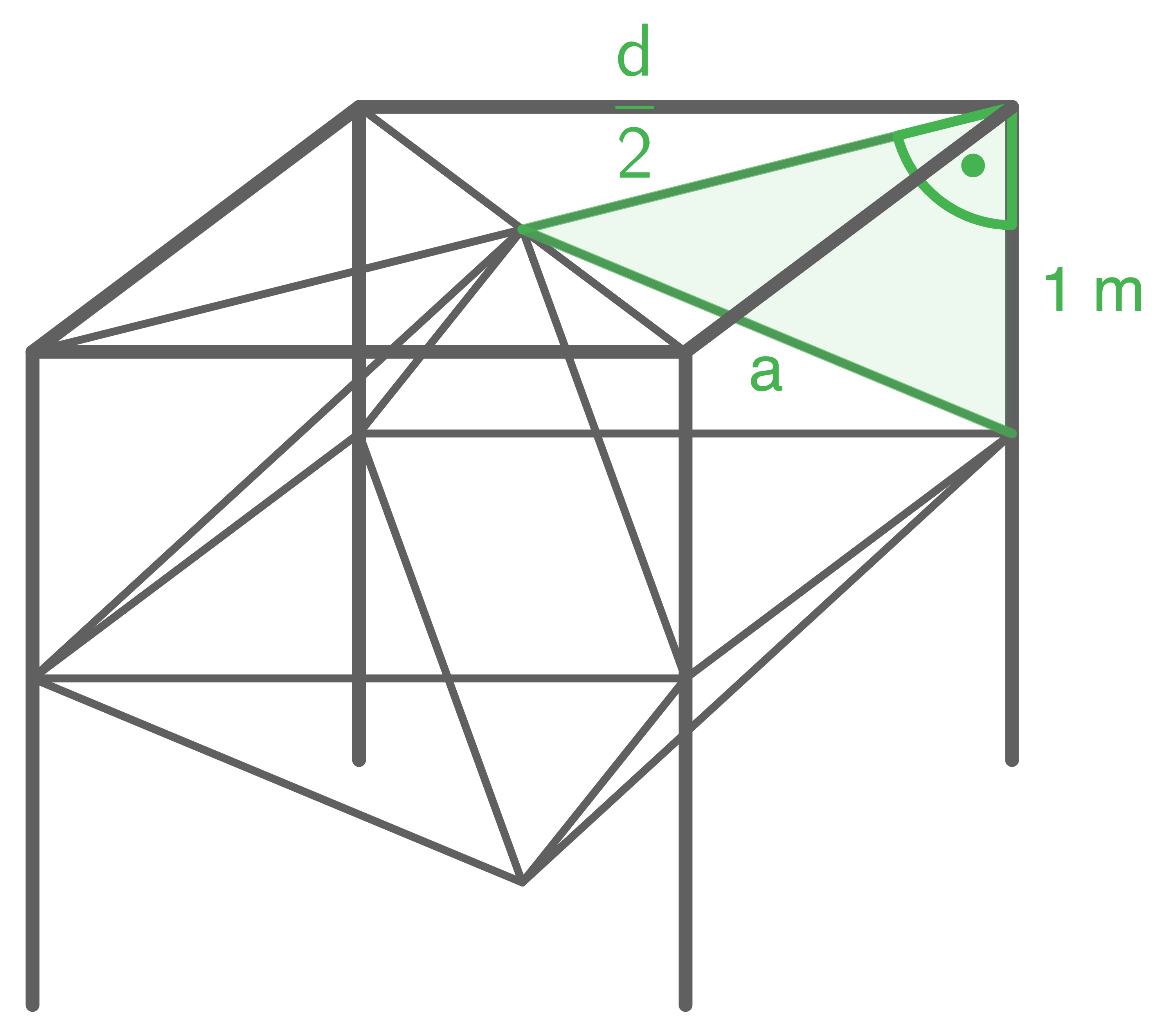
 Längen der Träger berechnen
Die oberen Endpunkte der Träger liegen auf dem Graphen von
Längen der Träger berechnen
Die oberen Endpunkte der Träger liegen auf dem Graphen von  die unteren Endpunkte auf der
die unteren Endpunkte auf der  -Achse. Die Länge der Träger entspricht also der
-Achse. Die Länge der Träger entspricht also der  -Koordinate der oberen Endpunkte.
-Koordinate der oberen Endpunkte.
Der Träger steht an der Stelle
steht an der Stelle  der Träger
der Träger  an der Stelle
an der Stelle 
![\(\begin{array}[t]{rll}
t_1:\quad p(-4)&=& \dfrac{1}{12}\cdot (-4)^2 \\[5pt]
&\approx& 1,33 \\[10pt]
t_2:\quad p(-2)&=&\dfrac{1}{12}\cdot (-2)^2 \\[5pt]
&\approx& 0,33
\end{array}\)](https://www.schullv.de/resources/formulas/96b3c6b88e408d8806cef79397b51f24fee46f9a86c0f873697b622754b44205_light.svg) Der Träger
Der Träger  ist also ca.
ist also ca.  lang, der Träger
lang, der Träger  ist ca.
ist ca.  lang.
lang.
Der Träger
c)
Richtigkeit der Pressemeldungen beurteilen
 höher als ursprünglich geplant.“
höher als ursprünglich geplant.“
1.
Grundwert 
Prozentwert
 Die erste Pressemeldung ist richtig.
Die erste Pressemeldung ist richtig.
Prozentwert
2.
Grundwert 
Prozentwert
 Die zweite Pressemeldung ist ebenfalls richtig.
Die zweite Pressemeldung ist ebenfalls richtig.
Andere mathematisch korrekte Aussage formulieren
Hier gibt es verschiedene Möglichkeiten. Eine ist beispielsweise:
„Die tatsächlichen Kosten sind Prozentwert
d)
Beim ersten Los befinden sich noch insgesamt 2 500 Lose im Lostopf. Darunter ist ein Hauptgewinn.


 Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  ist das erste verkaufte Los das Los mit dem Hauptgewinn.
Die Wahrscheinlichkeit für Ereignis
ist das erste verkaufte Los das Los mit dem Hauptgewinn.
Die Wahrscheinlichkeit für Ereignis  lässt sich mit dem Gegenereignis berechnen. Dieses lautet:
lässt sich mit dem Gegenereignis berechnen. Dieses lautet:
 „Unter den ersten drei verkauften Losen ist kein einziges Gewinnlos. “
Von den zu Beginn
„Unter den ersten drei verkauften Losen ist kein einziges Gewinnlos. “
Von den zu Beginn  Losen sind
Losen sind  Gewinnlose, es sind also
Gewinnlose, es sind also  Lose, die kein Gewinn sind. Da es sich um Ziehen ohne Zurücklegen handelt, ergibt sich folgende Rechnung:
Lose, die kein Gewinn sind. Da es sich um Ziehen ohne Zurücklegen handelt, ergibt sich folgende Rechnung:
![\(\begin{array}[t]{rll}
P(\overline{B})=& \dfrac{1\,894}{2\,500}\cdot \dfrac{1\,893}{2\,499}\cdot\dfrac{1\,892}{2\,498} \\[5pt]
\approx& 0,435 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/4eb56b71ab26f591ac07c6c98dba341a4531772a05a30fb4c29442ca77828d3b_light.svg) Die Wahrscheinlichkeit für das Ereignis
Die Wahrscheinlichkeit für das Ereignis  lässt sich damit wie folgt berechnen:
lässt sich damit wie folgt berechnen:
 Mit einer Wahrscheinlichkeit von ca.
Mit einer Wahrscheinlichkeit von ca.  befindet sich unter den ersten drei verkauften Losen mindestens ein Gewinnlos.
befindet sich unter den ersten drei verkauften Losen mindestens ein Gewinnlos.
e)
Gesamtpreis aller Gewinne berechnen:
Es müssen also 2 500€ an Gewinnen ausgeschüttet werden. Damit 2 500 € übrig bleiben, müssen die Lose insgesamt für 5 000 € verkauft werden. Jedes der 2 500 Lose muss daher für 2 € verkauft werden.