Pflichtaufgabe 2 – Mit Hilfsmitteln

Im Internet ist veröffentlicht:

„Der durchschnittliche Wertverlust über alle Pkw-Klassen hinweg beträgt bei einer Jahresfahrleistung von 15 000 Kilometern im ersten Jahr nach der Neuzulassung 24,2 Prozent. In den folgenden Jahren sind es jeweils nur rund fünf bis sechs Prozent.“

Quelle: www.focus.de (10.07.2014)

Ein PKW kostet ein Jahr nach der Neuzulassung $18\,950\,€.$
Ermittle entsprechend der Angaben aus dem Internet den Neupreis dieses PKWs.

(2 BE)

In den folgenden Jahren wird für diesen Pkw ein jährlicher Wertverlust von 6 % des jeweiligen Zeitwertes angenommen. Die Entwicklung des Zeitwertes ab dem ersten Jahr nach der Neuzulassung wird durch eine Funktion beschrieben.
Ermittle eine Gleichung dieser Funktion und gib eine zugehörige Wertetabelle mit fünf Wertepaaren an.
Stelle die Funktion in einem geeigneten Koordinatensystem graphisch dar.
Im wievielten Jahr nach dem Neukauf des Pkws sinkt sein Wert unter 10 000 Euro?

(6 BE)

Der Autohändler will eine neue Ausstellungshalle errichten. Das Dach und die Grundfläche der Halle sind Rechtecke.

Skizze nicht maßstäblich

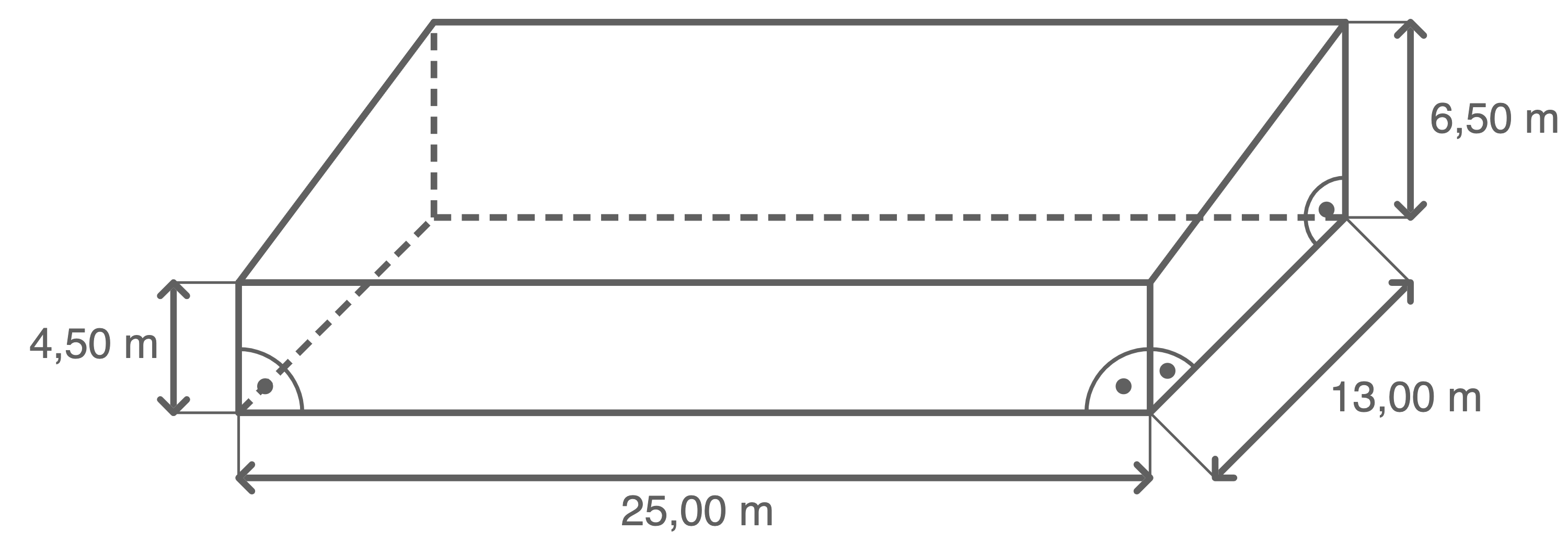Berechne das Volumen der Ausstellungshalle und den Flächeninhalt der Dachfläche.

(3 BE)

Zur Eröffnung der neuen Ausstellungshalle werden zwei Glücksräder aufgestellt. Beim einmaligen Drehen des ersten Glücksrades beträgt die Wahrscheinlichkeit eines Gewinns $\dfrac{1}{6}.$

Ein Kunde möchte das erste Glücksrad sechsmal drehen. Er sagt:
„Dann habe ich mit Sicherheit einen Gewinn.“
Hat er Recht? Begründe deine Aussage.

(1 BE)

Drei Kunden drehen nacheinander das erste Glücksrad je einmal.
Berechne die Wahrscheinlichkeit dafür, dass nur der dritte Kunde gewinnt.

(1 BE)

Drei Kunden dürfen nacheinander je einmal das zweite Glücksrad drehen.

Peter hat berechnet, dass die Wahrscheinlichkeit dafür, dass nur der zweite Kunde gewinnt, $12,8 \,\%$ beträgt.
Beschreibe, wie dieses Glücksrad aussehen kann. Begründe.

(2 BE)

Der Wertverlust eines Pkws beträgt im ersten Jahr $24,2 \,\%.$ Der Pkw kostet nach dem ersten Jahr $18\,950 \,€,$ was $100\,\%-24,2\,\%=75,8\,\%$ des Neupreises entspricht. Damit folgt:

$\begin{array}[t]{rll} \dfrac{N}{100\,\%}&=& \dfrac{18\,950\,€}{75,8\,\%} \quad \scriptsize \mid\; \cdot 100\,\% \\[5pt] N&=& \dfrac{18\,950\,€}{75,8\,\%}\cdot 100\,\% \\[5pt] N&=& 25\,000\,€ \end{array}$

Der Neupreis des Pkws beträgt $25 \,000 \,€.$

Funktionsgleichung ermitteln

Der Wert des Pkws nach dem ersten Jahr kann durch eine Exponentialfunktion der Form $p_t=f(t)=p_0\cdot a^t$ beschrieben werden. Dabei ist $p_t$ der Wert nach $t$ Jahren nach dem ersten Jahr, $p_0$ der Wert nach dem ersten Jahr, $a$ die Abnahme und $t$ die Zeit in Jahren nach dem ersten Jahr der Neuzulassung.

Es gilt:

$a=1-0,06=0,94$
$p_0=18\,950\,€$

Damit ergibt sich die folgende Funktionsgleichung:

$p_t=f(t)=18\,950\cdot 0,94^t$

Wertetabelle erstellen

Ein Wertetabelle kann mit dem Taschenrechner bestimmt werden. Es ergibt sich (gerundet auf ganze Euro):

$\color{#ffffff}{t}$ in Jahren	$\color{#ffffff}{p_t}$ in €
$0$	$18\,950$
$1$	$17\,813$
$2$	$16\,744$
$3$	$15\,740$
$4$	$14\,795$

Funktion graphisch darstellen

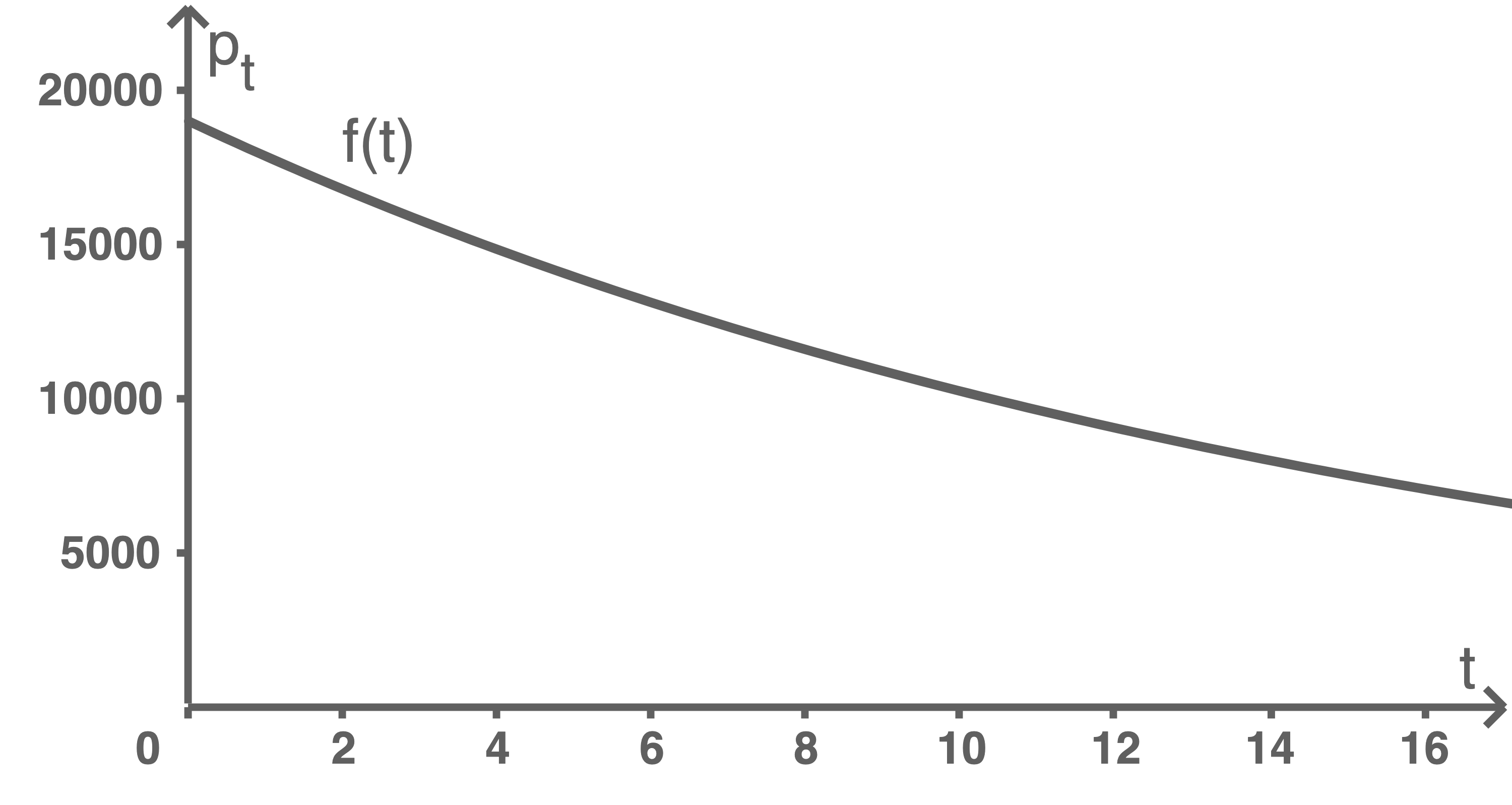Bestimmen, wann der Wert unter $\boldsymbol {10\,000\,€}$ Euro sinkt

Um zu bestimmen, im wievielten Jahr der Wert unter $10\,000\,€$ sinkt, muss die folgende Ungleichung gelöst werden:

$f(t)=18\,950\cdot 0,94^t\lt 10\,000$

Der Taschenrechner liefert $x\approx 10,3.$ Hinzu kommt noch das erste Jahr nach der Neuzulassung.

Nach ungefähr 11,3 Jahren ist der Wert auf $10\,000\,€$ gesunken. Daher fällt der Wert des Autos im 12. Jahr nach dem Kauf auf unter $10\,000\,€.$

Volumen der Halle berechnen

Die Halle hat die Form eines Prismas, dessen Grundfläche ein Trapez ist. Um das Volumen des Prismas zu berechnen, wird zunächst der Flächeninhalt des Trapezes bestimmt.

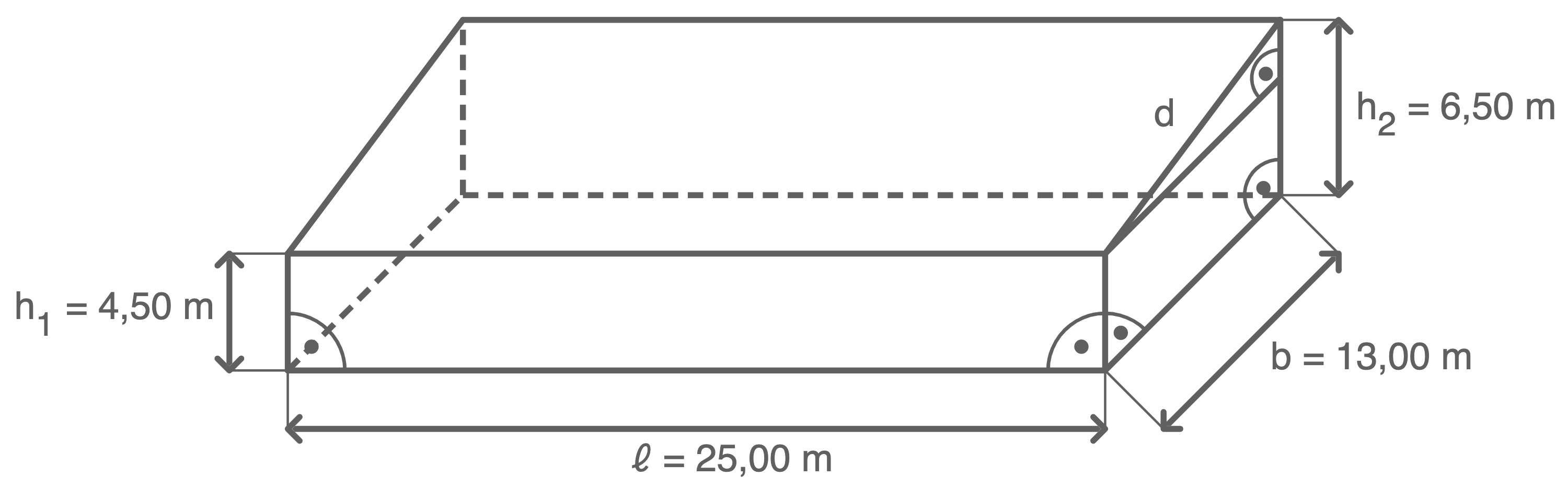
$\begin{array}[t]{rll} A_T&=& \dfrac{h_1+h_2}{2}\cdot b \\[5pt] &=&\dfrac{4,50\,\text{m}+6,50\,\text{m}}{2}\cdot 13,00\,\text{m} \\[5pt] &=& 71,5 \,\text{m}^2 \end{array}$

Das Volumen des Prismas kann nun wie folgt berechnet werden:

$\begin{array}[t]{rll} V&=& A_T\cdot \ell \\[5pt] &=& 71,50\,\text{m}^2 \cdot 25,00\,\text{m} \\[5pt] &=& 1\,787,5 \,\text{m}^3 \end{array}$

Das Volumen der Halle beträgt $1\,787,5\,\text{m}^3.$

Flächeninhalt der Dachfläche berechnen

Um den Flächeninhalt der Dachfläche zu bestimmen, muss zunächst die Länge der Dachkante $d$ bestimmt werden. Mit dem Satz des Pythagoras gilt:

$\begin{array}[t]{rll} d^2&=& b^2+(h_2-h_1)^2\\[5pt] d^2 &=& (13\,\text{m})^2+(2\,\text{m})^2 \\[5pt] d^2&=& 173\,\text{m}^2 \quad \scriptsize\mid\; \sqrt{\;}\\[5pt] d&=&\sqrt{173}\,\text{m}\\[5pt] d&\approx& 13,15\,\text{m} \\[5pt] \end{array}$

Die Fläche des Dachs ist rechteckig. Es folgt:

$\begin{array}[t]{rll} A&=& \ell\cdot d\\[5pt] &\approx& 25\,\text{m}\cdot 13,15\,\text{m}\\[5pt] &\approx& 329\,\text{m}^2 \end{array}$

Der Flächeninhalt der Dachfläche beträgt ungefähr $329\,\text{m}^2.$

Der Kunde hat nicht recht. Bei jedem Drehvorgang beträgt die Wahrscheinlichkeit $\dfrac{1}{6}.$ Der Kunde kann also sechsmal drehen und trotzdem nicht gewinnen.

Bei einer Drehung des Glücksrads gelten die folgenden Wahrscheinlichkeiten:

$P(\text{„Gewinn“})=P(G)=\dfrac{1}{6}$

$P(\text{„Kein Gewinn“})=P(\overline{G})=1-\dfrac{1}{6}=\dfrac{5}{6}$

Mit der Pfadmultiplikationsregel folgt:

$\begin{array}[t]{rll} P(\overline{GG}G)&=&\dfrac{5}{6}\cdot\dfrac{5}{6}\cdot \dfrac{1}{6}\\[5pt] &=& \dfrac{25}{216}\\[5pt] &\approx& 0,116\\[5pt] \end{array}$

Die Wahrscheinlichkeit, dass nur der dritte Kunde gewinnt, beträgt ungefähr $11,6\,\%.$

$P(\text{„Gewinn“})=P(G)=p$

Bekannt ist:

$\begin{array}[t]{rll} P(\overline{G}G\overline{G})&=& 0,128 \\[5pt] (1-p)\cdot p\cdot (1-p)&=& 0,128 \end{array}$

Der Taschenrechner liefert die Lösungen $p_1=0,2,$ $p_2\approx 0,49$ und $p_3\approx 1,31.$ Wegen $p_3\gt 1$ entfällt diese Lösung im Sachzusammenhang.

Ein mögliches Glücksrad könnte für die Lösung $p_1=0,2$ wie folgt aussehen:

Das Glücksrad hat 5 gleich große Sektoren, die demnach alle die Wahrscheinlichkeit $p=\dfrac{1}{5}=0,2$ haben. Auf einem dieser Segmente steht „Gewinn“.