Pflichtaufgabe 2 – Mit Hilfsmitteln
1.
Im Märchen „Hans und die Bohnenranke“ wächst eine Zauberbohne innerhalb eines Tages bis zum Himmel.
Hans beschreibt dieses Wachstum mathematisch mit der Gleichung
, wobei 
die Zeit seit Beginn des Wachstums in Stunden und 
die Höhe der Bohnenranke in Meter ist.
Hans beschreibt dieses Wachstum mathematisch mit der Gleichung
a)
Stelle das Wachstum der Bohnenranke für die ersten 10 Stunden graphisch dar.
(2 BE)
b)
Ermittle die Zeit, nach der die Bohnenranke ein Meter hoch ist.
(2 BE)
c)
Bestimme die durchschnittliche Wachstumsgeschwindigkeit der Bohnenranke in 
in der elften Stunde.
(2 BE)
2.
Dargestellt ist der Querschnitt eines Dachbodens.
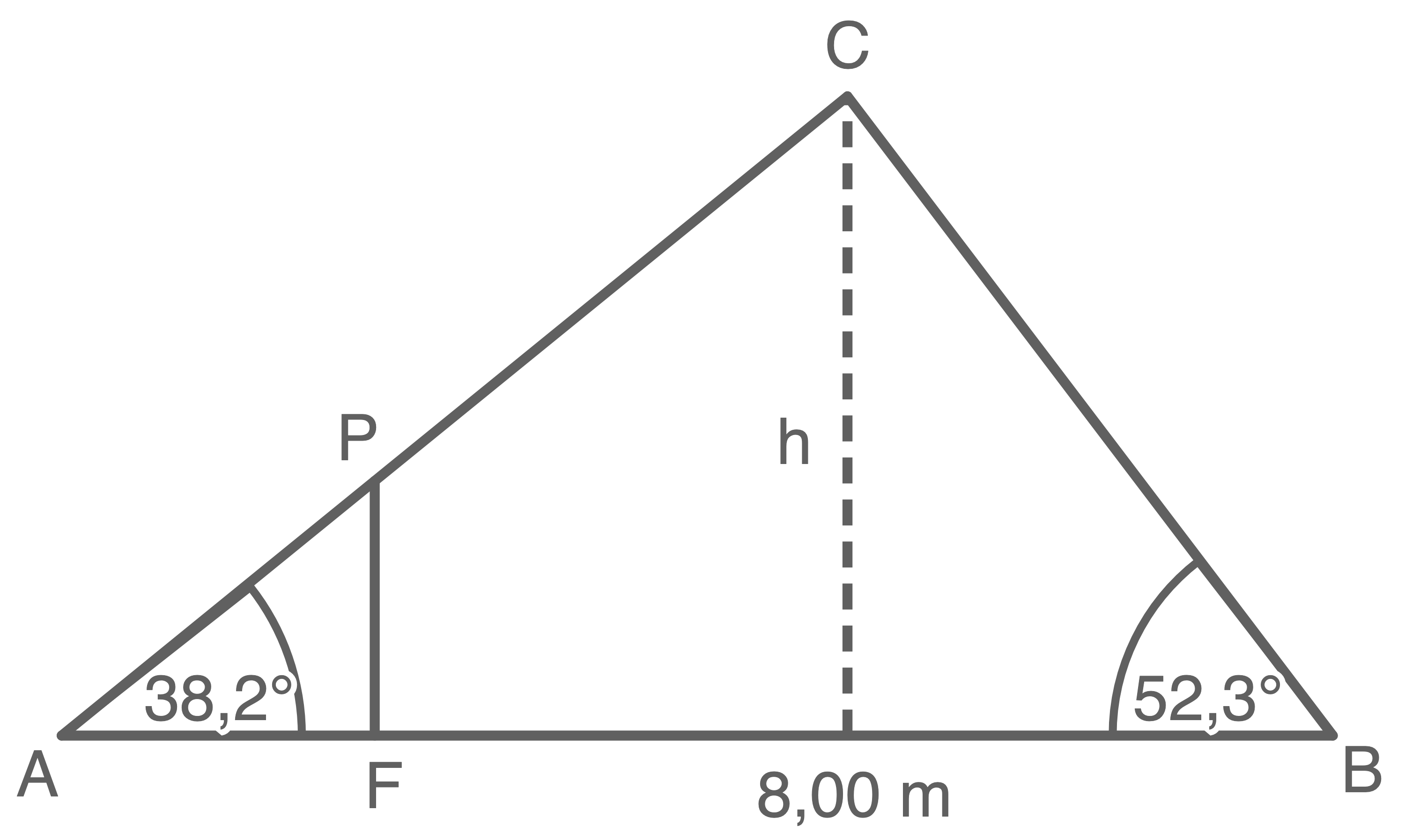
Skizze nicht maßstäblich
a)
Berechne die Höhe h des Dachbodens.
(5 BE)
b)
Im Dachboden soll eine senkrechte 
hohe Wand eingebaut werden, die in der Skizze durch die Strecke 
veranschaulicht ist.
Berechne den Abstand der Wand von der Stelle, die durch den Punkt A dargestellt wird.
(2 BE)
3.
In den letzten Jahren betrug der Anteil der Mädchen an allen geborenen Kindern in Deutschland etwa 49
%. Ein Meinungsforschungsinstitut befragt zufällig Mütter mit drei Kindern.
a)
Berechne die Wahrscheinlichkeit folgender Ereignisse:
A: = „Das erste Kind einer befragten Mutter ist ein Mädchen, das zweite und dritte jeweils ein Junge.“
B: = „Eine befragte Mutter hat mindestens ein Mädchen.“
(4 BE)
b)
Weise nach, dass bei etwa einem Viertel aller Mütter mit drei Kindern alle Kinder das gleiche Geschlecht haben.
Berechne die Wahrscheinlichkeit dafür, dass unter zehn befragten Müttern keine Mutter ist, deren Kinder alle das gleiche Geschlecht haben.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
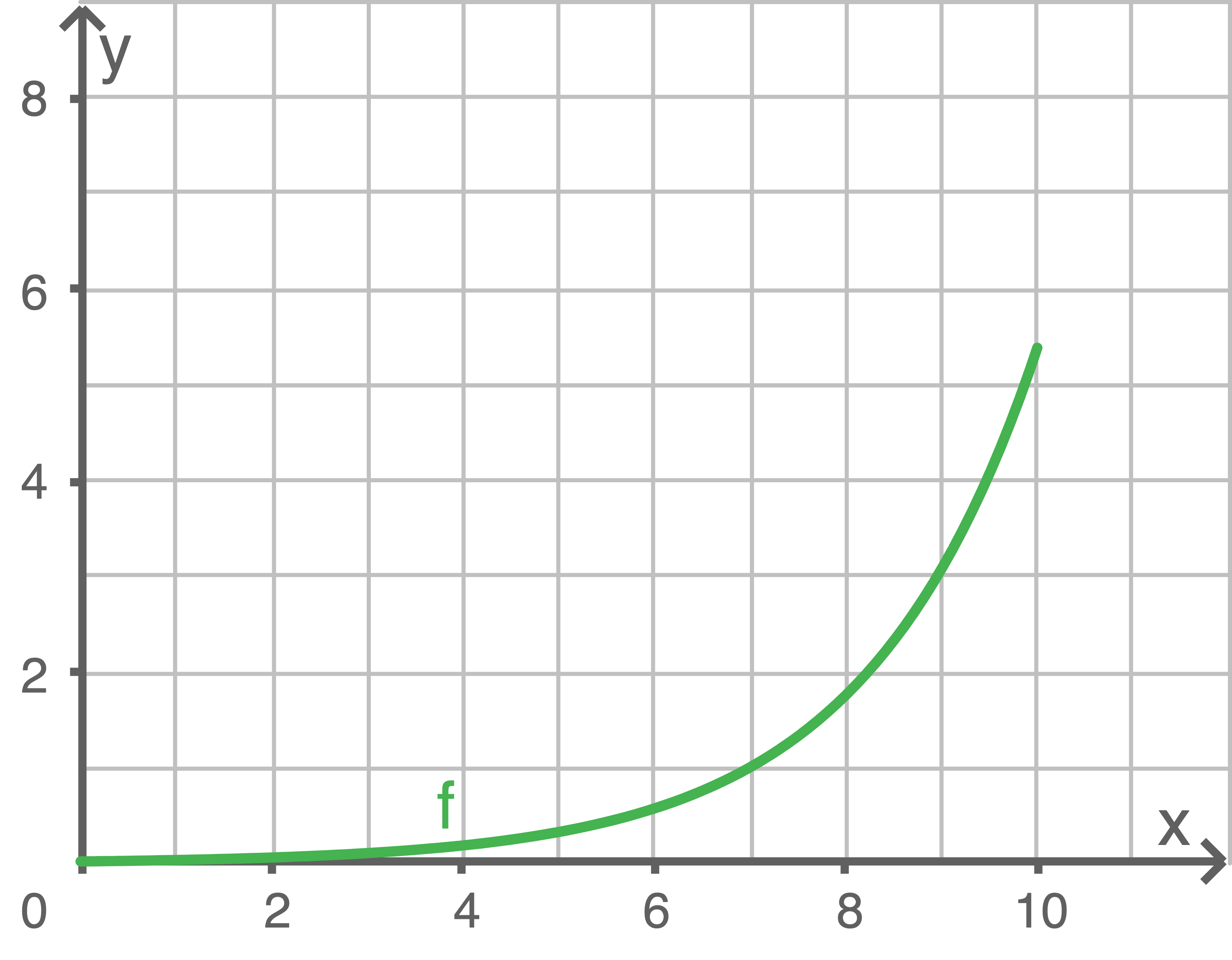
b)
c)
2.
a)
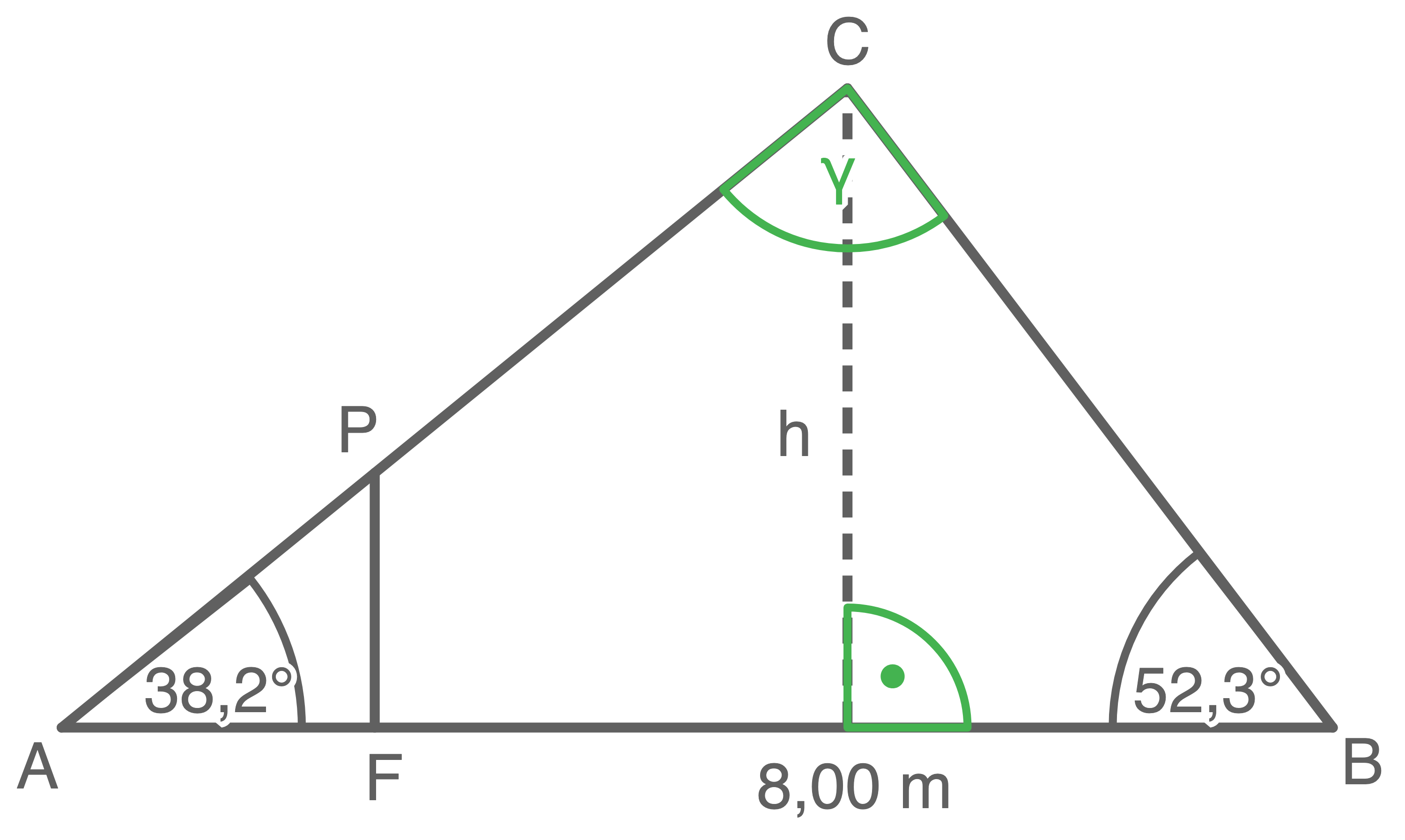
b)
In dem rechtwinkligen Dreieck 
gilt:
![\(\begin{array}[t]{rll}
\tan(\alpha)&=& \dfrac{\overline{PF}}{\overline{AF}} \quad \scriptsize \mid\; \cdot \overline{AF} \\[5pt]
\tan(\alpha)\cdot \overline{AF}&=& \overline{PF} \quad \scriptsize \mid\; :\tan(\alpha) \\[5pt]
\overline{AF}&=& \dfrac{\overline{PF}}{\tan(\alpha)} \quad \scriptsize \mid\; \\[5pt]
\overline{AF}&=& \dfrac{1,50\,\text{m}}{\tan(38,2°)} \quad \scriptsize \mid\; \\[5pt]
\overline{AF}&\approx& 1,91\,\text{m}
\end{array}\)](https://mathjax.schullv.de/2dff16ddecfb50d90ecba498e7f25cc4c1edc087b7ef8837741361e2a03b10e2?color=5a5a5a)
3.
a)
b)
Nachweisen, dass bei etwa einem Viertel aller Mütter mit drei Kindern alle Kinder das gleiche Geschlecht haben
![\(\begin{array}[t]{rll}
&=& P(\text{dreimal M})+P(\text{dreimal J}) \\[5pt]
&=& 0,49\cdot 0,49\cdot 0,49+0,51\cdot 0,51\cdot 0,51 \\[5pt]
&=& 0,2503 \\[5pt]
&\approx& \dfrac{1}{4}
\end{array}\)](https://mathjax.schullv.de/3624aaaab4c6a73c383d21003bebb602354538b2afad3d48df0335b75bb7e9d1?color=5a5a5a)
Die Wahrscheinlichkeit dafür, dass unter zehn befragten Müttern keine Mutter ist, deren Kinder alle das gleiche Geschlecht haben, berechnen
Die Wahrscheinlichkeit dafür, dass die Kinder nicht das gleiche Geschlecht haben, beträgt 
Damit folgt:
![\(\begin{array}[t]{rll}
P(\text{keine Mutter dabei mit GG})&=& \left(\dfrac{3}{4}\right)^{10} \\[5pt]
&=& 0,0563 \\[5pt]
&=& 5,63\,\%
\end{array}\)](https://mathjax.schullv.de/f6b93e5eccfe0a93979d018e27729ccbbe6d1b37ae9d70d0c8484a1680c38ac2?color=5a5a5a)