Pflichtaufgabe 1 – Ohne Hilfsmittel
1.
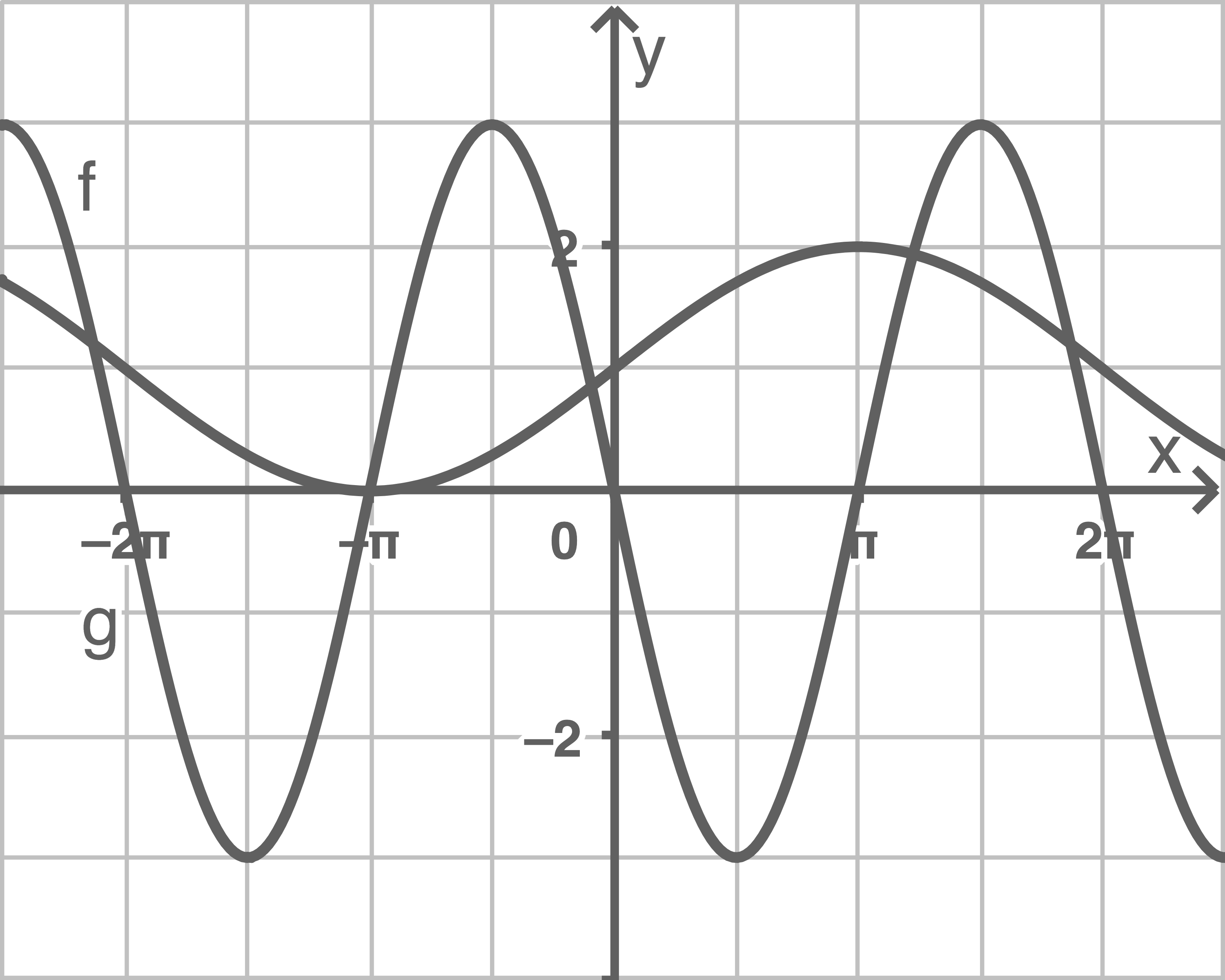
Skizziere die Graphen der Funktionen
 und
und 
im Intervall in ein Koordinatensystem.
in ein Koordinatensystem.
im Intervall
(4 BE)
2.
Berechne.





(5 BE)
3.
Eine Lernerfolgskontrolle ergab folgende Notenverteilung.
| Note | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Anzahl | 4 | 6 | 7 | 5 | 3 | 0 |
a)
Vervollständige das Streifendiagramm (mit Beschriftung).


(3 BE)
b)
Berechne den prozentualen Anteil der Lernenden, deren Noten besser als der Durchschnitt sind.
(3 BE)
4.
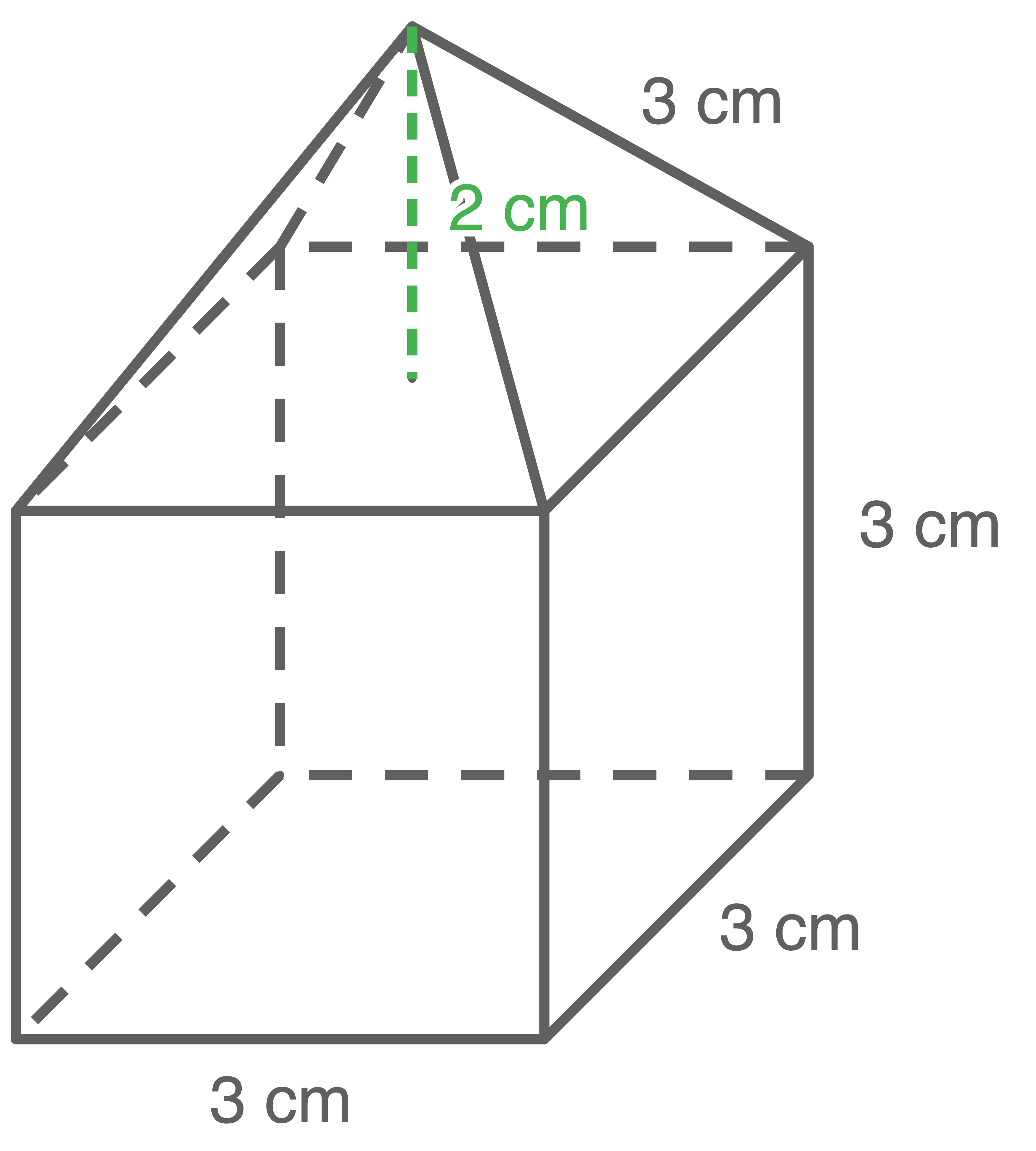
Einem Würfel mit der Kantenlänge  wird eine gerade quadratische Pyramide mit derselben Grundkantenlänge und der Höhe
wird eine gerade quadratische Pyramide mit derselben Grundkantenlänge und der Höhe  aufgesetzt.
aufgesetzt.
a)
Zeichne ein Schrägbild dieses Körpers auf weißem Papier.
(3 BE)
b)
Berechne das Volumen dieses Körpers.
(2 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
2.
3.
a)

- Gesamtlänge des Streifendiagramms:
(Hinweis: Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.) - Gesamtanzahl der Noten:
b)
Durchschnitt berechnen
Prozentualen Anteil berechnen
Anzahl der Lernenden, deren Noten besser als der Durchschnitt sind:  Anteil an allen 25 Schüler*innen:
Anteil an allen 25 Schüler*innen:
 Der prozentuale Anteil der Lernenden, deren Noten besser als der Durchschnitt sind, liegt bei 40 %.
Der prozentuale Anteil der Lernenden, deren Noten besser als der Durchschnitt sind, liegt bei 40 %.
a)
b)