Pflichtaufgabe 1 – Ohne Hilfsmittel
1.
Berechne die folgenden Terme so weit wie möglich.
(5 BE)
2.
Gegeben ist eine gerade Pyramide (siehe Abbildung) mit rechteckiger Grundfläche.
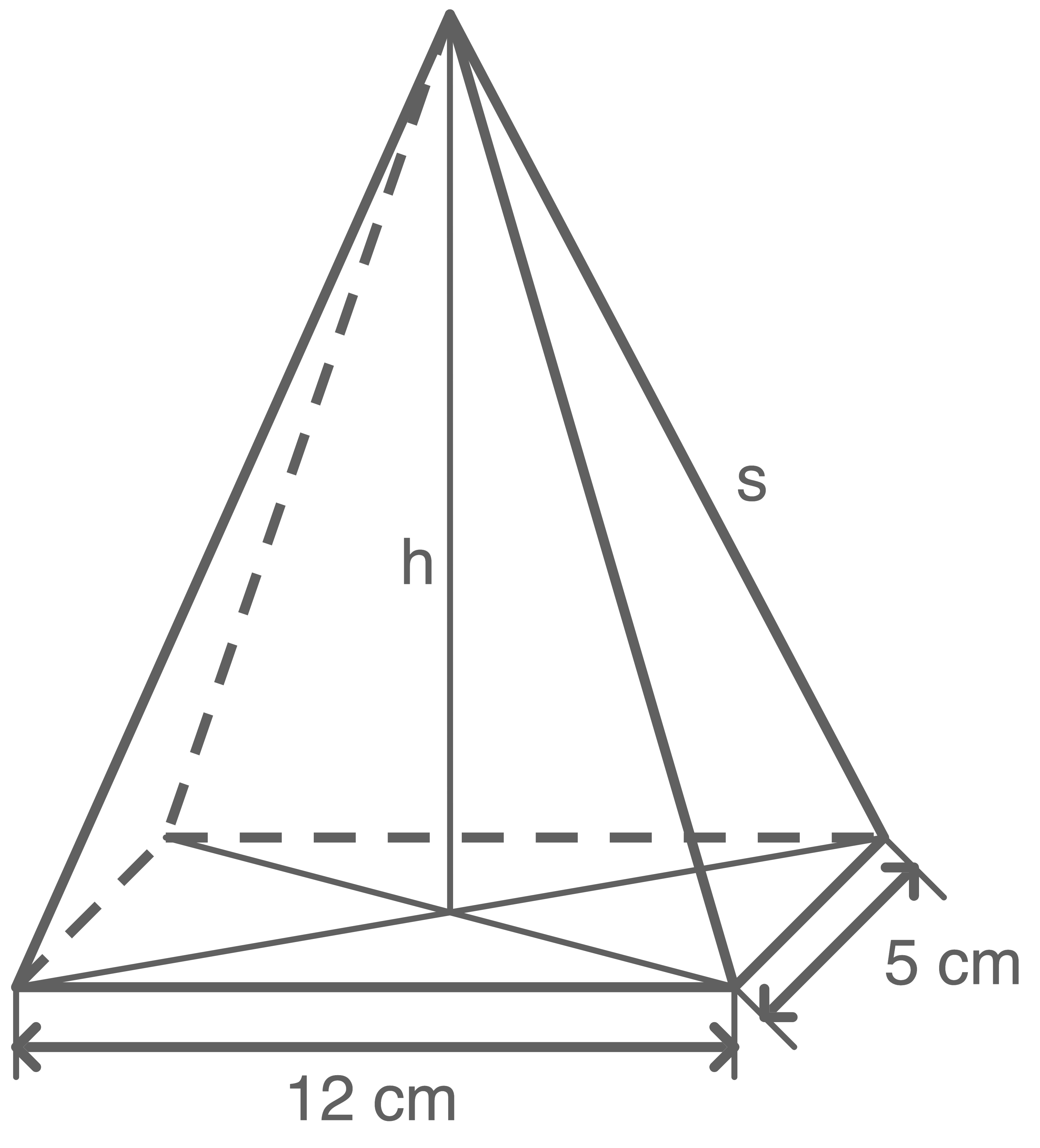
a)
Das Volumen der Pyramide beträgt 
Berechne die Höhe der Pyramide.
Berechne die Höhe der Pyramide.
(2 BE)
b)
Die Länge der Grundkanten 
bzw. 
und die Körperhöhe 
sind bekannt.
Beschreibe ein Vorgehen, mit dem die Länge der Seitenkante
der Pyramide berechnet werden kann.
Beschreibe ein Vorgehen, mit dem die Länge der Seitenkante
(3 BE)
3.
Gegeben sind die Funktionen 
und 
mit 
und 
für 
a)
Zeichne die Graphen von und im Intervall 
(3 BE)
b)
Gib 
an.
Begründe deine Überlegungen.
Begründe deine Überlegungen.
(2 BE)
4.
In einem Beutel befinden sich 20 Kugeln. Davon sind zehn blau, sieben gelb und die restlichen rot. Paul zieht zufällig eine Kugel, stellt die Farbe fest, legt die Kugel wieder zurück und zieht danach ein zweites Mal.
a)
Berechne die Wahrscheinlichkeit folgender Ereignisse:
„Paul zieht nur gelbe Kugeln."
„Paul zieht Kugeln mit unterschiedlicher Farbe.“
(3 BE)
b)
Beschreibe ein Ereignis 
für das gilt:
(2 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
2.
a)
Mit der Formel für das Volumen einer Pyramide gilt:
![\(\begin{array}[t]{rll}
V&=& \dfrac{1}{3}\cdot G\cdot h \\[5pt]
300\,\text{cm}^3&=& \dfrac{1}{3}\cdot 12\,\text{cm}\cdot 5\,\text{cm}\cdot h \\[5pt]
300\,\text{cm}^3&=& 20\,\text{cm}^2\cdot h \quad \scriptsize \mid\; :20\,\text{cm}^2 \\[5pt]
15\,\text{cm}&=& h
\end{array}\)](https://mathjax.schullv.de/873155cd6aacfb97663aa877619cf978ce37fd6a148fe6508f14c6283d08f767?color=5a5a5a)
Die Pyramide ist 
hoch.
b)
Die halbe Diagonale der Grundfläche 
kann mit dem Satz des Pythagoras berechnet werden:
Damit kann wieder mit dem Satz des Pythagoras die Länge der Seitenkante wie folgt berechnet werden:
![\(\begin{array}[t]{rll}
s^2&=& \left(\dfrac{d}{2}\right)^2+h^2 \\[5pt]
s^2&=& \left(\dfrac{a}{2}\right)^2+\left(\dfrac{b}{2}\right)^2+h^2 \quad \scriptsize \mid\;\sqrt{\,} \\[5pt]
s&=& \sqrt{\left(\dfrac{a}{2}\right)^2+\left(\dfrac{b}{2}\right)^2+h^2}
\end{array}\)](https://mathjax.schullv.de/af3c5328418b5c06eaf768f7a03f0ee6833ac76cb835ffce069fbcf93c159ebf?color=5a5a5a)
3.
a)
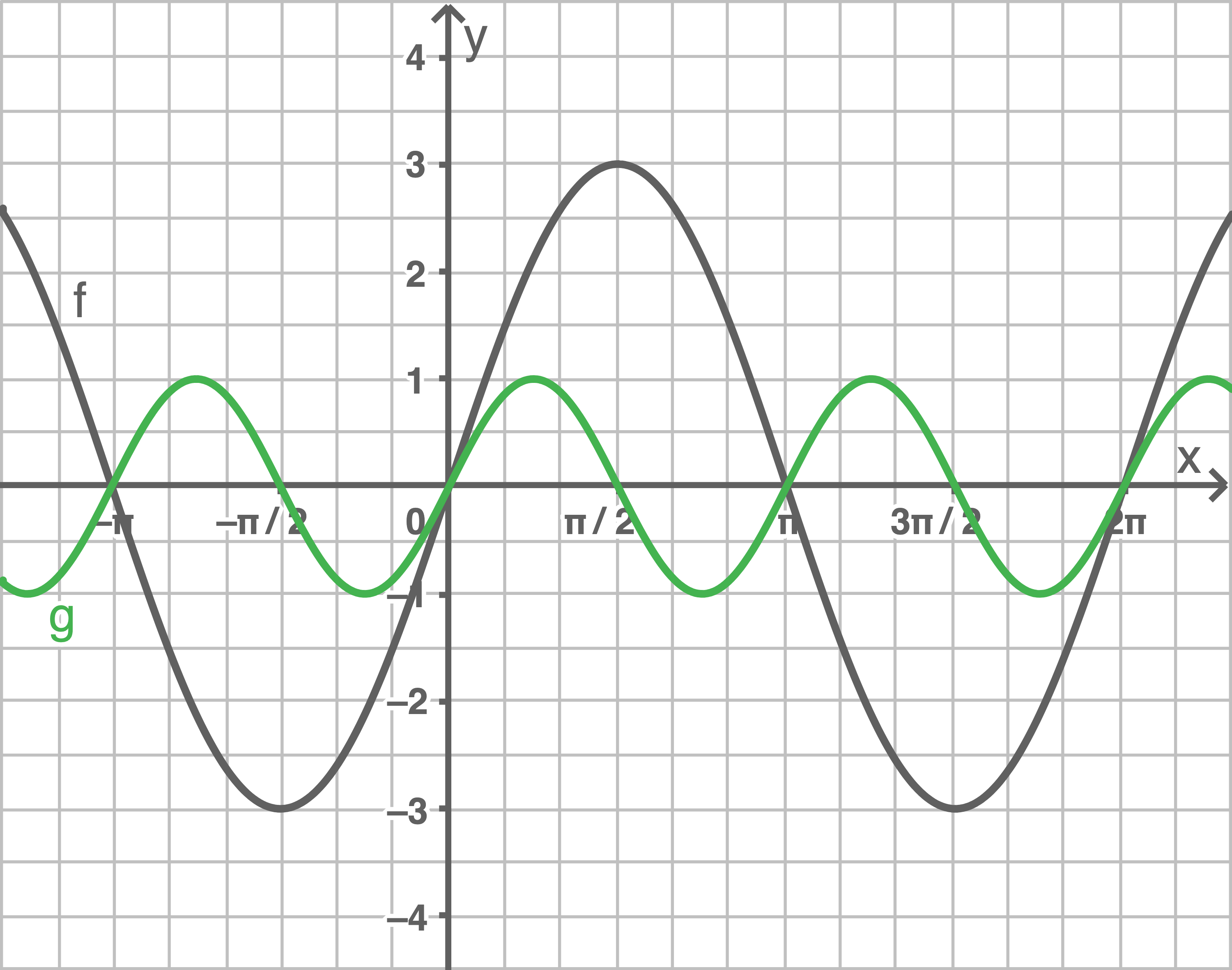
b)
4.