Pflichtaufgabe 1 – Ohne Hilfsmittel
1.
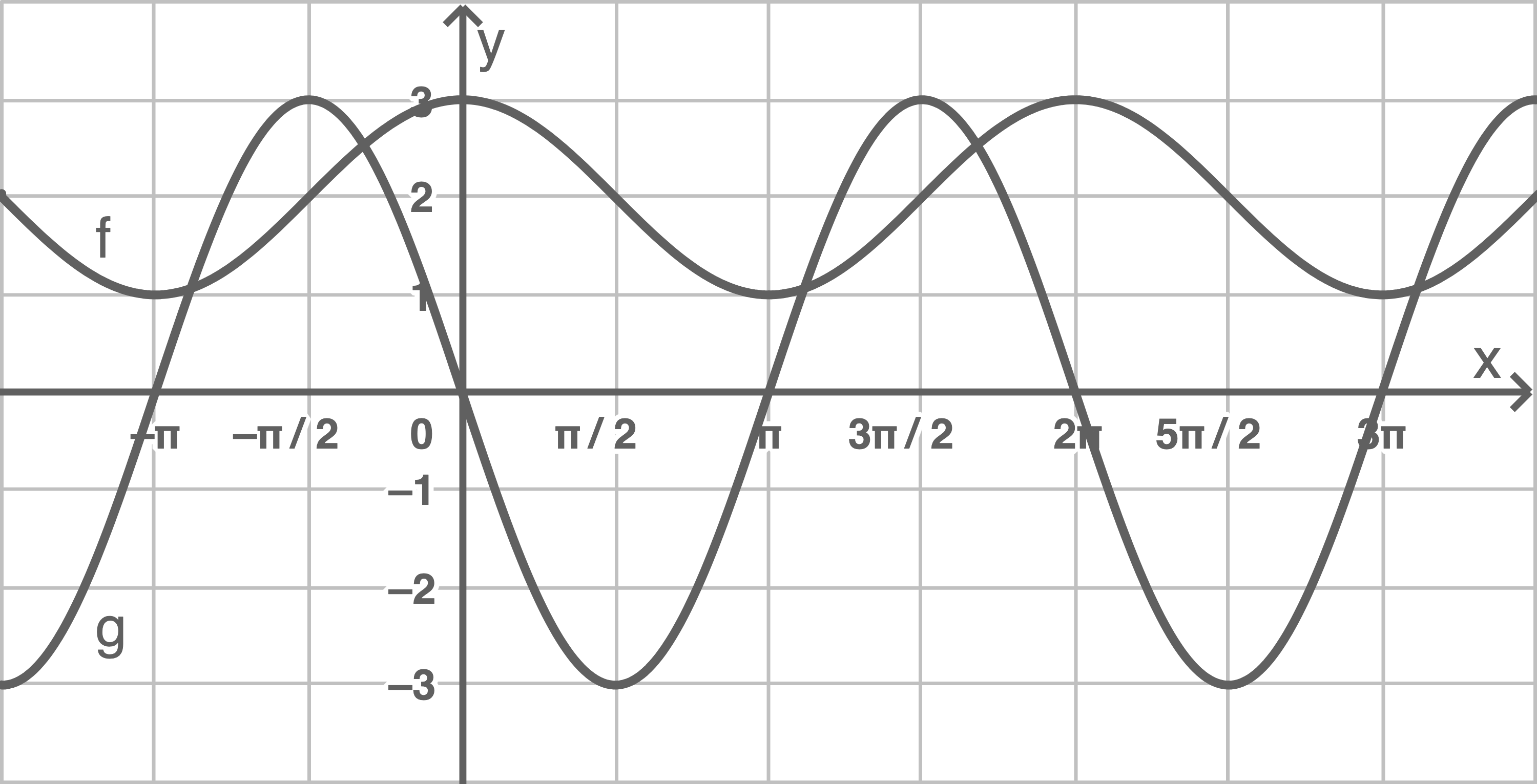
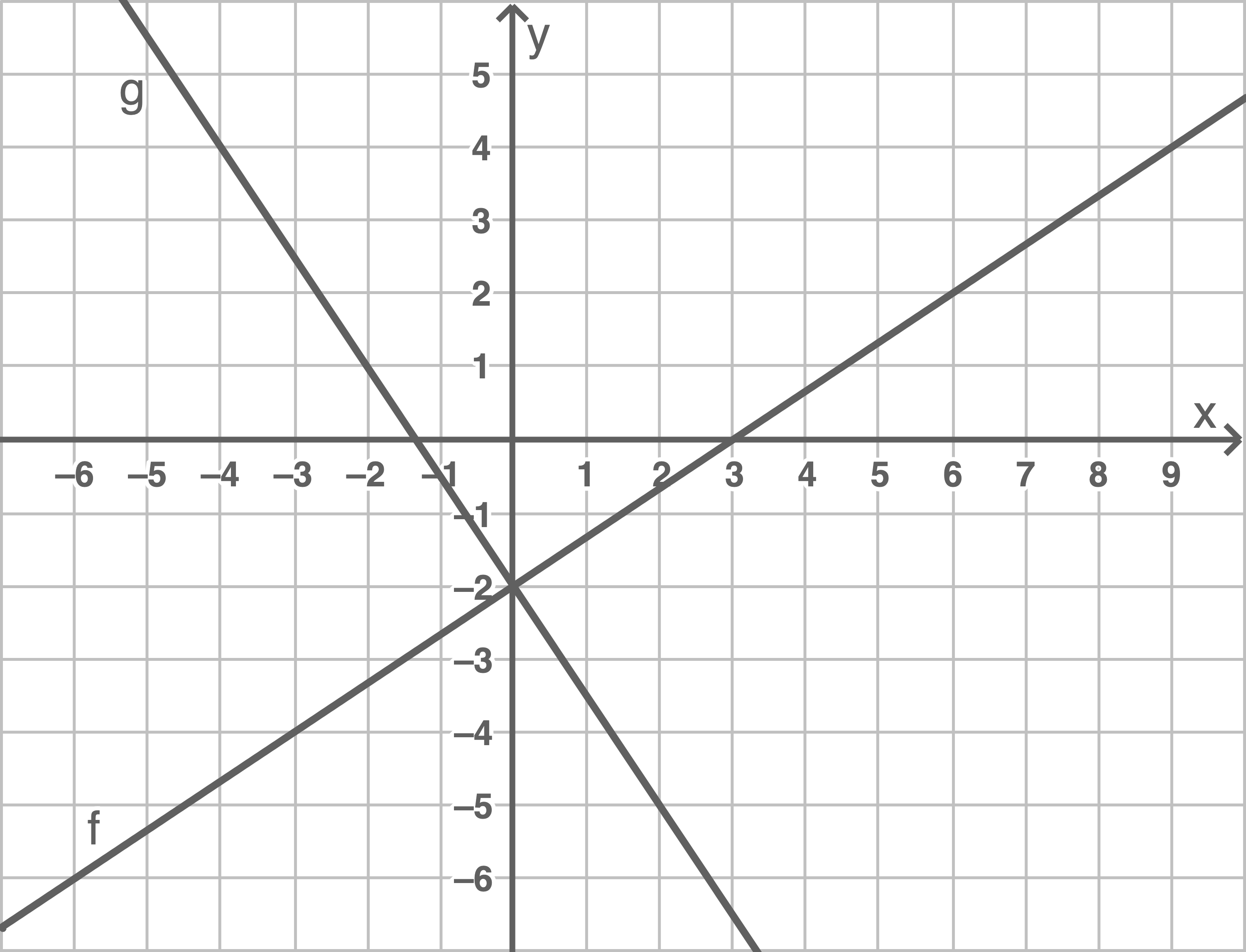
Gib je eine Gleichung der dargestellten Funktionen 
und 
an.
(2 BE)
2.
Gegeben ist die Funktion durch 
.
Der Graph der Funktion ist eine Gerade, die senkrecht zum Graphen von verläuft. Die Graphen von und schneiden sich in einem Punkt auf der 
-Achse.
a)
Zeichne die Graphen von und in ein Koordinatensystem.
(2 BE)
b)
Gib eine Funktionsgleichung von an.
(1 BE)
3.
Leon möchte die Breite eines Sees bestimmen und fertigt eine Skizze an.
Die gestrichelten Linien verlaufen parallel.
Berechne die Breite des Sees.
Die gestrichelten Linien verlaufen parallel.
Berechne die Breite des Sees.
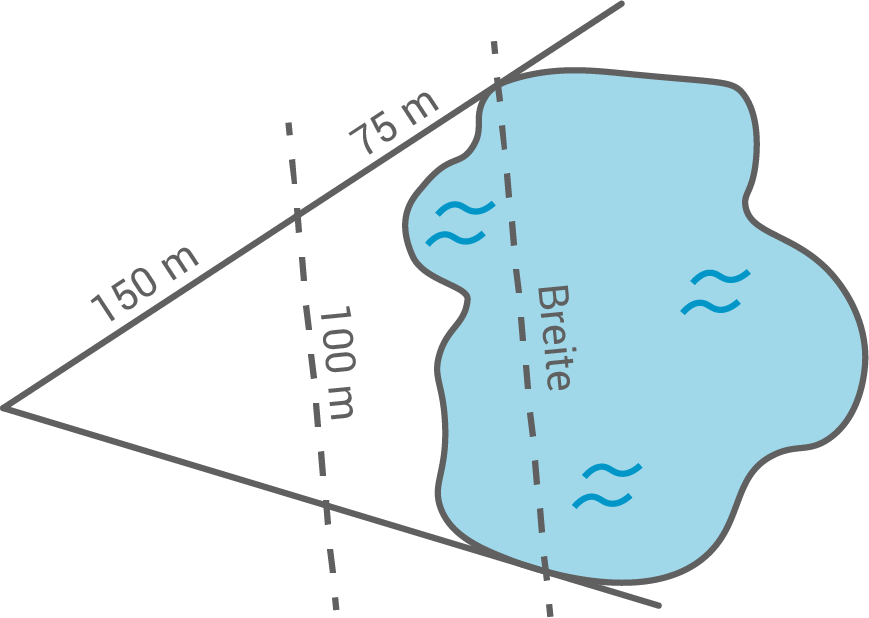
Skizze nicht maßstäblich
(2 BE)
4.
Gegeben ist ein Zylinder mit dem Radius 
und der Höhe 
Bei einem zweiten Zylinder sind der Radius doppelt und die Höhe halb so groß wie beim ersten Zylinder.
Begründe, dass das Volumen des zweiten Zylinders doppelt so groß wie das Volumen des ersten Zylinders ist.
Begründe, dass das Volumen des zweiten Zylinders doppelt so groß wie das Volumen des ersten Zylinders ist.
(1 BE)
5.
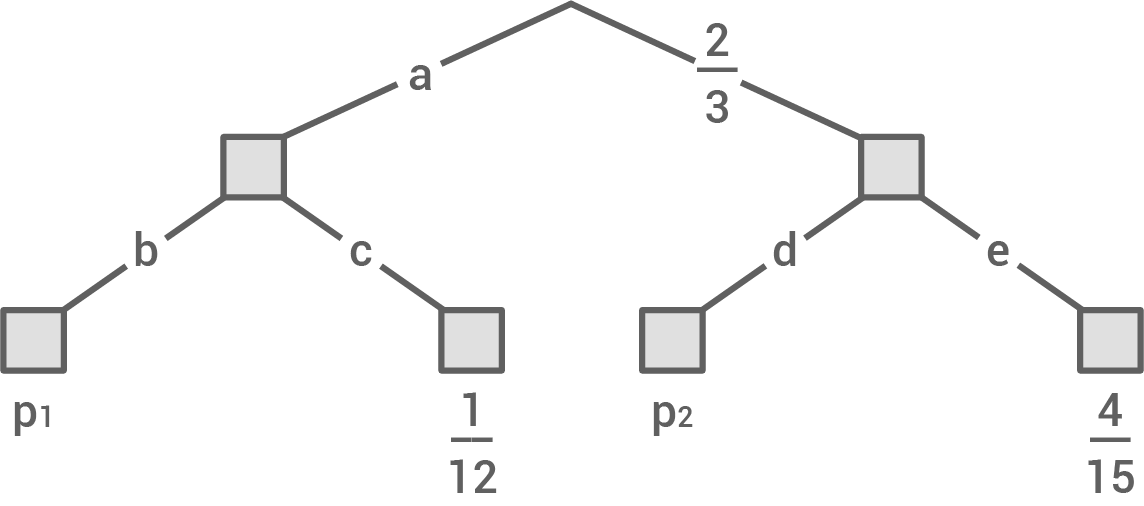
Gegeben ist für ein Zufallsexperiment ein Baumdiagramm.
Bestimme die Wahrscheinlichkeiten
und 
.
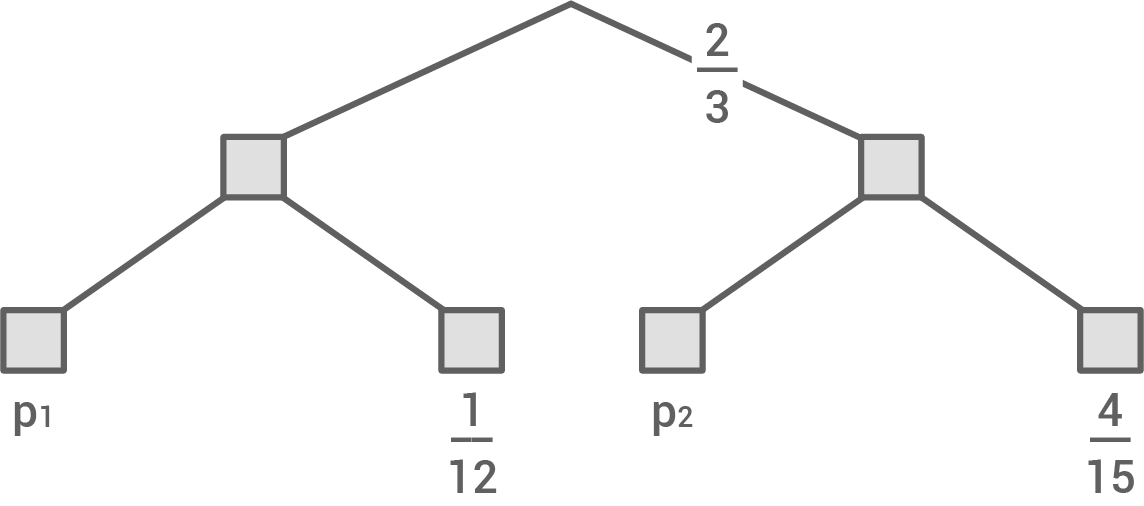
Bestimme die Wahrscheinlichkeiten
(2 BE)
1.
Der Graph von bildet eine um 
Einheiten nach oben verschobene Kosinusfunktion ab:
Der Graph von bildet eine gespiegelte und um den Faktor 
gestreckte Sinusfunktion ab:
2.
a)
b)
Die Steigung 
und die Verschiebung um Einheiten nach unten lassen sich aus der Abbildung aus Teilaufgabe a) ablesen.
Die Funktionsgleichung von lautet 
3.
Die Breite 
des Sees lässt sich mit dem Strahlensatz berechnen.
![\(\begin{array}[t]{rll}
\dfrac{150\,\text{m}}{100\,\text{m}}&=& \dfrac{150\,\text{m}+75\,\text{m}}{x} \\[5pt]
\dfrac{3}{2}&=& \dfrac{225\,\text{m}}{x} \quad \scriptsize \mid\;\cdot 2x \\[5pt]
3x&=& 450\,\text{m} \quad \scriptsize \mid\;:3 \\[5pt]
x &=& 150\,\text{m}
\end{array}\)](https://mathjax.schullv.de/eaf71c8098c315b7c812a2dfd2df24cdd7eb621b8ac790e0abf056c44572b6b2?color=5a5a5a)
Der See ist 150 Meter breit.
4.
Die Formel zur Berechnung des Volumens des ersten Zylinders lautet:
Der Radius des zweiten Zylinders ist nun doppelt so groß und die Höhe halb so groß, deshalb ergibt sich:
![\(\begin{array}[t]{rll}
V_2&=& \pi \cdot (2r)^2 \cdot \dfrac{h}{2} \\[5pt]
&=& \pi\cdot 4\cdot r^2\cdot \dfrac{h}{2} \\[5pt]
&=& 2 \cdot \pi \cdot r^2 \cdot h \\[5pt]
&=& 2\cdot V_1
\end{array}\)](https://mathjax.schullv.de/8f361c12a5da94bdd992fc02f8810b3903bae287019acb5af6258549f39ccf78?color=5a5a5a)
Das Volumen des zweiten Zylinders ist doppelt so groß.
5.
