Wahlaufgabe 2

In der Tabelle wurden die Umsätze eines Gartenmarktes erfasst.

Jahr	2013	2014	2015
Umsatz in Millionen Euro	1,54	2,10	2,86

Der Leiter dieses Gartenmarktes stellt fest, dass pro Jahr etwa 10 % vom Umsatz als Gewinn erwirtschaftet wurden.
Berechne den gesamten Gewinn des Gartenmarktes für die Jahre 2013 bis 2015.

(1 BE)

Der Umsatz in Millionen Euro soll durch eine Funktion $q$ der Form $q(x) = a\cdot x^2 + b\cdot x + c$ $(a, b, c, x \in \mathbb{R}; a\neq 0)$ mathematisch beschrieben werden. Dabei gibt $x$ die Anzahl der Jahre an, die seit 2012 vergangen sind.
Bestimme unter Verwendung der Funktionsgleichung von $q$ den Umsatz in den Jahren 2016 und 2020.
Beurteile, ob mithilfe der Funktion $q$ Prognosen für eine zukünftige Entwicklung der Umsätze sinvoll sind.

(5 BE)

Der Gartenmarkt erhält eine große Menge unsortierter Tulpenzwiebeln. Ein Viertel dieser Zwiebeln bringt zweifarbige Blüten hervor. Der Rest wird einfarbig blühen. Je drei dieser Tulpenzwiebeln werden in Tüten verpackt.
Ein Kunde kauft im Gartenmarkt ein und erhält eine solche Tüte gratis.
Der Verkäufer sagt: „Es ist genauso wahrscheinlich, drei einfarbige Tulpen zu erhalten wie genau eine zweifarbige Tulpe.“
Stimmt das? Begründe deine Entscheidung.

(3 BE)

Dargestellt ist ein rechteckiger Teil des Geländes des Gartenmarktes. Im Inneren der gepflasterten Fläche wurde ein Teich angelegt, dessen Rand aus aneinandergesetzten Halbkreisen besteht.

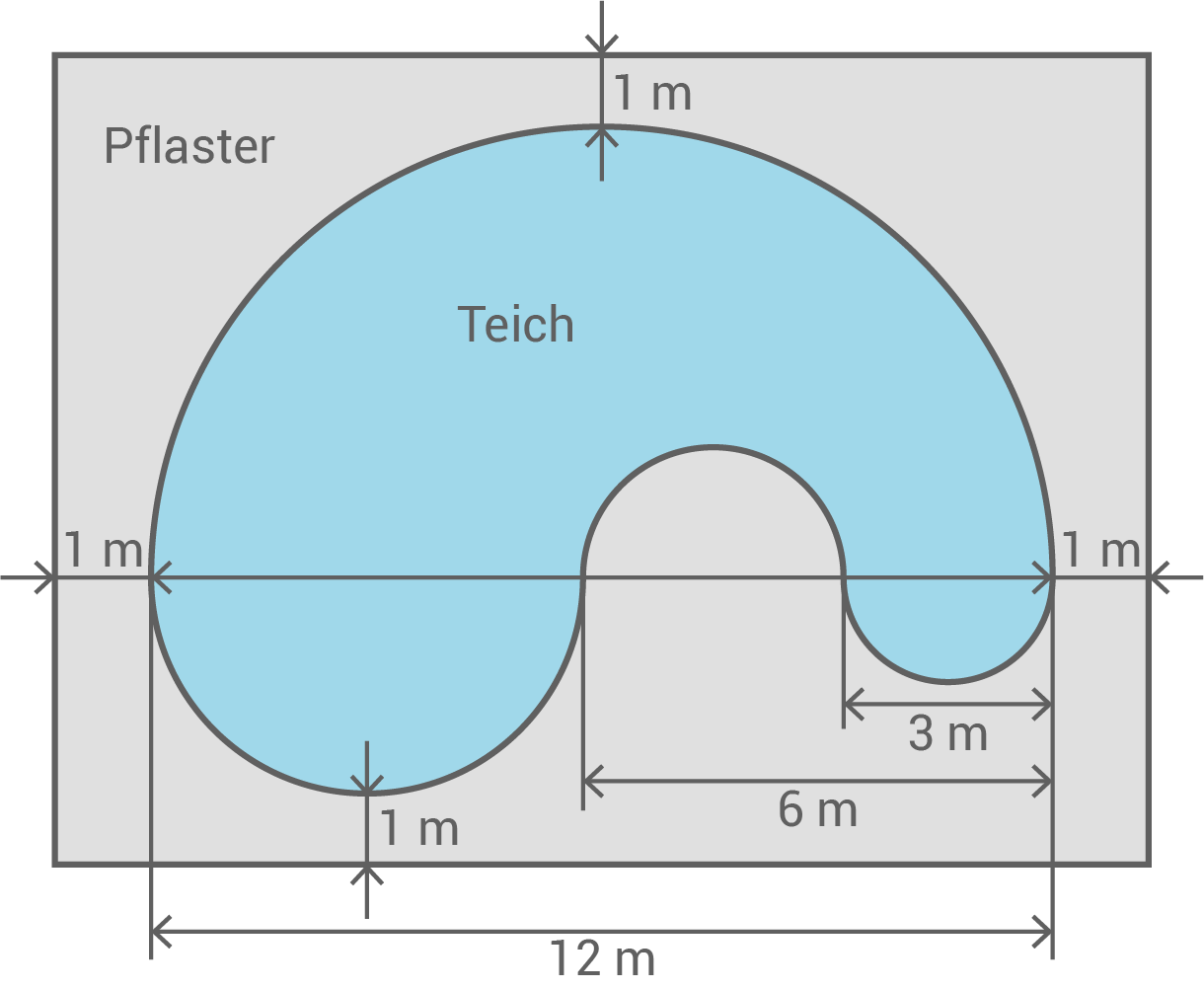
Skizze nicht maßstäblich

Berechne den Flächeninhalt der gepflasterten Fläche.

(3 BE)

Zeige, dass der Umfang der Teichfläche gleich dem Umfang einer Kreisfläche mit dem Radius $r = 6\,\text{m}$ ist.

(3 BE)

Gesamter Umsatz für die Jahre 2013 bis 2015:

$\begin{array}[t]{rll} U&=& 1\,540\,000\, €+2\,100\,000 \,€+2\,860\,000 \,€ \\[5pt] &=& 6\,500\,000 € \end{array}$

10 % davon wurden als Gewinn erwirtschaftet, das entspricht 650 000 €.

Umsatz in den Jahren 2016 und 2020 berechnen

Zunächst muss die Funktionsgleichung von $q$ aufgestellt werden. Es gelten folgende Bedingungen:

$\begin{array}{} \text{I}\quad& q(1)&=& 1,54&=& a+b+c \\ \text{II}\quad& q(2)&=& 2,10&=& 4\cdot a+2\cdot b+c \\ \text{III}\quad& q(3)&=& 2,86&=& 9\cdot a+3\cdot b+c\\ \end{array}$

Der Taschenrechner liefert als Lösung des Gleichungssystems $a=0,1,$ $b=0,26$ und $c=1,18.$ Die Funktionsgleichung von $q$ lautet also $q(x)=0,1x^2+0,26x+1,18.$

Die erwarteten Umsätze für die Jahre 2016 $(q=4)$ und 2020 $(q=8)$ können nun wie folgt berechnet werden:

$q(4)=0,1\cdot4^2+0,26\cdot4+1,18=3,82$

$q(8)=0,1\cdot8^2+0,26\cdot8+1,18=9,66$

Nach der Formel $q$ liegt der erwartete Umsatz für 2016 bei 3,82 Millionen € und für das Jahr 2020 bei 9,66 Millionen €.

Prognose beurteilen

Die Prognose mithilfe der Funktion $q$ erscheint weniger sinnvoll. Für große $x,$ also langfristige Prognosen, wird mit einer zu großen Zunahme gerechnet.

Ereignisse anzeigen

$P(E)=\dfrac{3}{4}$

$P(Z) =\dfrac{1}{4}$

Um die Aussage beurteilen zu können, müssen die Wahrscheinlichkeiten für die betreffenden Ereignisse berechnet werden.

Wahrscheinlichkeit für eine Tüte mit drei einfarbigen Tulpen:

$P(EEE)=\left(\dfrac{3}{4}\right)^3 =\dfrac{27}{64}$

Wahrscheinlichkeit für eine Tüte mit genau einer einfarbigen Tulpe:

Rechenweg anzeigen

$P(ZEE, EZE,EEZ)=\dfrac{27}{64}$

Die beiden Ereignisse sind gleich wahrscheinlich, der Verkäufer hat also recht.

Um den Flächeninhalt der gepflasterten Fläche zu berechnen, wird der Flächeninhalt der gesamten rechteckigen Fläche berechnet und davon der Flächeninhalt der Teichfläche abgezogen.

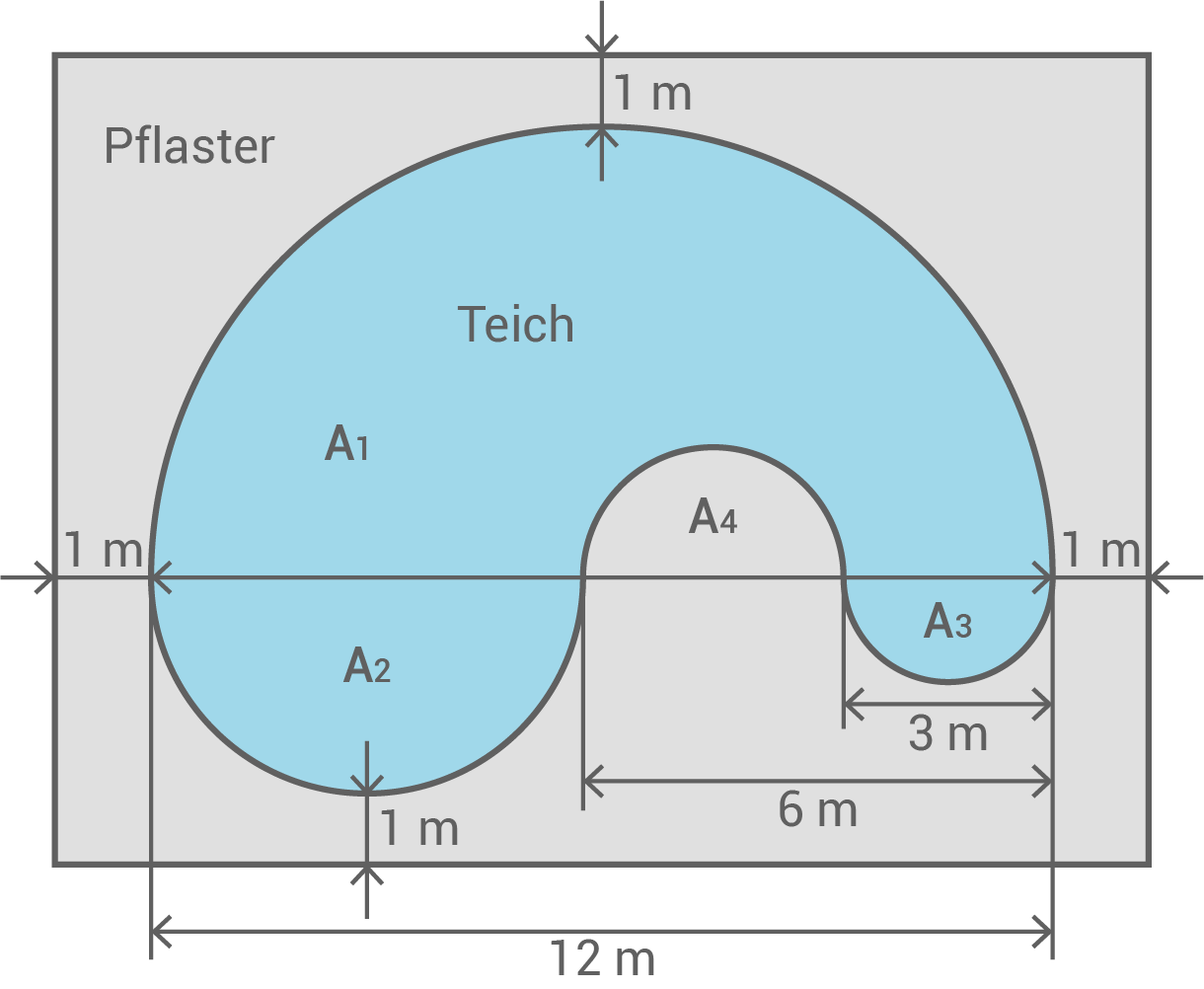Flächeninhalt der Teichfläche berechnen

In der Skizze ist erkennbar, dass die Flächen $A_3$ und $A_4$ gleich groß sind. Wird $A_3$ in $A_4$ eingesetzt, so besteht der Flächeninhalt $A_T$ der Teichfläche nur noch aus den zwei Halbkreisflächen $A_1$ und $A_2.$

$\begin{array}[t]{rll} A_1&=& \dfrac{1}{2}\cdot \pi\cdot (6\,\text{m})^2 \\[5pt] &=& 18\pi \,\text{m}^2 \end{array}$

$\begin{array}[t]{rll} A_2&=& \dfrac{1}{2}\cdot \pi\cdot (3\,\text{m})^2 \\[5pt] &=& 4,5\pi \,\text{m}^2 \end{array}$

Damit folgt insgesamt für den Flächeninhalt der Teichfläche:

$\begin{array}[t]{rll} A_T&=& A_1+A_2 \\[5pt] &=& 18\pi \,\text{m}^2+4,5\pi \,\text{m}^2 \\[5pt] &\approx& 70,7\,\text{m}^2 \end{array}$

Flächeninhalt der rechteckigen Fläche berechnen

Rechenweg anzeigen

$A_R=154\,\text{m}^2$

Flächeninhalt der gepflasterten Fläche berechnen

$\begin{array}[t]{rll} A_P&=& A_R-A_T \\[5pt] &\approx& 154\,\text{m}^2-70,7\,\text{m}^2 \\[5pt] &=& 83,3\,\text{m}^2 \end{array}$

Die gepflasterte Fläche hat einen Flächeninhalt von $83,3\,\text{m}^2.$

Umfang einer Kreisfläche mit Radius r = 6 m berechnen

$u=2\pi r=2\pi\cdot 6\,\text{m}=12\pi \,\text{m}$

Umfang der Teichfläche berechnen

$u_1=\pi\cdot 6\,\text{m}$
$u_2=\pi\cdot 3\,\text{m}$
$u_3=u_4=\pi\cdot 1,5\,\text{m}$

Rechenweg anzeigen

$\begin{array}[t]{rll} u_T&=& u_1+u_2+u_3+u_4 \\[5pt] &=& 12\pi \,\text{m} \end{array}$

Die beiden Umfänge stimmen also überein.