Wahlaufgaben

Wahlaufgabe 1 mit Schwerpunkt Arithmetik/Algebra

Frau Glück gewinnt $50\,000$ Euro im Lotto, die sie als Festgeld für $20$ Jahre anlegen möchte. Dazu prüft sie Angebote von zwei Banken. Bank A bietet ihr einen festen Jahreszinssatz von $2,5\,\%$ an. Bank B verspricht bei ebenfalls festem Jahreszins, dass sich ihr Kapital innerhalb der nächsten $15$ Jahre auf $75\,000$ Euro erhöht hat.

Berechne jeweils das Kapital nach $20$ Jahren.
Vergleiche beide Angebote.

(5 BE)

Wahlaufgabe 2 mit Schwerpunkt Funktion

Gegeben ist die Funktion $f$ durch $f(x)=(x+2)^{\frac{1}{2}}\quad$ $(x \in \mathbb{R};\:x\geq-2).$

Gib die Schnittpunkte des Graphen mit den Koordinatenachsen an.

(2 BE)

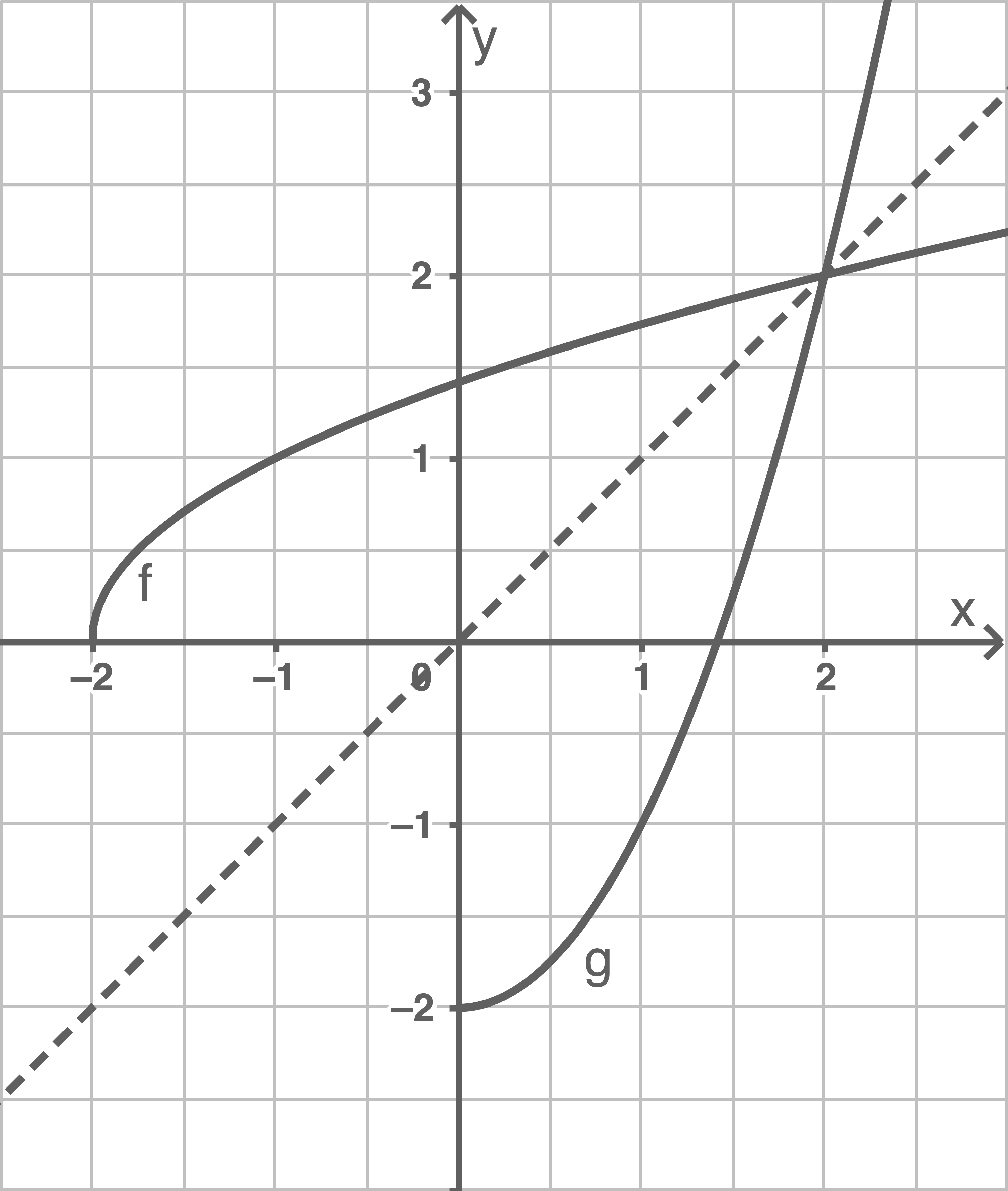
Zeichne den Graphen von $f$ und den Graphen der zugehörigen Umkehrfunktion in ein und dasselbe Koordinatensystem.

(3 BE)

Wahlaufgabe 3 mit Schwerpunkt Geometrie

Die Grundfläche eines Swimmingpools hat die Form eines Rechtecks mit zwei angesetzten Halbkreisen (siehe Skizze).

Skizze nicht maßstäblich

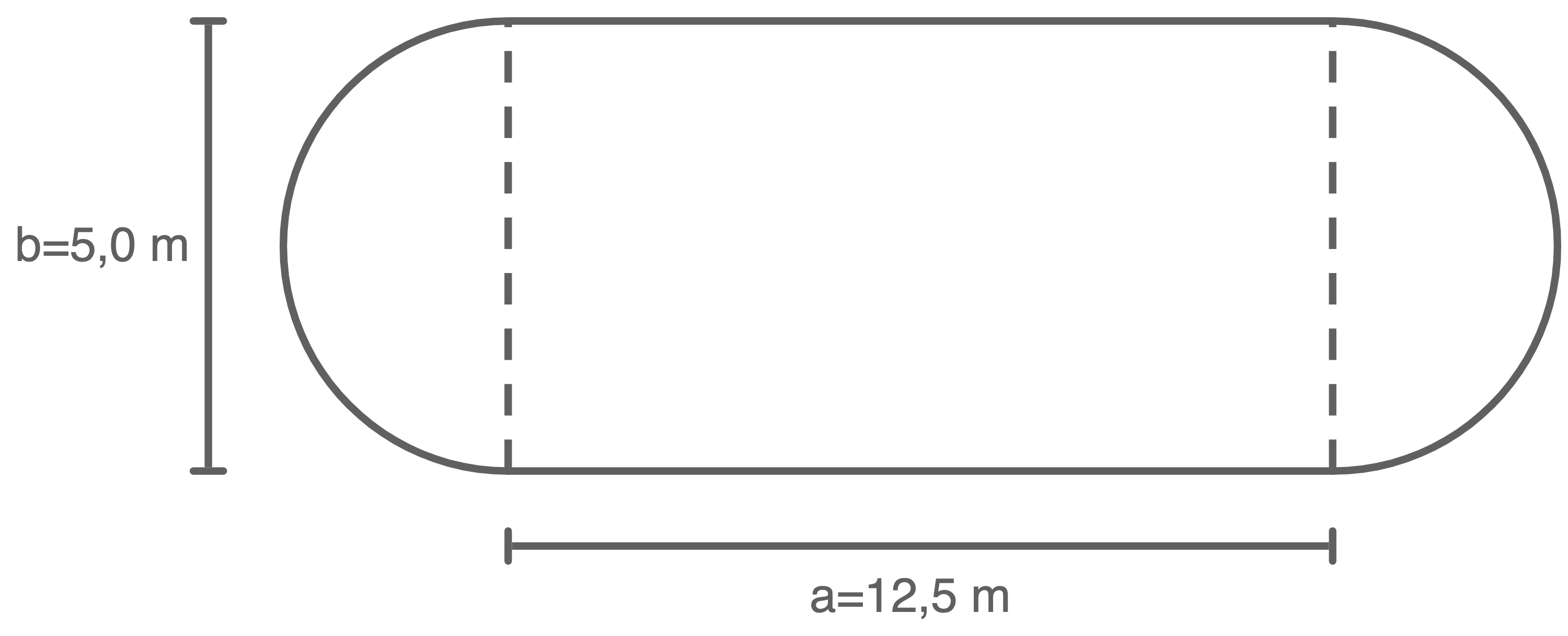
Berechne den Flächeninhalt der Grundfläche des Pools.
Begründe, dass das Volumen des Swimmingpools mit der Tiefe $t$ durch die Formel $V=a \cdot b \cdot t+\pi \cdot\big(\tfrac{b}{2}\big)^2 \cdot t$ berechnet werden kann.

(3 BE)

In den Swimmingpool passen $150 \mathrm{~m}^3$ Wasser. In einer Stunde können $18\,000$ Liter Wasser in den Pool gepumpt werden. Um 08:00 Uhr ist der Pool leer und die Pumpe wird eingeschaltet.

Ermittle den frühesten Zeitpunkt, an dem der Pool vollständig gefüllt ist.

(2 BE)

Wahlaufgabe 4 mit Schwerpunkt Geometrie

Die Geraden $g$ und $h$ haben den gemeinsamen Punkt $Z$ und werden von den drei parallelen Geraden $i,\:j$ und $k$ geschnitten, so dass die in der Skizze dargestellte Figur entsteht.

Bekannt sind die Längen der Strecken $\overline{DE}=7,5\,\text{cm},$ $\overline{AD}=18,0\,\text{cm}$ und $\overline{BE}=23,4\,\text{cm}.$

Skizze nicht maßstäblich

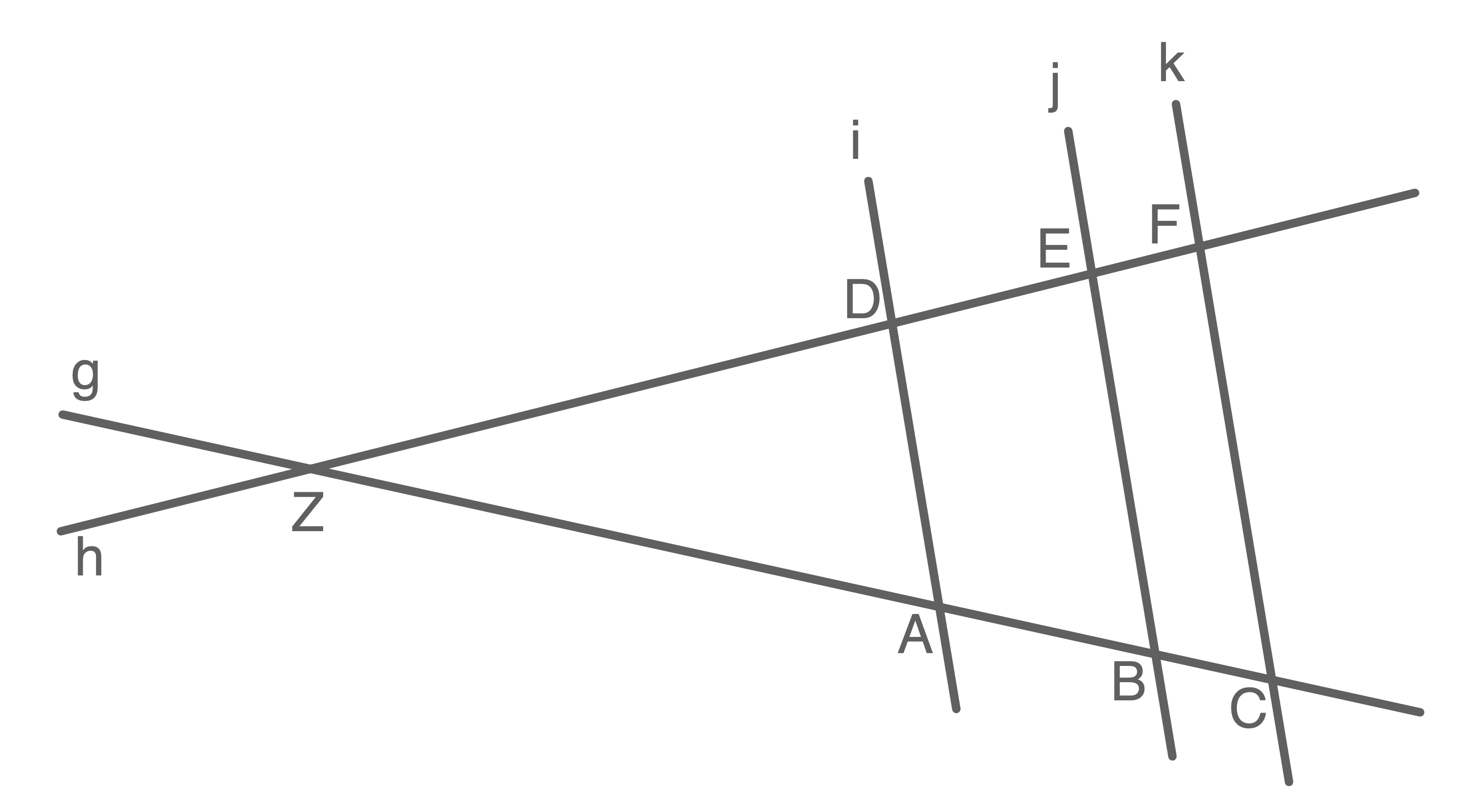
Weise rechnerisch nach, dass die Strecke $\overline{ZD}$ eine Länge von $25\,\text{cm}$ besitzt.

(2 BE)

Der Flächeninhalt des Dreiecks $ZCF$ ist dreimal so groß wie der Flächeninhalt des Dreiecks $ZAD.$

Berechne die Länge der Strecke $\overline{EF}.$

(3 BE)

Wahlaufgabe 5 mit Schwerpunkt Stochastik

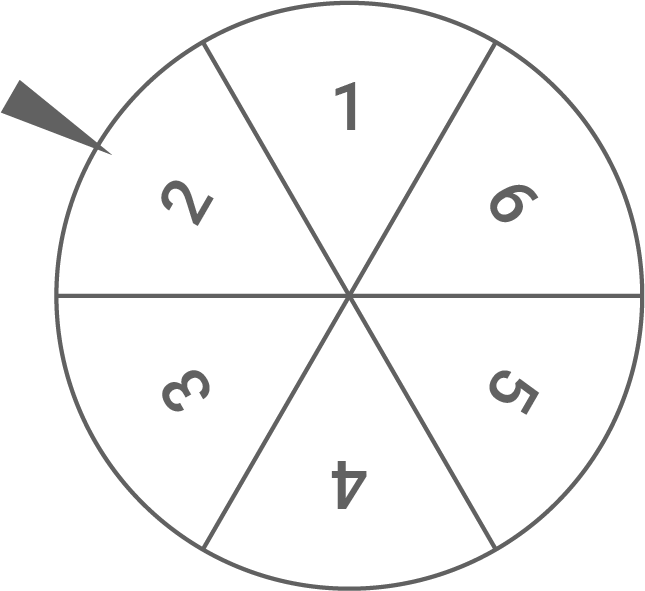
Bei einem Spiel darf Luca das Glücksrad zweimal drehen (siehe Skizze).
Wenn nur gerade Zahlen gedreht werden, bekommt Luca $2\,\text{€}$ ausgezahlt. Beträgt die Summe der beiden gedrehten Zahlen sieben, muss Luca $3\,\text{€}$ bezahlen. In allen anderen Fällen erhält er nichts und muss auch nichts bezahlen.

Untersuche, ob es sich hierbei um ein faires Spiel handelt.
(Hinweis: Ein Spiel heißt fair, wenn der Erwartungswert des Gewinns null ist.)

(5 BE)

Wahlaufgabe 6 mit Schwerpunkt Stochastik

Beim einmaligen Werfen eines gezinkten Würfels fällt die „Sechs“ mit der Wahrscheinlichkeit $p.$ Dieser Würfel wird genau zweimal geworfen.

Stelle diesen Sachverhalt in einem vollständig beschrifteten Baumdiagramm dar.

(2 BE)

Die Wahrscheinlichkeit dafür, dass beim zweimaligen Werfen genau einmal die „Sechs“ fällt, beträgt $45,5\,\%.$

Berechne die beiden möglichen Werte für die Wahrscheinlichkeit $p.$

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Wahlaufgabe 1 mit Schwerpunkt Arithmetik/Algebra

Bank A:
$K_{20}=50000\,\text{€}\cdot 1,025^{20}\approx 81930,82\,\text{€}$

Bank B:
$\begin{array}[t]{rlll} 50000\cdot b^{15}&=&75000 &\mid\;:50000 \\[5pt] b^{15}&=&1,5&\mid\;\sqrt[15]{1,5}\\[5pt] b&\approx&1,027 \end{array}$

$K_{20}=50000\,\text{€}\cdot 1,027^{20}\approx 85188,09\,\text{€}$

Vergleichen: Das Angebot der Bank B ist vorteilhafter.

Wahlaufgabe 2 mit Schwerpunkt Funktion

Schnittpunkt mit der $\boldsymbol{x}$ -Achse bestimmen

$\begin{array}[t]{rlll} (x+2)^{\frac{1}{2}}&=&0 &\mid\; \left(\right)^2\\[5pt] x+2&=&0\\[5pt] x&=&-2 \end{array}$

$P_x(-2\mid 0)$

Schnittpunkt mit der $\boldsymbol{y}$ -Achse bestimmen

$\begin{array}[t]{rlll} f(0)&=&\left(0+2\right)^{\frac{1}{2}}\\[5pt] f(0)&=&\sqrt{2} \end{array}$

$P_y\bigl(0\mid \sqrt{2}\bigr)$

Umkehrfunktion $\boldsymbol{g(x)}$ bilden

$\begin{array}[t]{rlll} y&=&(x+2)^{\frac{1}{2}} &\mid\:x\text{ und } y \text{ vertauschen}\\[5pt] x&=&(y+2)^{\frac{1}{2}}&\mid\:()^2\\[5pt] x^2&=&y+2&\mid\:-2\\[5pt] x^2-2&=&y \end{array}$

Somit gilt für die Umkehrfunktion:

$g(x)=x^2-2$

Da der Wertebereich für $f(x)$ nur die reellen Zahlen größer gleich $0$ umfasst, gilt für den Definitionsbereich von $g(x),$ dass dieser nur reelle Zahlen größer gleich $0$ beinhaltet.

Wahlaufgabe 3 mit Schwerpunkt Geometrie

$\begin{array}[t]{rlll} A&=&5\,\text{m}\cdot 12,5\,\text{m}+\pi\cdot (2,5\,\text{m})^2 \\[5pt] &\approx&82,1\,\text{m}^2 \end{array}$

Begründen:
Der erste Teil der Formel entspricht dem Volumen eines Quaders $V_Q=a\cdot b\cdot t$ und der zweite Teile dem Volumen eines Zylinders $V_Z=\pi\cdot \bigl(\tfrac{b}{2}\bigr)^2\cdot t.$

$1\,\text{m}^3$ entspricht $1\,000\,\text{dm}^3,$ was $1\,000$ Litern entspricht. In den Pool passen folglich $150\,000$ Liter.

$150\,000\;\text{L}:18\,000\,\dfrac{\text{L}}{\text{h}}= 8\dfrac{1}{3}\,\text{h}$

$8\tfrac{1}{3}\,\text{h}$ entsprechen $8$ Stunden und $20$ Minuten. Frühestens um 16:20 Uhr ist der Pool also vollständig gefüllt.

Wahlaufgabe 4 mit Schwerpunkt Geometrie

Rechenweg anzeigen

$\overline{ZD}=25\,\text{cm}$

Wegen $A(ZCF)=3\cdot A(ZAD)$ gilt:

$\dfrac{A(ZCF)}{A(ZAD)}=\dfrac{3\cdot A(ZAD)}{A(ZAD)}=3$

$A_{\text{groß}}=k^2\cdot A_{\text{klein}}$

$k=\dfrac{\overline{ZF}}{\overline{ZD}}$

$\begin{array}[t]{rlll} \left(\dfrac{\overline{ZF}}{\overline{ZD}}\right)^2&=&3 &\mid\;\sqrt{\,\,} \\[5pt] \dfrac{\overline{ZF}}{\overline{ZD}}&=&\sqrt{3}\\[5pt] \end{array}$

Weil eine Streckenlänge nur positiv sein kann, ist nur $+\sqrt{3}$ eine Lösung.

$\begin{array}[t]{rlll} \dfrac{\overline{ZF}}{\overline{ZD}}&=&\sqrt{3} &\mid\;\cdot \overline{ZD} \\[5pt] \overline{ZF}&=&\sqrt{3}\cdot \overline{ZD}\\[5pt] \overline{ZF}&=&\sqrt{3}\cdot 25\,\text{cm}\\[5pt] \overline{ZF}&\approx&43,3\,\text{cm} \end{array}$

Damit ergibt sich:

$\begin{array}[t]{rlll} \overline{EF}&=&\overline{ZF}-\overline{ZD}-\overline{DE}\\[5pt] \overline{EF}&=&43,3\,\text{cm}-25\,\text{cm}-7,5\,\text{cm}\\[5pt] \overline{EF}&=&10,8\,\text{cm} \end{array}$

Wahlaufgabe 5 mit Schwerpunkt Stochastik

Nur gerade Zahlen:

$P(E_1)=\dfrac{3}{6}\cdot \dfrac{3}{6}=\dfrac{1}{4}=25\,\%$

Summe $7$ :

$P(E_2)=6\cdot \dfrac{1}{6}\cdot \dfrac{1}{6}=\dfrac{1}{6}\approx 16,7\,\%$

$E(X)=\dfrac{1}{4}\cdot 2\,\text{€}+\dfrac{1}{6}\cdot (-3\,\text{€})=0$

Das Spiel ist fair.

Wahlaufgabe 6 mit Schwerpunkt Stochastik

$\begin{array}[t]{rlll} 2\cdot p\cdot (1-p)&=&0,455\\[5pt] 2p-2p^2&=&0,455 &\mid\;:(-2) \\[5pt] -p+p^2&=&-0,2275 &\mid\;+0,2275 \\[5pt] p^2-p+0,2275&=&0 \\[5pt] \end{array}$

$\begin{array}[t]{rlll} p_{1,2}&=& -\dfrac{p^*}{2} \pm \sqrt{\left(\dfrac{p^*}{2}\right)^2-q} \\[5pt] p_{1,2}&=& -\dfrac{-1}{2} \pm \sqrt{\left(\dfrac{-1}{2}\right)^2-0,2275} \\[5pt] p_{1,2}&=& \dfrac{1}{2} \pm 0,15 \end{array}$

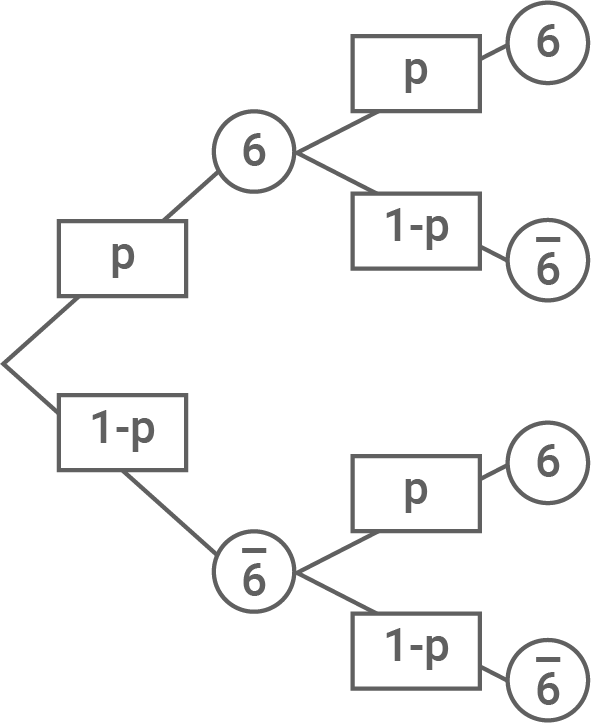
Damit folgt für die Wahrscheinlichkeit:

$\begin{array}[t]{rlll}p_1&=&0,65 \\[5pt] p_2&=&0,35 \\[5pt] \end{array}$

Die Wahrscheinlichkeit, dass beim gezinkten Würfel eine, „Sechs“ fällt, beträgt entweder $65\,\%$ oder $35\,\%.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?