Wahlaufgabe 1
1.
Im Jahr 1922 wurde vom Deutschen Institut für Normung (DIN) festgelegt, dass das Seitenverhältnis von Breite und Länge eines Papierbogens im A-Format  sein muss.
sein muss.
Ein Papierbogen im Format A0 hat einen Flächeninhalt von einem Quadratmeter.
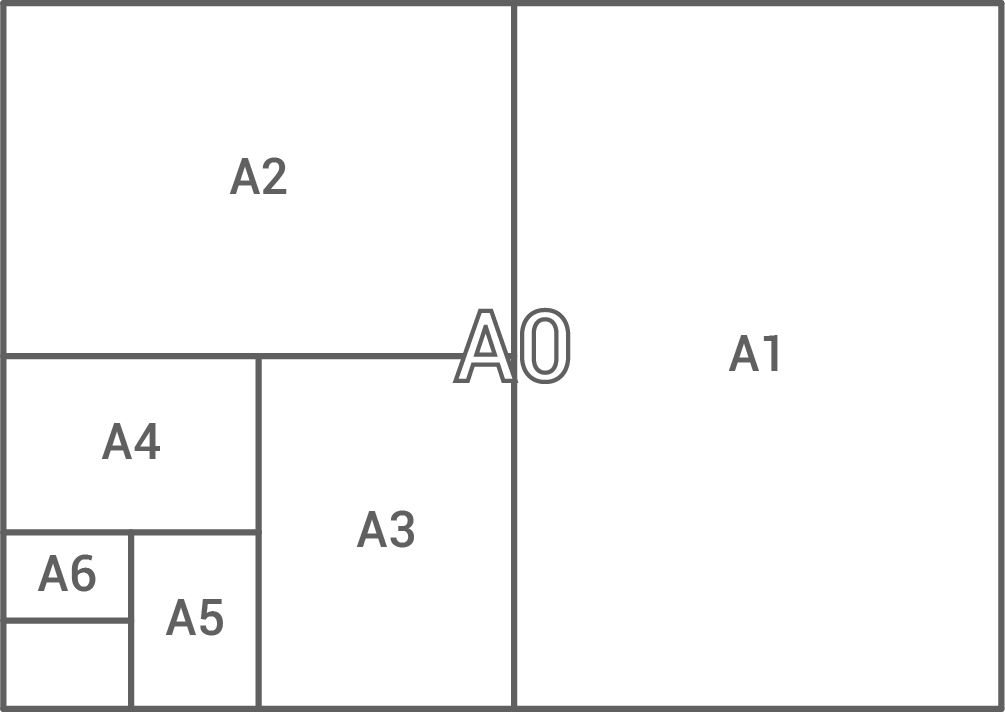
Ein Papierbogen im Format A0 hat einen Flächeninhalt von einem Quadratmeter.

a)
Berechne die Seitenlängen eines A0-Papierbogens auf Millimeter genau.
(3 BE)
b)
Daniela behauptet, dass bei jedem Papierbogen der A-Formate für die kurze Seite  und die Diagonale
und die Diagonale  gilt:
gilt:

Untersuche, ob diese Aussage wahr ist.
Untersuche, ob diese Aussage wahr ist.
(3 BE)
c)
Vergrößert man ein A4-Format auf ein A2-Format, muss man am Kopierer den Vergrößerungsfaktor 200 % wählen.
Daniela kopiert ein Quadrat mit der Seitelänge und wählt am Kopierer einen Faktor von 50 %.
und wählt am Kopierer einen Faktor von 50 %.
Beschreibe den Einfluss dieses Faktors auf die Seitenlänge und den Flächeninhalt der Kopie des Quadrats im Vergleich zum Original.
Daniela kopiert ein Quadrat mit der Seitelänge
Beschreibe den Einfluss dieses Faktors auf die Seitenlänge und den Flächeninhalt der Kopie des Quadrats im Vergleich zum Original.
(2 BE)
2.
Zwei Biologiestudenten benötigen für ihre Untersuchungen eine große Anzahl an Zellen.
Ein Student arbeitet mit Zelltyp I. Er hat zu Beginn nur eine Zelle. Bei diesem Zelltyp teilt sich jede Zelle innerhalb einer halben Stunde in zwei Zellen dieses Zelltyps.
Ein Student arbeitet mit Zelltyp I. Er hat zu Beginn nur eine Zelle. Bei diesem Zelltyp teilt sich jede Zelle innerhalb einer halben Stunde in zwei Zellen dieses Zelltyps.
a)
Ermittle eine Funktionsgleichung, die die Anzahl der Zellen in Abhängigkeit von der Zeit beschreibt.
Bestimme die Zeit, nach der der Student mindestens 50 000 Zellen zur Verfügung hat.
Eine Studentin führt Untersuchungen am Zelltyp II durch. Sie beginnt 08:00 Uhr mit genau zehn Zellen. 13:00 Uhr sind es 320 Zellen. Das Labor schließt 20:00 Uhr.
Bestimme die Zeit, nach der der Student mindestens 50 000 Zellen zur Verfügung hat.
(3 BE)
b)
Untersuche, ob die Studentin bis zur Schließung des Labors mindestens 50 000 Zellen zur Verfügung hat.
(4 BE)
3.
In einem Betrieb werden Gläser mit Deckel hergestellt.
Es ist bekannt, dass 3 % der Gläser und 2 % der Deckel fehlerhaft sind. Zur Kontrolle werden jeweils zufällig ein Glas und ein Deckel entnommen.
Es ist bekannt, dass 3 % der Gläser und 2 % der Deckel fehlerhaft sind. Zur Kontrolle werden jeweils zufällig ein Glas und ein Deckel entnommen.
a)
Berechne die Wahrscheinlichkeiten folgender Ereignisse:
 „Glas und Deckel sind fehlerfrei.“
„Glas und Deckel sind fehlerfrei.“
 „Entweder das Glas oder der Deckel ist fehlerhaft.“
„Entweder das Glas oder der Deckel ist fehlerhaft.“
(3 BE)
b)
Beurteile, ob mit einem der Ereignisse  und
und  das Gegenereignis zu
das Gegenereignis zu  (siehe Teilaufgabe a) beschrieben wird.
(siehe Teilaufgabe a) beschrieben wird.
 „Glas und Deckel sind fehlerhaft.“
„Glas und Deckel sind fehlerhaft.“
 „Glas oder Deckel sind fehlerhaft.“
„Glas oder Deckel sind fehlerhaft.“
(2 BE)
1.
a)
Die kürzere Seite des Rechtecks wird mit  bezeichnet. Dann gilt
bezeichnet. Dann gilt  und damit gilt für die längere Seite
und damit gilt für die längere Seite  Der Flächeninhalt eines Rechtecks lässt sich mit der Formel
Der Flächeninhalt eines Rechtecks lässt sich mit der Formel  berechnen. Der A0-Bogen hat einen Flächeninhalt von
berechnen. Der A0-Bogen hat einen Flächeninhalt von  Gesucht sind also Werte für
Gesucht sind also Werte für  und
und  die die Gleichung
die die Gleichung  erfüllen.
erfüllen.
![\(\begin{array}[t]{rll}
10^6\,\text{mm}^2&=& a\cdot b \\[5pt]
10^6\,\text{mm}^2&=& \sqrt{2}b\cdot b \quad \scriptsize \mid\; :\sqrt{2} \\[5pt]
\dfrac{10^6\,\text{mm}^2}{\sqrt{2}}&=& b^2 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
841\,\text{mm}&\approx& b
\end{array}\)](https://www.schullv.de/resources/formulas/fbf236779aa4907aebfc73df43d15c01c8154e4d2a96b1dc347eabae5066dcc2_light.svg) Damit folgt
Damit folgt  Die Seiten eines A0-Bogens sind 841 mm und 1 189 mm lang.
Die Seiten eines A0-Bogens sind 841 mm und 1 189 mm lang.
b)
Nach Teilaufgabe a) gilt 
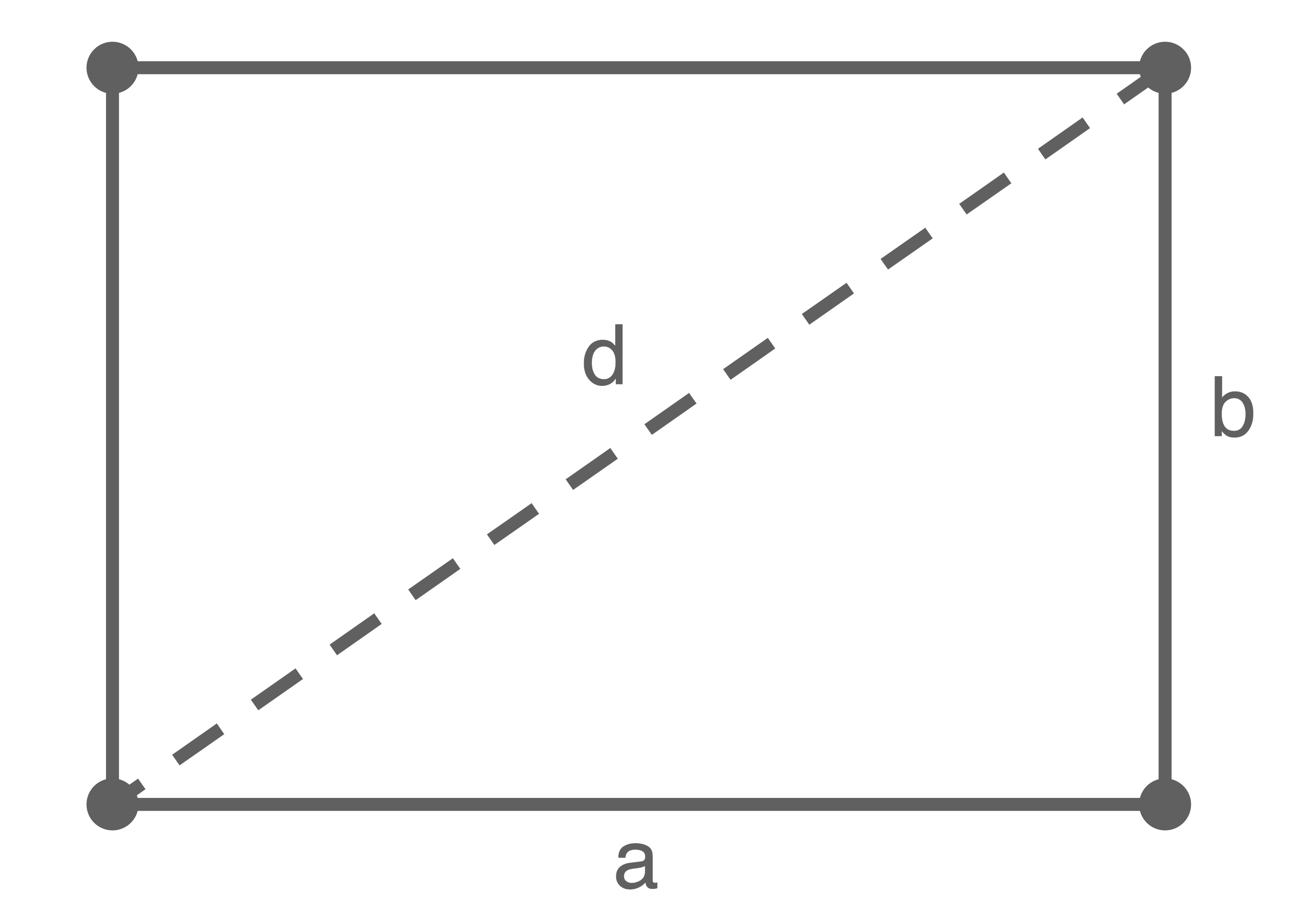 Mit dem Satz des Pythagoras folgt:
Mit dem Satz des Pythagoras folgt:
![\(\begin{array}[t]{rll}
d^2&=& a^2+b^2 \\[5pt]
d^2&=& (\sqrt{2}b)^2+b^2 \\[5pt]
d^2&=& 3b^2 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
d&=& \sqrt{3}b \quad \scriptsize \mid\; :b \\[5pt]
\dfrac{d}{b}&=& \sqrt{3} \quad \scriptsize \mid\; ()^{-1} \\[5pt]
\dfrac{b}{d}&=&\dfrac{1}{\sqrt{3}}
\end{array}\)](https://www.schullv.de/resources/formulas/90a97c0142a18cfb0a112e91b6e99bc4c90ae4e1d49683e5673aed307ab7cddf_light.svg) Die Aussage ist wahr.
Die Aussage ist wahr.

c)
Der Abbildung kann entnommen werden, dass bei einer Vergrößerung um 200 % von A4 auf A2 die Seitenlängen verdoppelt und dier Flächeninhalt vervierfacht wird.
Analog muss es bei einer Kopie mit dem Faktor 50 % zu einer Halbierung der Seitenlängen kommen. Für den Flächeninhalt des Quadrats gilt dann:
 Der Flächeninhalt der Kopie sinkt im Vergleich zum Original also auf ein Viertel.
Der Flächeninhalt der Kopie sinkt im Vergleich zum Original also auf ein Viertel.
2.
a)
Funktionsgleichung ermitteln
Gesucht ist eine Exponentialfunktion der Form  Dabei gibt
Dabei gibt  den Anfangsbestand der Zellen. Da sich jede Zelle innerhalb einer halben Stunde in zwei Zellen aufteilt, gibt
den Anfangsbestand der Zellen. Da sich jede Zelle innerhalb einer halben Stunde in zwei Zellen aufteilt, gibt  den Wachstumsfakor für eine Stunde an. Es ergibt sich also folgende Funktionsgleichung:
den Wachstumsfakor für eine Stunde an. Es ergibt sich also folgende Funktionsgleichung:
 Dabei gibt
Dabei gibt  die Zeit nach Versuchsbeginn in Stunden und
die Zeit nach Versuchsbeginn in Stunden und  die Anzahl der Zellen an.
Zeit bestimmen
Gesucht ist die Lösung der Gleichung
die Anzahl der Zellen an.
Zeit bestimmen
Gesucht ist die Lösung der Gleichung 
![\(\begin{array}[t]{rll}
f(x)&=& 50\,000 \\[5pt]
4^x&=& 50\,000 \quad \scriptsize \mid\; \lg \\[5pt]
x\cdot \lg(4)&=& \lg(50\,000) \quad \scriptsize \mid\; :\lg(4) \\[5pt]
x&=& \dfrac{\lg(50\,000)}{\lg(4)} \\[5pt]
x&\approx& 7,8
\end{array}\)](https://www.schullv.de/resources/formulas/9eb77549aaf25a3a82dca29a86766c671a2bcd7e31ec0736aeaf1634ac85c244_light.svg) Nach ungefähr 7,8 Stunden hat der Student mindestens 50 000 Zellen zur Verfügung.
Nach ungefähr 7,8 Stunden hat der Student mindestens 50 000 Zellen zur Verfügung.
b)
Gesucht ist wieder eine Exponentialfunktion der Form  Der Anfangsbestand ist durch
Der Anfangsbestand ist durch  gegeben, der Wachstumsfaktor muss berechnet werden. Die Funktionsgleichung ist also von der Form
gegeben, der Wachstumsfaktor muss berechnet werden. Die Funktionsgleichung ist also von der Form  Die Zeitspanne von 8 Uhr bis 13 Uhr beträgt 5 Stunden. Nach dieser Zeit sind 320 Zellen vorhanden, es gilt also
Die Zeitspanne von 8 Uhr bis 13 Uhr beträgt 5 Stunden. Nach dieser Zeit sind 320 Zellen vorhanden, es gilt also  Damit lässt sich der Wachstumsfaktor
Damit lässt sich der Wachstumsfaktor  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
g(5)&=& 320 \\[5pt]
10\cdot b^5&=& 320 \quad \scriptsize \mid\; :10 \\[5pt]
b^5&=& 32 \\[5pt]
b^5&=& 2^5 \\[5pt]
b&=& 2
\end{array}\)](https://www.schullv.de/resources/formulas/a8483c32f175c9979eb0230be244617eb983c8d3576da6902e4f32cedb156800_light.svg) Die Funktion
Die Funktion  ist also gegeben durch
ist also gegeben durch  wobei
wobei  die Zeit nach 8 Uhr in Stunden und
die Zeit nach 8 Uhr in Stunden und  die Anzahl der Zellen angibt.
Von 8 Uhr bis 20 Uhr vergehen 12 Stunden. Es gilt zu überprüfen, ob in dieser Zeit mindestens 50 000 Zellen zur Verfügung stehen.
die Anzahl der Zellen angibt.
Von 8 Uhr bis 20 Uhr vergehen 12 Stunden. Es gilt zu überprüfen, ob in dieser Zeit mindestens 50 000 Zellen zur Verfügung stehen.
 Zur Schließung des Labors sind weniger als 50 000 Zellen vorhanden.
Zur Schließung des Labors sind weniger als 50 000 Zellen vorhanden.
3.
a)
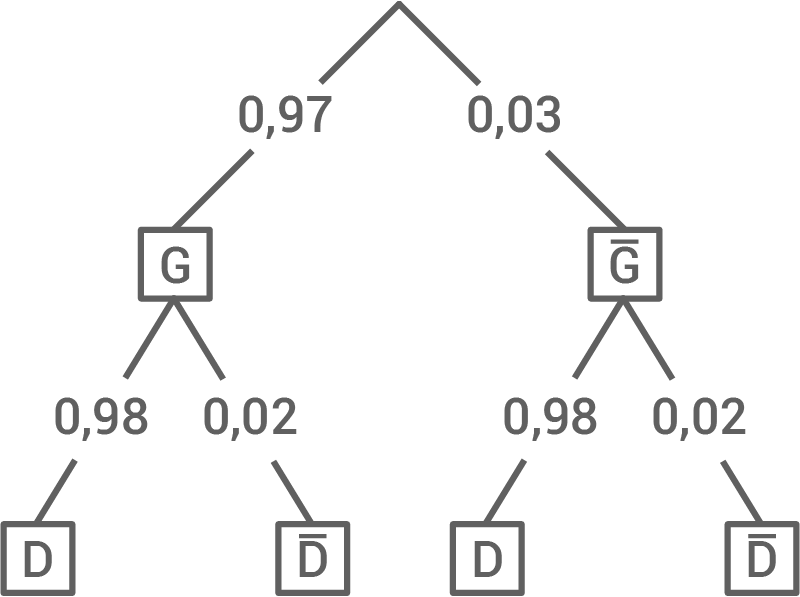
b)
Zum Ereignis  gehört nur das Ergebnis
gehört nur das Ergebnis  Für das Gegenereignis müssen also alle anderen Ergebnisse
Für das Gegenereignis müssen also alle anderen Ergebnisse 
 und
und  gehören.
Zum Ereignis
gehören.
Zum Ereignis  gehört nur das Ergebnis
gehört nur das Ergebnis  es beschreibt also nicht das Gegenereignis von
es beschreibt also nicht das Gegenereignis von  Zum Ereignis
Zum Ereignis  gehören die Ergebnisse
gehören die Ergebnisse 
 und
und  Das Ereignis
Das Ereignis  beschreibt also das Gegenereignis zu
beschreibt also das Gegenereignis zu 