Wahlaufgabe 1

Lukas backt 40 Muffins für eine Klassenfeier. Er füllt 32 Muffins mit Heidelbeeren und die restlichen mit Pudding. Die Füllung ist von außen nicht zu erkennen.

Max hat sich als erster drei Muffins nacheinander genommen.
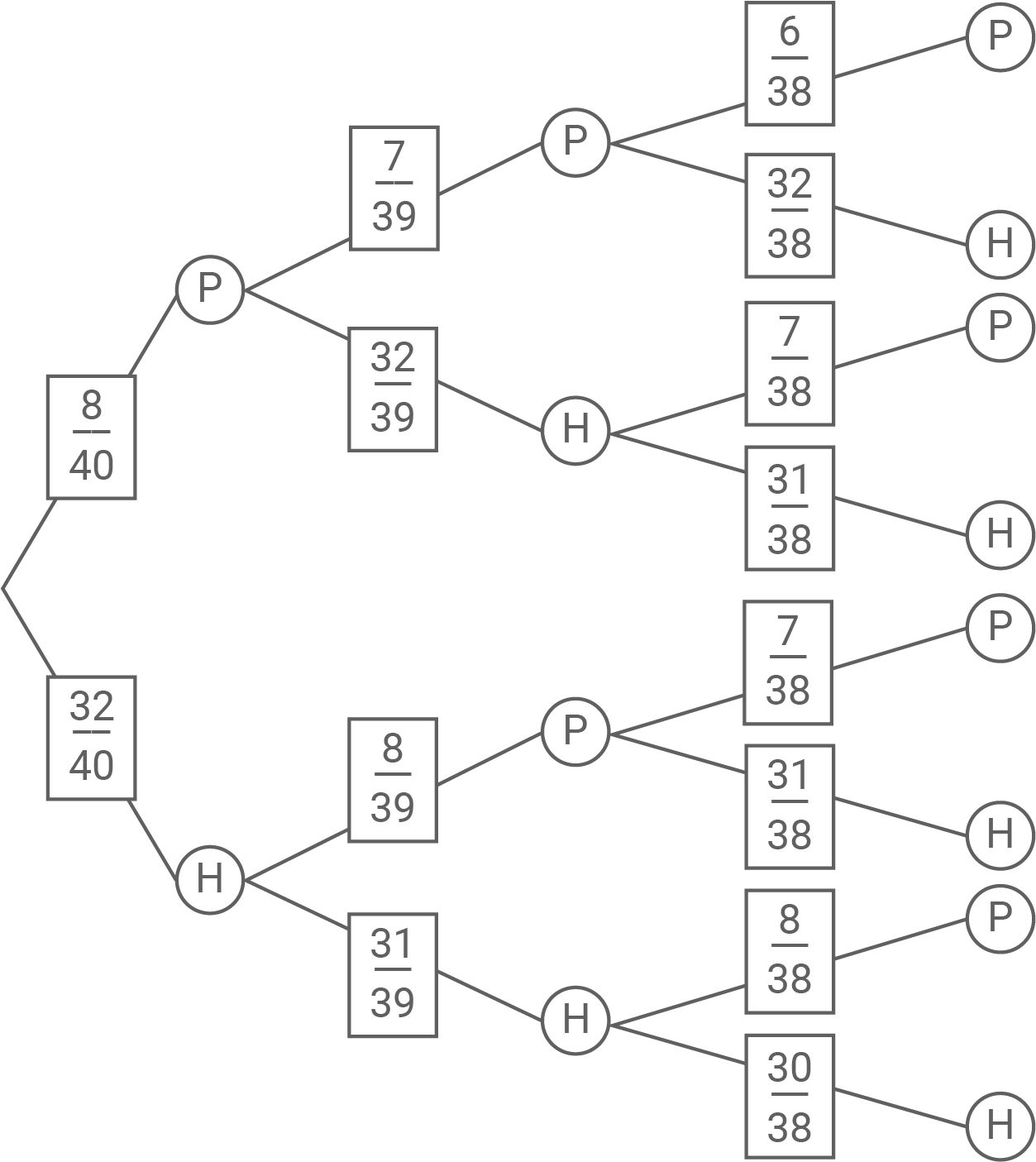
Veranschauliche den Sachverhalt in einem vollständig beschrifteten Baumdiagramm.
Berechne die Wahrscheinlichkeit dafür, dass Max mindestens einen Muffin mit Pudding genommen hat.

(4 BE)

Formuliere die Ereignisse $A$ und $B$ in Worten, deren Wahrscheinlichkeiten durch folgende Gleichungen berechnet werden können.

$\begin{aligned} P(A)&=\frac{8}{40} \cdot \frac{7}{39}+\frac{32}{40} \cdot \frac{31}{39} \\[5 pt] P(B)&=\frac{8}{40} \cdot \frac{7}{39} \cdot \frac{6}{38}+3 \cdot \frac{8}{40} \cdot \frac{7}{39} \cdot \frac{32}{38} \end{aligned}$

(4 BE)

Die Skizze zeigt den Rest eines Aufschriebs zum Thema Schnittpunktberechnung von linearen und quadratischen Funktionen.

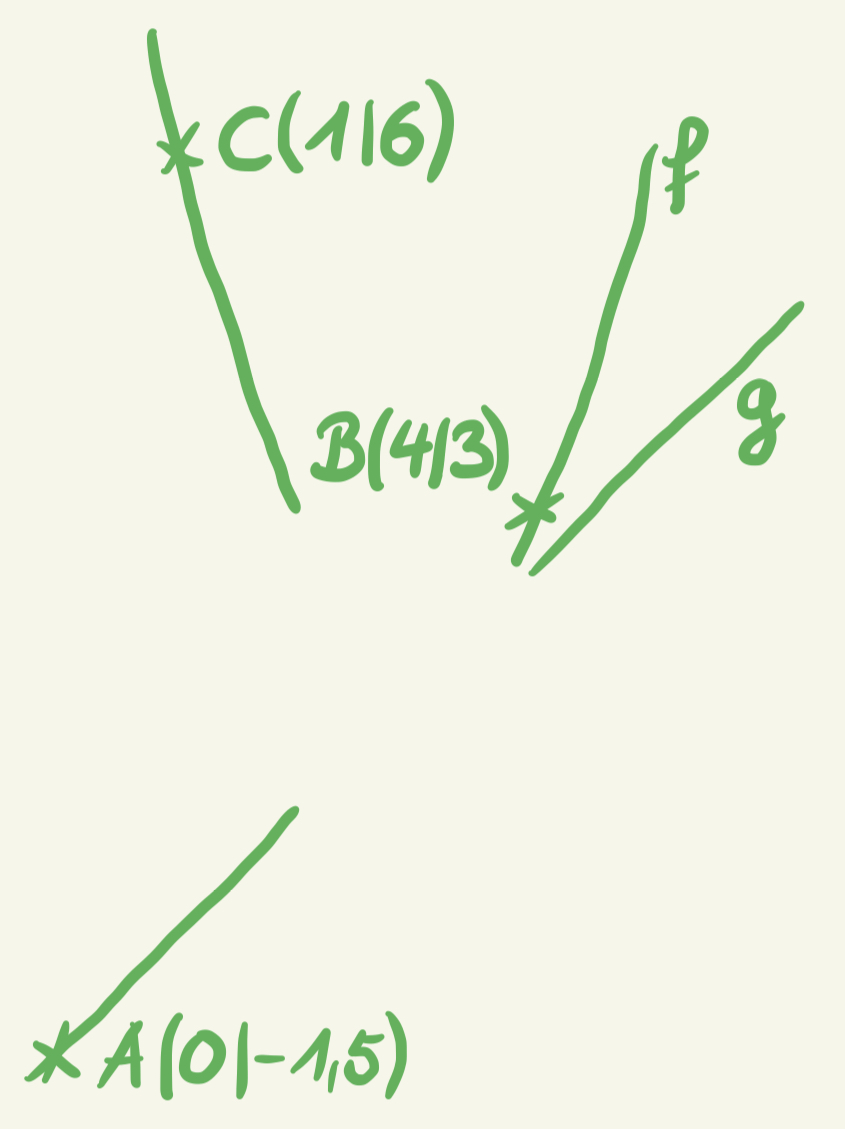
Abbildung nicht maßstäblich

Der Punkt $A$ liegt auf dem Graphen einer linearen Funktion $g$ mit dem Anstieg $m=1.$ Die Punkte $B$ und $C$ sind Punkte einer Parabel zur quadratischen Funktion $f$ mit $f(x)=x^2+p x+q.$
Jule behauptet, dass die Graphen von $f$ und $g$ keinen gemeinsamen Punkt haben.

Untersuche, ob Jules Behauptung richtig ist.

(4 BE)

Die Punkte $A,$ $B$ und $C$ bilden ein Dreieck. Prüfe rechnerisch, ob das Dreieck $A B C$ rechtwinklig ist.

(4 BE)

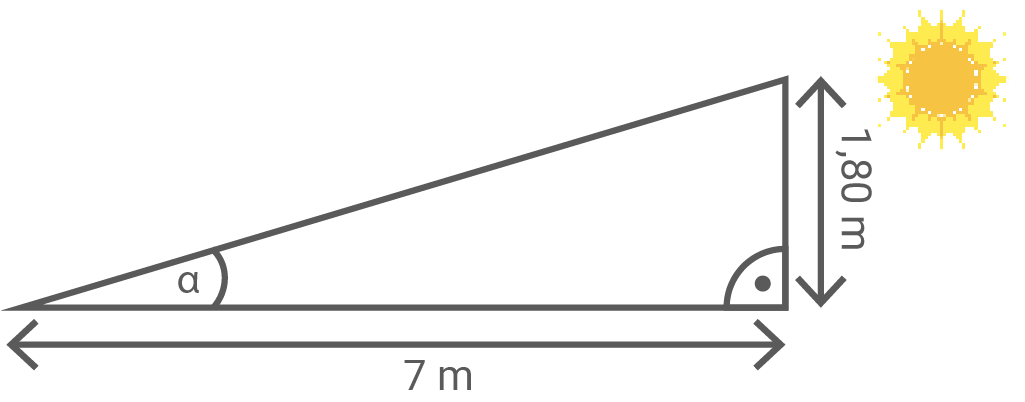
Nico und Nina wollen die Höhe des Ahornbaumes auf dem Schulhof bestimmen. Dazu messen sie Schattenlängen. Die Schattenlänge des Ahornbaumes beträgt $60 \,\text{m}.$ Nico ist $180 \,\text{cm}$ groß und sein Schatten $7 \,\text{m}$ lang.

Berechne die Höhe des Ahornbaums.

2 BE

Berechne die Größe des Einfallswinkels der Sonnenstrahlen.

2 BE

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Die Wahrscheinlichkeit, dass Max mindestens einen Muffin mit Pudding genommen hat, lässt sich als Gegenereignis von „Max hat nur Muffins mit Heidelbeeren genommen.“ wie folgt berechnen:

$1-\dfrac{32}{40}\cdot \dfrac{31}{39}\cdot \dfrac{30}{38}\approx 0,498$

Die Wahrscheinlichkeit beträgt ca. $50\,\%.$

$A:=$ „Man nimmt zwei Muffins mit der gleichen Füllung.“

$B:=$ „Wenn man drei Muffins nacheinander nimmt, nimmt man mindestens zwei Muffins mit Pudding.“

1. Schritt: Funktionsgleichungen von $\boldsymbol f$ und $\boldsymbol g$ bestimmen

Die lineare Funktion $g$ hat die Steigung $m=1$ und verläuft durch den Punkt $A(0\mid -1,5).$ Die Funktionsgleichung von $g$ lautet also wie folgt:

$g(x)=x-1,5$

Einsetzen der Koordinaten der Punkte $B(4\mid 3)$ und $C(1\mid 6)$ in die Funktionsgleichung von $f$ liefert die folgenden beiden Gleichungen:

$\begin{array}[t]{rll} \text{I} \quad &3&=& 4^2+4\cdot p+q \\[5pt] &3&=& 16+4\cdot p+q \quad \scriptsize \mid\; -16 \\[5pt] &-13&=& 4\cdot p+q \end{array}$

$\begin{array}[t]{rll} \text{II} \quad &6&=& 1^2+p\cdot 1+q \quad \scriptsize \mid\; -1 \\[5pt] &5&=& p+q \end{array}$

Umstellen der Gleichung $\text{II}$ nach $q$ liefert $q=5-p.$ Mit Einsetzen in $\text{I}$ folgt:

$\begin{array}[t]{rll} -13&=& 4\cdot p+(5-p) \\[5pt] -13&=& 3\cdot p+5 \quad \scriptsize \mid\; -5\\[5pt] -18&=& 3\cdot p \quad \scriptsize \mid\; :3\\[5pt] -6&=& p \end{array}$

Damit folgt weiter $q=5-p=5-(-6)=11$

Die Funktionsgleichung von $f$ lautet $f(x)=x^2-6x+11.$

2. Schritt: Graphen auf gemeinsame Punkte untersuchen

$\begin{array}[t]{rll} f(x)&=& g(x) \\[5pt] x^2-6x+11&=& x-1,5 \quad \scriptsize \mid\; -x\\[5pt] x^2-7x+11&=& -1,5 \quad \scriptsize \mid\; +1,5\\[5pt] x^2-7x+12,5&=& 0 \end{array}$

Mit der pq-Formel oder dem Taschenrechner folgt:

$\begin{array}[t]{rll} x_{1,2}&=& -\dfrac{-7}{2}\pm \sqrt{\left(\dfrac{-7}{2}\right)^2-12,5} \\[5pt] &=& \dfrac{7}{2}\pm \sqrt{-0,25}\end{array}$

Da der Wert unter der Wurzel negativ ist, hat die Gleichung keine Lösung und die beiden Graphen somit keinen gemeinsamen Punkt.
Jules Behauptung ist richtig.

Mit dem Satz des Pythagoras lässt sich überprüfen, ob es sich um ein rechtwinkliges Dreieck handelt.

$|\overline{AB}|=\sqrt{(4-0)^2+(3-(-1,5))^2}=\sqrt{36,25}$

$| \overline{AC}|=\sqrt{(1-0)^2+(6-(-1,5))^2}=\sqrt{57,25}$

$| \overline{BC}|=\sqrt{(1-4)^2+(6-3)^2}=\sqrt{18}$

In einem rechtwinkligen Dreieck ist die längste Seite die Hypotenuse. Hier müsste also $\mid \overline{AC}\mid$ die Hypotenuse sein.

$|\overline{AC}|^2= 57,25$

$| \overline{AB}|^2+| \overline{BC}|^2= 36,25+18 =54,25$

Also ist: $|\overline{AC}|^2 \neq | \overline{AB}|^2+| \overline{BC}|^2$

Das Dreieck $ABC$ ist nicht rechtwinklig.

Mit dem Dreisatz gilt:

$:7$

$\cdot 60$ Grau geschwungener Pfeil, der nach rechts unten zeigt.

$\begin{array}{rcl} 7\,\text{m} \,\text{Schatten} & \mathrel{\widehat{=}}& 1,80 \,\text{m}\\[5pt] 1\,\text{m} \,\text{Schatten} & \mathrel{\widehat{\approx}}& 0,257 \,\text{m}\\[5pt] 60\,\text{m} \,\text{Schatten} & \mathrel{\widehat{=}}& 15,4\,\text{m} \end{array}$

$:7$

$\cdot 60$

Der Baum ist ungefähr $15\,\text{m}$ hoch.

Gesucht ist der Winkel $\alpha$ in der Skizze.

Einfallswinkel Sonnenstrahlen - BLF Thüringen 2023

Skizze (nicht maßstabsgerecht)

Dieser lässt sich wie folgt berechnen:

$\begin{array}[t]{rll} \sin(\alpha)&=& \dfrac{1,80\,\text{m}}{7 \,\text{m}} \quad \scriptsize \mid\; \sin^{-1}\\[5pt] \alpha&\approx& 14,9^{\circ} \end{array}$

Der Einfallswinkel hat eine Größe von ungefähr $15^{\circ}.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?