Wahlaufgabe 1

Die Klasse 10b führt ihre Abschlussfeier in einem Garten durch, der die Form eines Vierecks $ABCD$ hat.

Skizze nicht maßstäblich

$\overline{AB\;}\parallel$	$\overline{CD}$
$\overline{AB}=$	$80\,\text{m}$
$\overline{AD}=$	$45\,\text{m}$
$\overline{CD}=$	$65\,\text{m}$
$\alpha=$	$50°$

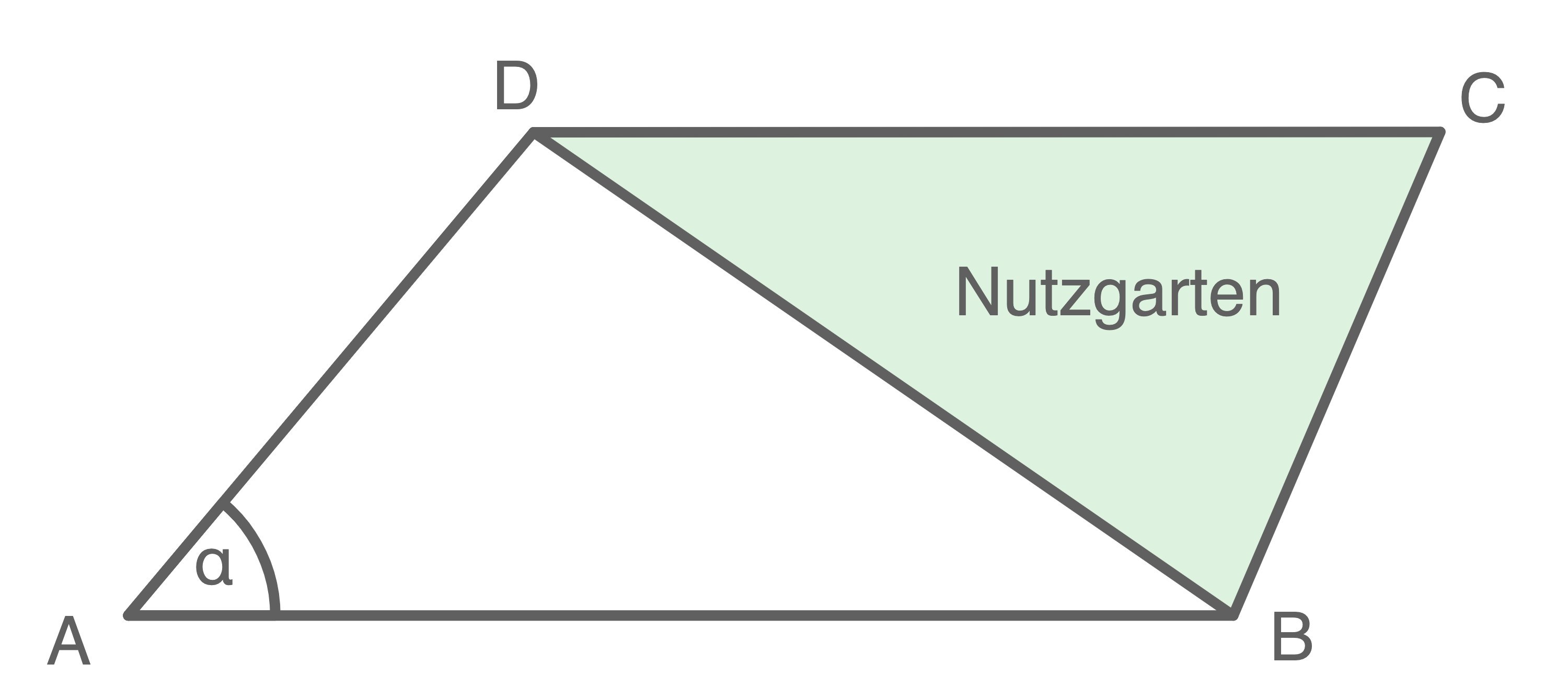
Die Schüler sollen den Nutzgarten nicht betreten. Deshalb wird ein rot-weißes Absperrband von $B$ nach $D$ straff gespannt.

Berechne die Länge des Absperrbandes, wenn zusätzlich $1\,\text{m}$ für die Befestigung eingeplant werden muss.

(2 BE)

Ermittle den prozentualen Anteil der Gartenfläche, die die Klasse 10b zum Feiern nutzen darf.

(4 BE)

Im Garten befindet sich ein Pavillon, der die Form eines Quaders mit aufgesetzter gerader Pyramide hat.

Skizze nicht maßstäblich

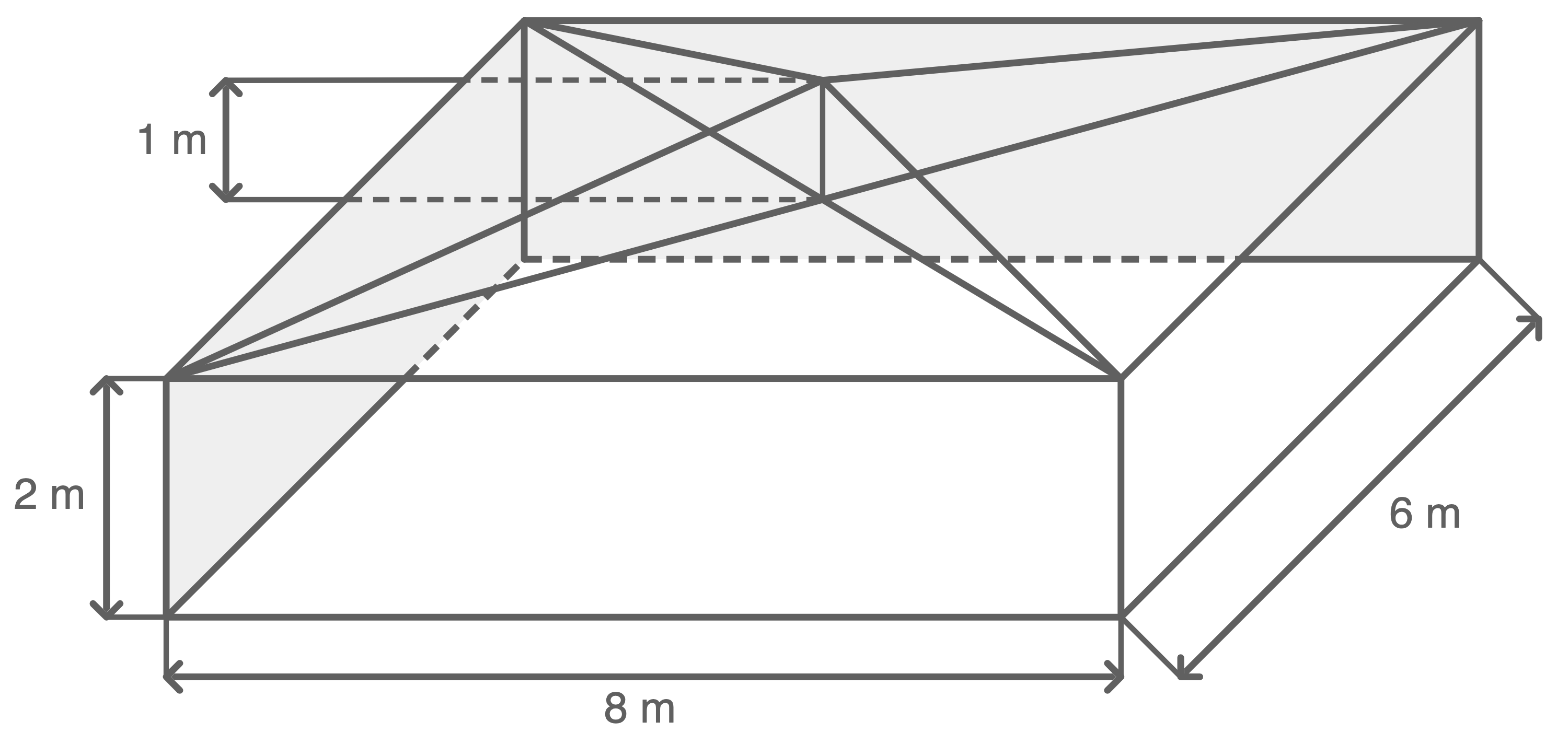Die Dachfläche und zwei benachbarte Seitenflächen des Pavillons sind mit wasserdichter Folie bespannt.
Berechne den Flächeninhalt der benötigten Folie.

(4 BE)

Ein benachbartes Eiscafe bietet ein kleines Gewinnspiel an. Ein Gefäß enthält drei Kugeln, die mit den Buchstaben E, I und S beschriftet sind. Jeder Schüler darf dreimal ohne Zurücklegen ziehen. Die Kugeln werden in der Reihenfolge, in der sie gezogen werden, abgelegt. Ergibt sich das Wort „EIS“, hat man eine Eisportion gewonnen. In der Klasse 10b sind 24 Schülerinnen und Schüler.
Ermittle die zu erwartende Anzahl an gewonnenen Eisportionen.

(2 BE)

An einem Eisautomaten können jeweils zwei Kugeln Eis entnommen werden. Der Automat gibt die Eissorten zufällig aus. Die Wahrscheinlichkeit dafür, dass bei zwei Kugeln mindestens eine Kugel Erdbeereis dabei ist, beträgt 0,51.
Bestimme die Wahrscheinlichkeit dafür, dass der Kunde genau zwei Kugeln Erdbeereis erhält.

(3 BE)

Die Länge der Strecke $\overline{BD}$ kann mit dem Kosinussatz im Dreieck $ABD$ berechnet werden.

Rechenweg anzeigen

Der Taschenrechner liefert $\overline{BD}\approx 62\,\text{m}.$ Da für die Befestigung zusätzlich ein Meter Länge eingeplant werden muss, ist das Absperrband ungefähr 63 m lang.

Um den prozentualen Anteil der Gartenfläche zu bestimmen, muss der Flächeninhalt $A_1$ sowie der gesamte Flächeninhalt des Gartens bestimmt werden.

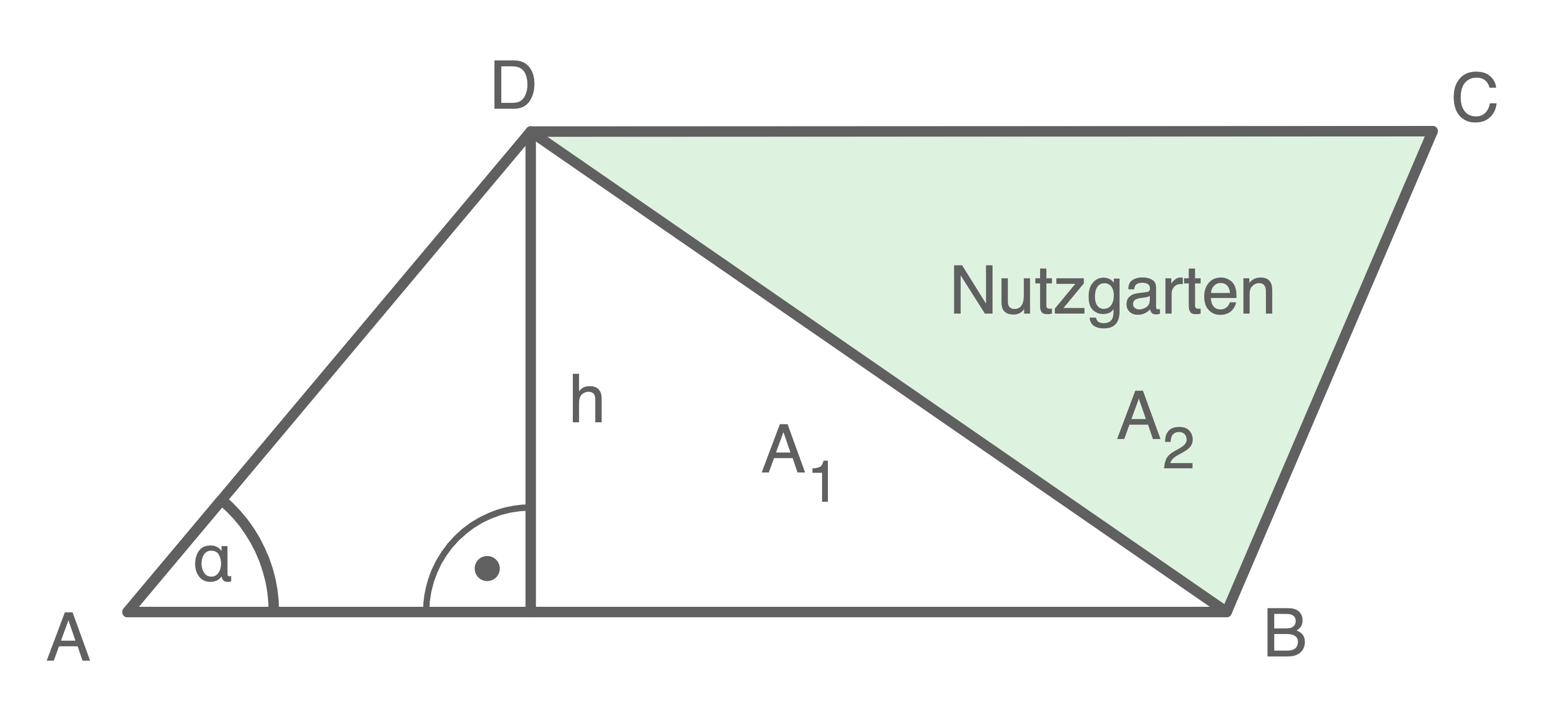Dazu wird zunächst die Höhe $h$ der Dreiecke berechnet:

$\begin{array}[t]{rll} \sin(\alpha)&=& \dfrac{h}{\overline{AD}} \quad \scriptsize \mid\; \cdot \overline{AD} \\[5pt] \sin(\alpha)\cdot \overline{AD}&=& h \\[5pt] \sin(50°)\cdot 45\,\text{m}&=& h \\[5pt] 34,5\,\text{m}&\approx& h \end{array}$

Für den Flächeninhalt des Dreiecks $ABD$ folgt:

$\begin{array}[t]{rll} A_1&=& \dfrac{1}{2}\cdot \overline{AB}\cdot h \\[5pt] &\approx& \dfrac{1}{2}\cdot 80\,\text{m}\cdot 34,5\,\text{m} \\[5pt] &\approx& 1\,379\,\text{m}^2 \end{array}$

Für den Flächeninhalt des Dreiecks $BCD$ gilt:

$\begin{array}[t]{rll} A_2&=& \dfrac{1}{2}\cdot \overline{CD}\cdot h \\[5pt] &\approx& \dfrac{1}{2}\cdot 65\,\text{m}\cdot 34,5\,\text{m} \\[5pt] &\approx& 1\,120\,\text{m}^2 \end{array}$

Damit gilt für den Flächeninhalt der Gesamten Gartenfläche:

$\begin{array}[t]{rll} A&=& A_1+A_2 \\[5pt] &\approx& 1\,379\,\text{m}^2+ 1\,120\,\text{m}^2\\[5pt] &\approx& 2\,500\,\text{m}^2 \end{array}$

Der prozentuale Anteil der Fläche $A_1$ lässt sich nun wie folgt berechnen:

$\begin{array}[t]{rll} \dfrac{p}{A_1}&=& \dfrac{100\,\%}{A} \quad \scriptsize \mid\;\cdot A_1 \\[5pt] p&=& \dfrac{100\,\%}{A}\cdot A_1 \\[5pt] p&\approx& \dfrac{100\,\%}{2\,500\,\text{m}}\cdot 1\,379\,\text{m}^2 \\[5pt] p&\approx& 55\,\% \end{array}$

Der prozentuale Anteil der Gartenfläche, den die 10b für ihre Feier nutzen kann, beträgt ungefähr 55 %.

Der Gesamtflächeninhalt der Folie setzt sich aus dem Flächeninhalt der beiden rechteckigen Seitenflächen und dem Flächeninhalt der Oberfläche der Pyramide zusammen.

Flächeninhalt der Seitenteile berechnen:

$\begin{array}[t]{rll} A_{S1}&=& 6\,\text{m}\cdot 2\,\text{m}\\[5pt] &=& 12\,\text{m}^2\\[5pt] A_{S2}&=& 8\,\text{m}\cdot 2\,\text{m}\\[5pt] &=& 16\,\text{m}^2 \\[5pt] \end{array}$

Außerdem wird der Flächeninhalt der dreieckigen Seitenflächen der Pyramide benötigt.

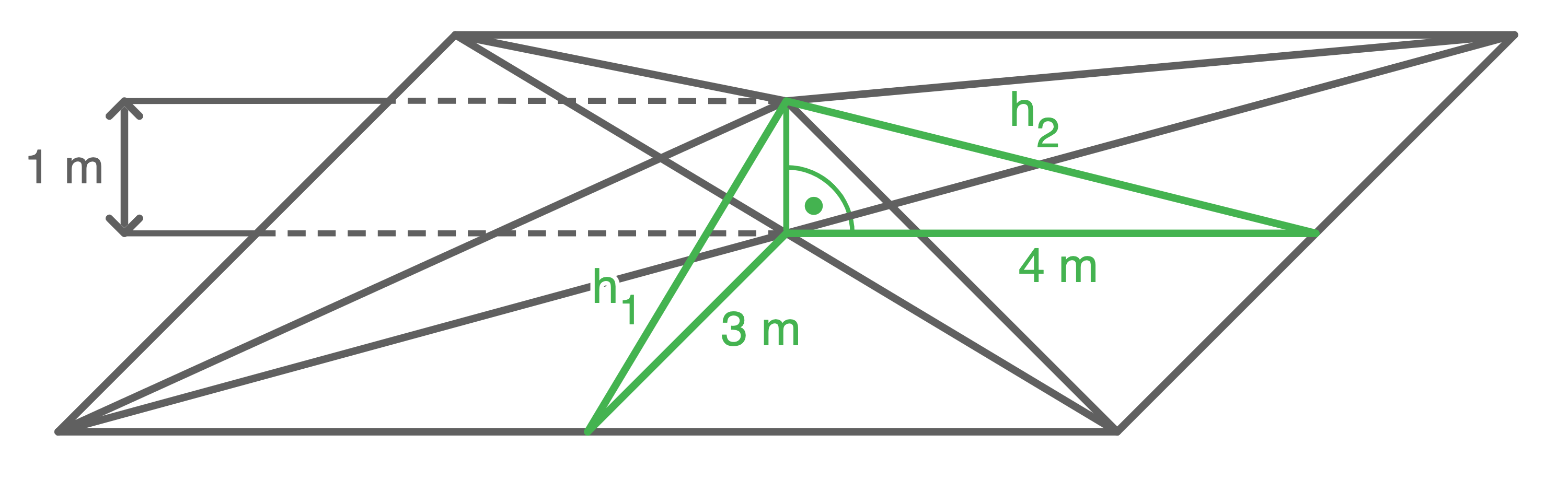Die Höhen der Dreiecke können mit dem Satz des Pythagoras berechnet werden:

$\begin{array}[t]{rll} h_1^2&=& (3\,\text{m})^2+(1\,\text{m})^2 \\[5pt] h_1^2&=& 10\,\text{m}^2 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt] h_1&=& \sqrt{10}\,\text{m} \end{array}$

$\begin{array}[t]{rll} h_2^2&=& (4\,\text{m})^2+(1\,\text{m})^2 \\[5pt] h_2^2&=& 17\,\text{m}^2 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt] h_2&=& \sqrt{17}\,\text{m} \end{array}$

Damit können nun die Flächeninhalte der Dreiecke berechnet werden:

$\begin{array}[t]{rll} A_{D1}&=& \dfrac{1}{2}\cdot 8\,\text{m} \cdot h_1 \\[5pt] &\approx& \dfrac{1}{2}\cdot 8\,\text{m} \cdot \sqrt{10}\,\text{m} \\[5pt] &=& 4\sqrt{10}\,\text{m}^2\\[5pt] A_{D2}&=& \dfrac{1}{2}\cdot 6\,\text{m} \cdot h_2\\[5pt] &\approx& \dfrac{1}{2}\cdot 6\,\text{m} \cdot \sqrt{17}\,\text{m}\\[5pt] &=& 3\sqrt{17}\,\text{m} \end{array}$

Der gesamte Flächeninhalt der benötigten Folie lässt sich schließlich wie folgt berechnen:

$\begin{array}[t]{rll} A&=& A_{S1}+A_{S2}+2\cdot A_{D1}+2\cdot A_{D2} \\[5pt] &\approx& 12\,\text{m}^2+16\,\text{m}^2+2\cdot 4\sqrt{10}\,\text{m}^2 + 2 \cdot 3\sqrt{17}\,\text{m}\\[5pt] &\approx& 78\,\text{m}^2 \end{array}$

Der Flächeninhalt der Folie beträgt etwa $78\,\text{m}^2.$

Zunächst muss die Wahrscheinlichkeit für das Erzielen der Reihenfolge „EIS“ berechnet werden. Da es sich um Ziehen ohne Zurücklegen handelt, gilt:

$p=\dfrac{1}{3}\cdot \dfrac{1}{2}\cdot \dfrac{1}{1}=\dfrac{1}{6}$

Die zu erwartende Anzahl an gewonnenen Eisportionen lässt sich mit dem Erwartungswert berechnen. Für $n=24$ Schülerinnen und Schüler folgt:

$E=n\cdot p=24\cdot \dfrac{1}{6}=4$

Die zu erwartende Anzahl an gewonnenen Eiskugeln beträgt 4.

$E:$ Kugel Erdbeereis

Zunächst wird die Wahrscheinlichkeit $p$ berechnet, dass der Kunde bei der zufälligen Entnahme ein Erdbeereis erhält. Bekannt ist:

$P(\text{„mindestens eine Kugel Erdbeereis“})$

$\begin{array}[t]{rll} &=& P(E\overline{E})+P(\overline{E}E)+P(EE) \\[5pt] &=& 1-P(\overline{EE}) \\[5pt] &=& 0,51 \end{array}$

Daraus folgt:

$\begin{array}[t]{rll} P(\overline{EE})&=& 0,49 \\[5pt] (1-p)^2&=& 0,49 \end{array}$

Der Taschenrechner liefert $p=0,3.$ Die Lösung $p=1,7$ kommt im Sachzusammenhang nicht infrage. Es folgt:

$P(\text{„genau zwei Kugeln Eis“})$

$\begin{array}[t]{rll} &=& P(EE) \\[5pt] &=& p^2 \\[5pt] &=& 0,3^2 \\[5pt] &=& 0,09 \end{array}$

Die Wahrscheinlichkeit dafür, dass der Kunde genau zwei Kugeln Erdbeereis erhält, beträgt 9 %.