Pflichtaufgabe 2 – Mit Hilfsmitteln
1.
In einer Socke befinden sich fünf beschriftete Golfbälle.
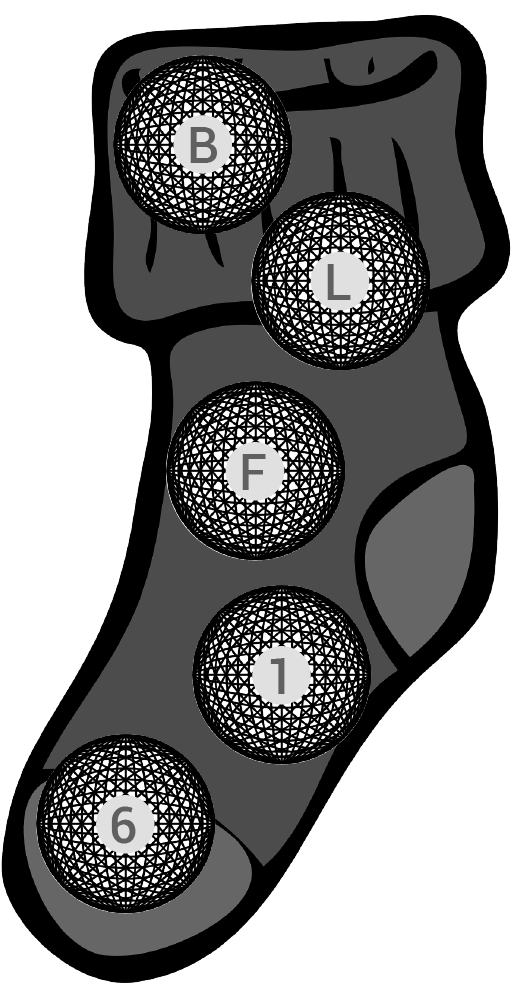 Berechne die Wahrscheinlichkeiten folgender Ereignisse:
Berechne die Wahrscheinlichkeiten folgender Ereignisse:

A:=
„Beim Ziehen ohne Zurücklegen ist der zweite Buchstabe ein  .“
.“
B:=
„Beim Ziehen ohne Zurücklegen wird die Zeichenfolge 



 gezogen.“
gezogen.“
C:=
„Beim Ziehen mit Zurücklegen wird nicht die Zeichenfolge 



 gezogen.“
gezogen.“
(4 BE)
2.
In einem rechtwinkligen Koordinatensystem sind die Punkte 
 und
und  gegeben.
gegeben.
a)
Zeige rechnerisch, dass das Dreieck  rechtwinklig ist.
rechtwinklig ist.
(3 BE)
b)
Berechne den Flächeninhalt des Dreiecks  .
.
(1 BE)
c)
Aus den Punkten 

 und
und  soll ein Viereck gebildet werden, dessen Flächeninhalt doppelt so groß ist wie der des Dreiecks
soll ein Viereck gebildet werden, dessen Flächeninhalt doppelt so groß ist wie der des Dreiecks 
Gib die Koordinaten eines solchen Punktes an.
an.
Gib die Koordinaten eines solchen Punktes
(1 BE)
d)
Begründe, dass es keine Funktion  mit
mit 
 geben kann, deren Graph durch die Punkte
geben kann, deren Graph durch die Punkte  ,
,  und
und  verläuft.
verläuft.
(2 BE)
3.
Zur Landesrunde der Mathematikolympiade gab es 2014 für jeden Teilnehmer eine Pyramide mit quadratischer Grundfläche.
Alle Kanten sind 10 cm lang.
Berechne das Volumen und den Oberflächeninhalt dieser Pyramide.
Alle Kanten sind 10 cm lang.
Berechne das Volumen und den Oberflächeninhalt dieser Pyramide.

(4 BE)
1.
Wenn der zweite Buchstabe ein  ist, muss die erste Kugel mit einer der restlichen vier Möglichkeiten beschriftet sein:
ist, muss die erste Kugel mit einer der restlichen vier Möglichkeiten beschriftet sein:
 Bei jedem Zug gibt es nur eine Möglichkeit, die benötigte Kugel zu ziehen. Bei jedem Zug nimmt dabei die Anzahl der Kugeln um eins ab:
Bei jedem Zug gibt es nur eine Möglichkeit, die benötigte Kugel zu ziehen. Bei jedem Zug nimmt dabei die Anzahl der Kugeln um eins ab:
 Um die Wahrscheinlichkeit von Ereignis
Um die Wahrscheinlichkeit von Ereignis  zu berechnen, kann das Gegenereignis verwendet werden:
zu berechnen, kann das Gegenereignis verwendet werden:
2.
a)
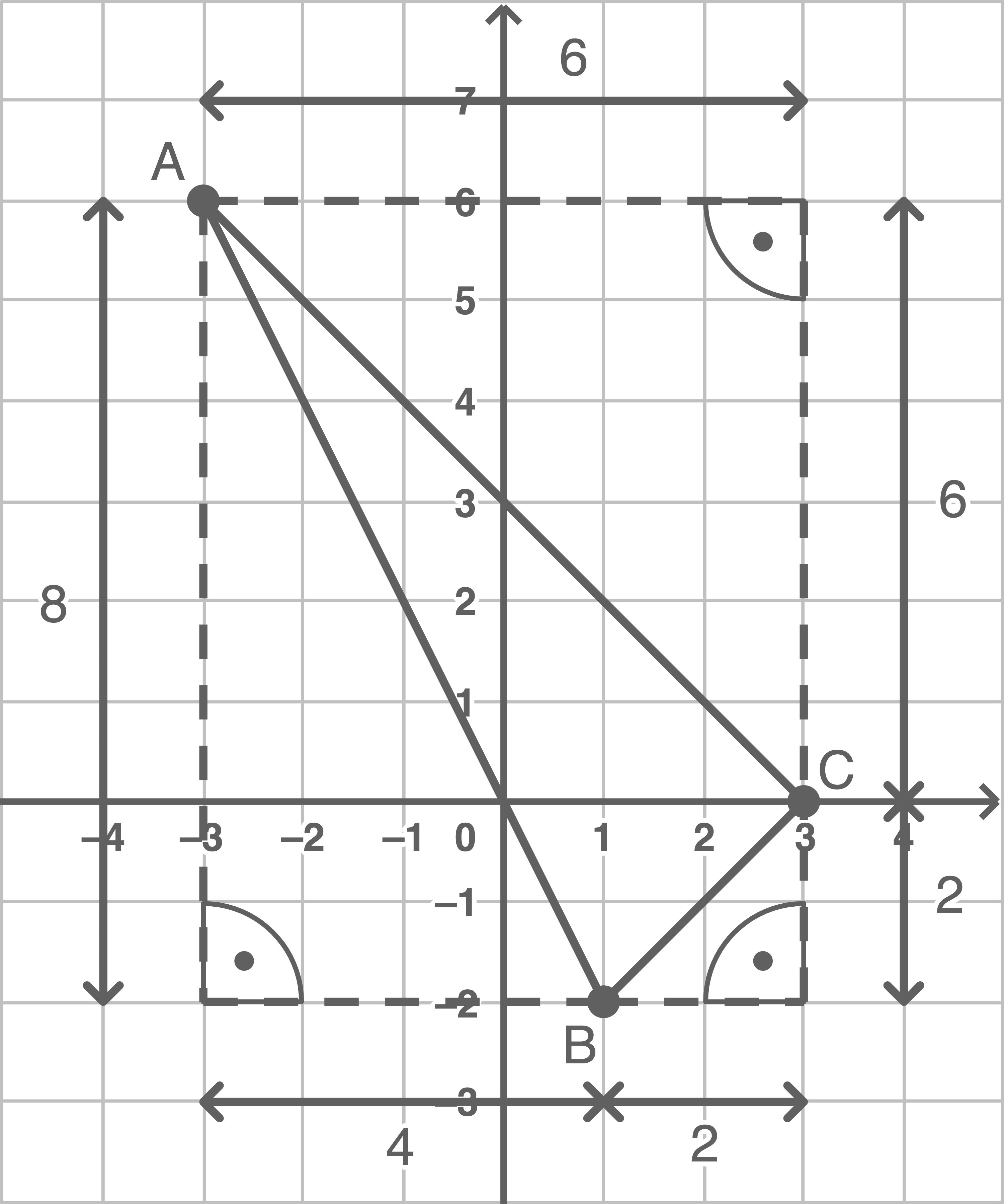
Wenn das Dreieck rechtwinklig ist, muss nach dem Satz des Pythagoras gelten:
 Die Seitenlängen des Dreiecks können wiederum mit dem Satz des Pythagoras berechnet werden:
Die Seitenlängen des Dreiecks können wiederum mit dem Satz des Pythagoras berechnet werden:
![\(\begin{array}[t]{rll}
\overline{AB}^2&=& 8^2+4^2 \\[5pt]
&=& 64+16 \\[5pt]
&=& 80
\end{array}\)](https://www.schullv.de/resources/formulas/f5dcc76bb138626f6bda6fca596e23353f36975ccb22cb0563e822566d3f55d3_light.svg)
![\(\begin{array}[t]{rll}
\overline{AC}^2&=& 6^2+6^2 \\[5pt]
&=& 36+36 \\[5pt]
&=& 72
\end{array}\)](https://www.schullv.de/resources/formulas/57273fe3605db3cc0d497520f4ed8a494355ea87abed98ca9dfd422408796b05_light.svg)
![\(\begin{array}[t]{rll}
\overline{BC}^2&=& 2^2+2^2 \\[5pt]
&=& 4+4 \\[5pt]
&=& 8
\end{array}\)](https://www.schullv.de/resources/formulas/75b5858047887d5619c728c98c844b8d5f50a12fe7a493c2124884a9f64eca43_light.svg)
Es gilt:

b)
Mit Teilaufgabe a) gilt  und
und  Mit der Formel für den Flächeninhalt eines Dreiecks folgt:
Mit der Formel für den Flächeninhalt eines Dreiecks folgt:
![\(\begin{array}[t]{rll}
A_D&=& \dfrac{1}{2}\cdot \overline{AC}\cdot \overline{BC} \\[5pt]
&=& \dfrac{1}{2}\cdot \sqrt{72}\cdot \sqrt{8}\\[5pt]
&=& 12\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/11e7bf40907f5fd40a864254bda3ce1f4463ae7e12d70c861261b5633f3f0868_light.svg) Der Flächeninhalt des Dreiecks beträgt 12 Flächeneinheiten.
Der Flächeninhalt des Dreiecks beträgt 12 Flächeneinheiten.
c)
Am einfachsten ist es, das Dreieck zu einem Rechteck zu ergänzen. Ein möglicher Punkt dafür ist der Punkt 
d)
Eine Funktion der Form  hat keine Nullstelle. Der Punkt
hat keine Nullstelle. Der Punkt  liegt jedoch auf der
liegt jedoch auf der  -Achse und würde deshalb einer Nullstelle einer möglichen Funktion entsprechen. Daher kann es keine Funktion dieser Form geben, die durch alle Punkte
-Achse und würde deshalb einer Nullstelle einer möglichen Funktion entsprechen. Daher kann es keine Funktion dieser Form geben, die durch alle Punkte 
 und
und  geht.
geht.
3.
Oberflächeninhalt berechnen
Der Oberflächeninhalt einer Pyramide setzt sich zusammen aus dem Flächeninhalt der Grundfläche und dem Flächeninhalt der Seitenflächen. Der Flächeninhalt der quadratischen Grundfläche lässt sich wie folgt berechnen:
![\(\begin{array}[t]{rll}
A_G&=& a\cdot a \\[5pt]
&=& 10\,\text{cm}\cdot 10\,\text{cm} \\[5pt]
&=& 100\,\text{cm}^2
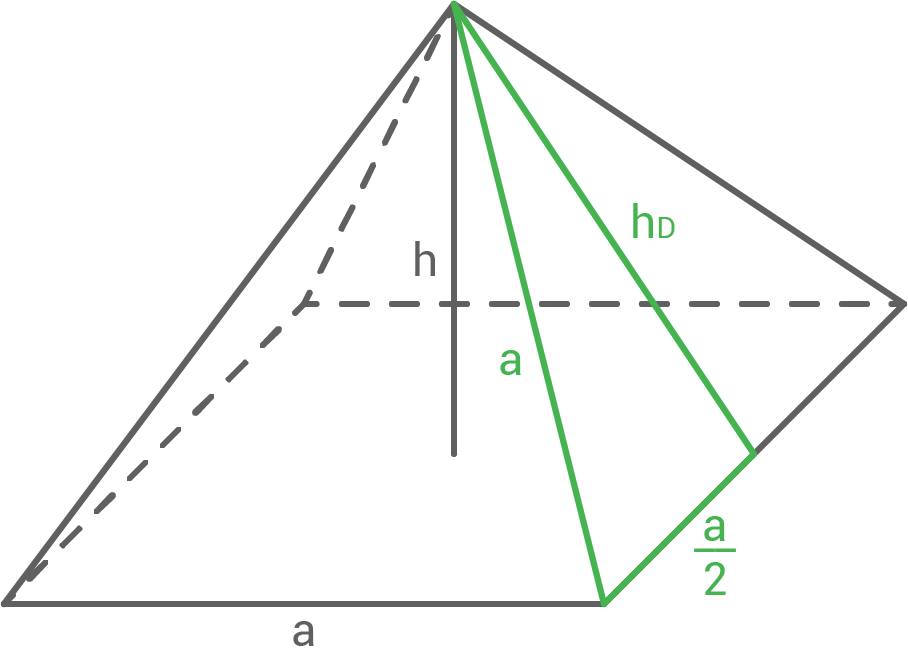
\end{array}\)](https://www.schullv.de/resources/formulas/9b9465c94030f177d8e381f597d6c7d9a3dc886ef9cade78f575a25e2eafde7e_light.svg) Um den Flächeninhalt der dreieckigen Seitenflächen zu berechnen, muss zunächst die Höhe
Um den Flächeninhalt der dreieckigen Seitenflächen zu berechnen, muss zunächst die Höhe  eines solchen Dreiecks berechnet werden. Dazu wird der Satz des Pythagoras verwendet:
eines solchen Dreiecks berechnet werden. Dazu wird der Satz des Pythagoras verwendet:
![\(\begin{array}[t]{rll}
a^2&=& \left(\dfrac{a}{2}\right)^2+h_D^2 \\[5pt]
(10\,\text{cm})^2&=&(5\,\text{cm})^2+h_D^2 \\[5pt]
100\,\text{cm}^2&=& 25\,\text{cm}^2+h_D^2 \quad \scriptsize \mid\;-25\,\text{cm}^2 \\[5pt]
75\,\text{cm}^2&=& h_D^2 \quad \scriptsize \mid\;\sqrt{\;} \\[5pt]
8,7\,\text{cm}&\approx& h_D\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/a7af23f0069ddeb6f8d0dd18be09a6da9357e67a1fc24437fbc353c35b49d485_light.svg) Damit kann der Flächeninhalt eines Dreiecks berechnet werden:
Damit kann der Flächeninhalt eines Dreiecks berechnet werden:
![\(\begin{array}[t]{rll}
A_D&=&\dfrac{1}{2}\cdot a \cdot h_D \\[5pt]
&\approx&\dfrac{1}{2}\cdot 10\,\text{cm}\cdot 8,7\,\text{cm} \\[5pt]
&\approx& 43,5\,\text{cm}^2 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/9c82a2c211e5d10efde0ca28793457092efcb0945d91eb298df1a04fa4fb8c5c_light.svg) Nun kann der Oberflächeninhalt der Pyramide berechnet werden:
Nun kann der Oberflächeninhalt der Pyramide berechnet werden:
![\(\begin{array}[t]{rll}
A_O&=&A_G+4\cdot A_D \\[5pt]
&\approx&100\,\text{cm}^2+4\cdot 43,5\,\text{cm}^2\\[5pt]
&=& 274\,\text{cm}^2\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/fdb57b7233e172e8a3baa61cab094fc0543c1846e130b3799546ab1434980d95_light.svg) Der Oberflächeninhalt der Pyramide beträgt
Der Oberflächeninhalt der Pyramide beträgt  Volumen berechnen
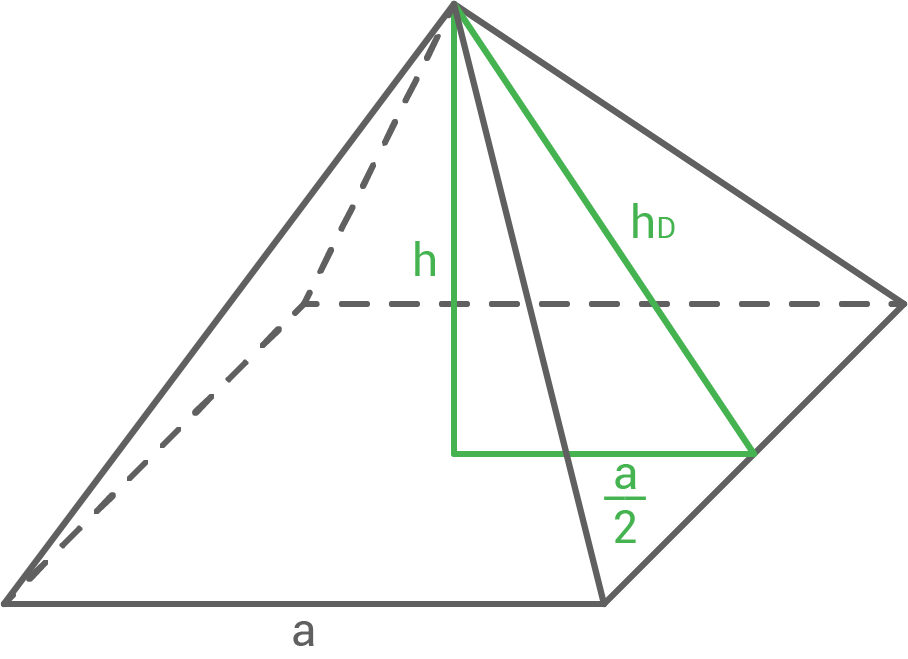
Um das Volumen der Pyramide berechnen zu können, wird die Höhe
Volumen berechnen
Um das Volumen der Pyramide berechnen zu können, wird die Höhe  benötigt. Diese lässt sich wieder mit dem Satz des Pythagoras berechnen:
benötigt. Diese lässt sich wieder mit dem Satz des Pythagoras berechnen:
![\(\begin{array}[t]{rll}
h_D^2&=& \left(\dfrac{a}{2}\right)^2+h^2 \\[5pt]
(8,7\,\text{cm})^2&=&(5\,\text{cm})^2+h^2 \\[5pt]
75\,\text{cm}^2&=& 25\,\text{cm}^2+h^2 \quad \scriptsize \mid\;-25\,\text{cm}^2 \\[5pt]
50\,\text{cm}^2&=& h^2 \quad \scriptsize \mid \sqrt{\;} \\[5pt]
7,1\,\text{cm}&=& h \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/39dbff92b3ec15c2bfef0431a2197c58dc1c513cfbff744c96d4c39f13902d4e_light.svg) Damit lässt sich das Volumen der Pyramide wie folgt berechnen:
Damit lässt sich das Volumen der Pyramide wie folgt berechnen:
![\(\begin{array}[t]{rll}
V_P&=&\dfrac{1}{3}\cdot A_G\cdot h \\[5pt]
&=&\dfrac{1}{3}\cdot 100\,\text{cm}^2\cdot 7,1\,\text{cm} \\[5pt]
&=& 236,7\,\text{cm}^3 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/b007ab0e96f174fd4a4c8f1fb85985725f0caa7ab786e5c450a4047c564ab537_light.svg) Das Volumen der Pyramide beträgt
Das Volumen der Pyramide beträgt 

