Wahlaufgabe 1

Folgende Werte von zwei Sachverhalten sind gegeben:

Höhe über N.N. in km	Luftdruck in hPa
$0$	$1\,013$
$1$	$896$
$2$	$792$
$3$	$700$
$4$	$619$

Zeit in h	Füllhöhe eines Wasserbeckens in cm
$0$	$130$
$1$	$104$
$2$	$78$
$3$	$52$
$4$	$26$

Entscheide für jeden dieser beiden Sachverhalte, ob ein linearer oder exponentieller Zusammenhang besteht. Begründe deine Entscheidung.

(2 BE)

Berechne den Luftdruck, der in etwa 8 000 m Höhe erreicht wird.

(2 BE)

Ermittle, nach wie vielen Minuten die Füllhöhe im Wasserbecken 40 cm beträgt.

(2 BE)

Der Barockgarten eines Schlosses wurde vermessen.
Die Ergebnisse sind in der Skizze dargestellt.

Berechne den Flächeninhalt des Barockgartens in Quadratmeter.

(5 BE)

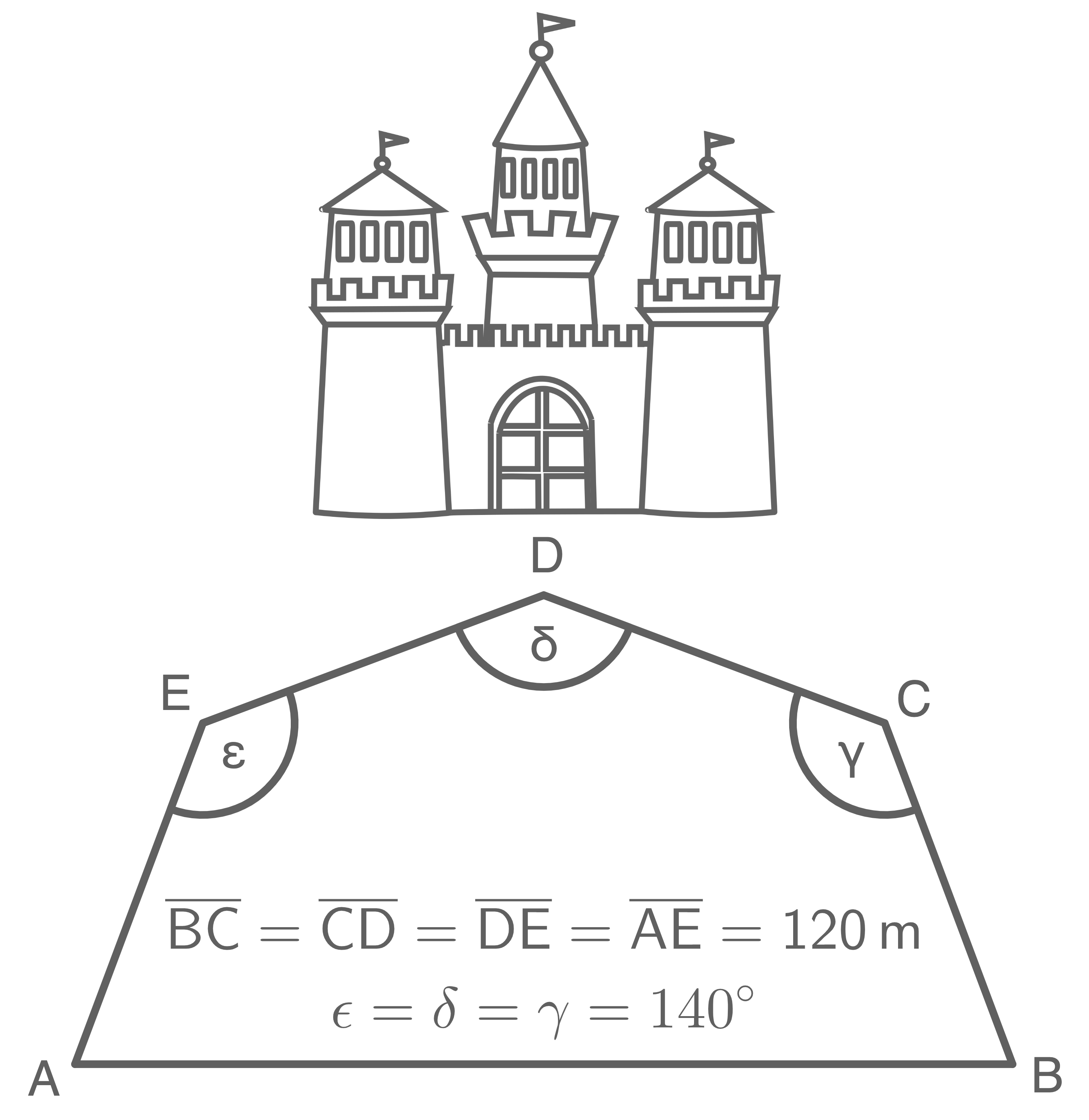
Skizze nicht maßstäblich

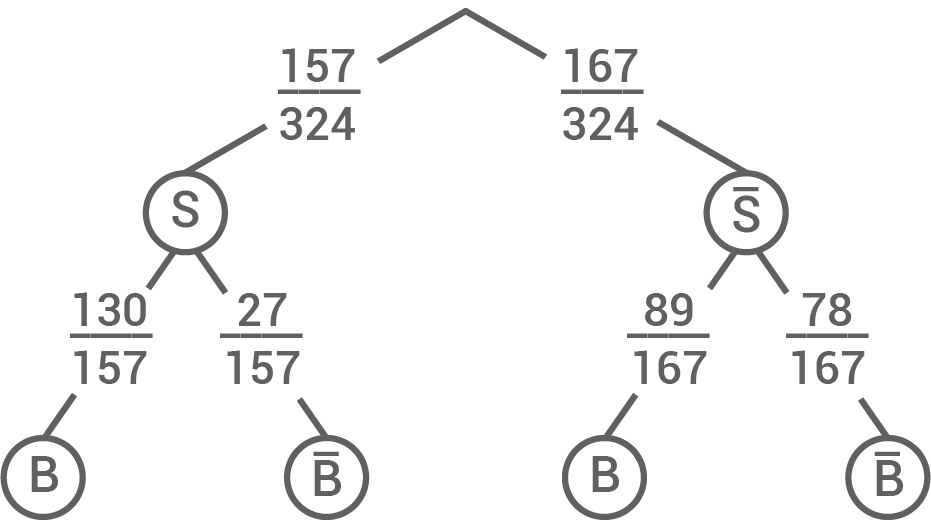
Max hat bei Facebook 324 Freunde. Von diesen Freunden haben 105 ihren Beziehungsstatus nicht angegeben. Max weiß sicher, dass genau 167 seiner Freunde nicht Single sind. Außerdem haben 130 Singles ihren Beziehungsstatus angegeben.

Bestimme die Wahrscheinlichkeit, dass ein zufällig ausgewählter Facebook-Freund von Max Single ist und diesen Status nicht angegeben hat.

Nutze dafür eine vollständig ausgefüllte Vierfeldtafel oder ein vollständig beschriftetes Baumdiagramm.

(4 BE)

Für die erste Tabelle gilt der Zusammenhang:

$\dfrac{p(h+1)}{p(h)}\approx 0,88$

In jedem Intervall gibt es näherungsweise die gleiche prozentuale Abnahme, deshalb handelt es sich um eine exponentielle Abnahme.

Für die zweite Tabelle gilt der Zusammenhang:

$h(t+1)-h(t)=-26$

In jedem Intervall gibt es die gleiche absolute Abnahme, deshalb handelt es sich um einen linearen Zusammenhang.

Zunächst muss die Funktionsgleichung für den Luftdruck in Abhängigkeit von der Höhe bestimmt werden. Nach Teilaufgabe a) handelt es sich um ein exponentielles Wachstum mit der allgemeinen Funktionsgleichung $f(x)=a\cdot b^x.$ Als Wert $b$ wird der Quotient $b=0,88$ gewählt und der Startwert $a$ ist durch den Luftdruck auf Meeresspiegelhöhe mit $a=1\,013$ gegeben.

Der Luftdruck lässt sich folglich mit der Gleichung $p(h)=1\,013\cdot 0,88^h$ berechnen. Dabei steht $h$ für die Höhe über dem Meeresspiegel in $\text{km}.$

Gesucht ist nun der Luftdruck in 8 Kilometern Höhe:

$p(8)=1\,013\cdot0,88^{8}\approx 364,3$

Der Druck in $8\,000\;\text{m}$ Höhe beträgt ca. $364,3\;\text{hPa}.$

In Teilaufgabe a) wurde ein linearer Zusammenhang mit einer Differenz von -26 feststellen. Der Startwert beträgt 130 cm. Die Füllhöhe des Wassers in cm in Abhängigkeit von der Zeit t in Stunden lässt sich daher mit folgender Formel berechnen:

$h(t)=-26\cdot t+130$

Gesucht ist die Lösung der Gleichung $h(t)=40:$

$\begin{array}[t]{rll} h(t)&=& 40 \\[5pt] -26\cdot t+130&=& 40 \quad \scriptsize \mid\; -130\\[5pt] -26t &=& -90 \quad \scriptsize \mid\;: (-26) \\[5pt] t&\approx& 3,46\quad \scriptsize \\[5pt] \end{array}$

Nach ca. 3,46 Stunden ist die Füllhöhe von 40 Metern erreicht. Durch Multiplikation mit 60 ergibt sich damit eine Zeit von 208 Minuten.

Die Figur setzt sich aus einem Rechteck und drei Dreiecken zusammen.

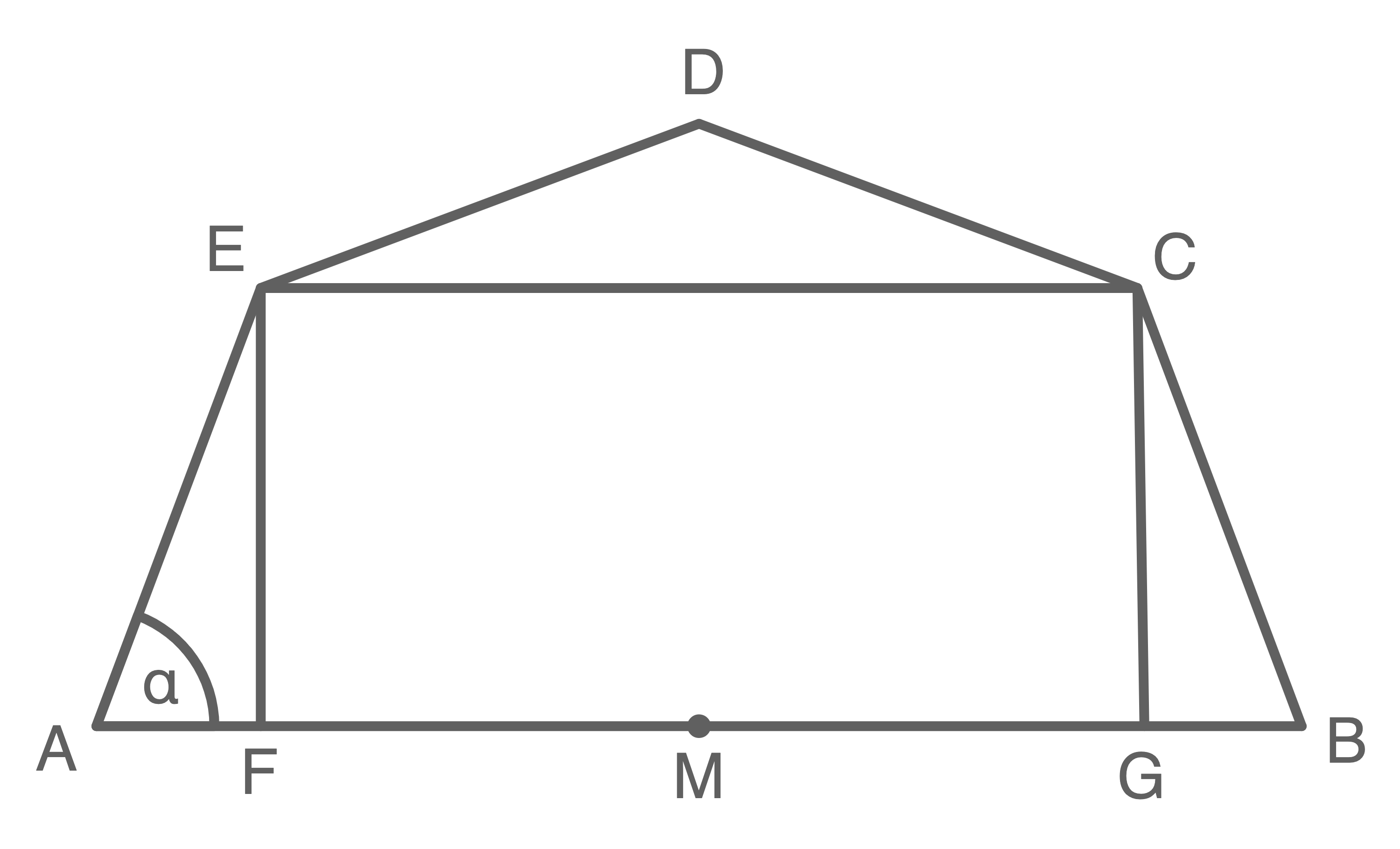Flächeninhalt des Dreiecks CDE berechnen:

$\begin{array}[t]{rll} A_{CDE}&=& \dfrac{1}{2}\cdot \overline{CD}\cdot \overline{DE}\cdot \sin (\delta) \\[5pt] &=& \dfrac{1}{2}\cdot 120\,\text{m} \cdot 120\,\text{m}\cdot \sin (140^°) \\[5pt] &=& 4\,628\,\text{m}^2 \end{array}$

Flächeninhalt des Dreiecks AEF berechnen:

Mit der Innenwinkelsumme des Vierecks $AMDE$ folgt:

$\begin{array}[t]{rll} \alpha&=& 360°-90°-\varepsilon-\dfrac{\delta}{2} \\[5pt] &=& 360°-90°-140°-\dfrac{140°}{2} \\[5pt] &=& 60° \end{array}$

Damit können im Dreieck $AEF$ die Längen der Katheten berechnet werden:

$\begin{array}[t]{rll} \sin (\alpha) &=& \dfrac{\overline{EF}}{\overline{AE}} \quad \scriptsize \mid\;\cdot \overline{AE} \\[5pt] \sin (\alpha)\cdot \overline{AE} &=& \overline{EF} \\[5pt] \sin (60°)\cdot 120\,\text{m} &=& \overline{EF} \\[5pt] 103,9\,\text{m}&\approx& \overline{EF} \end{array}$

$\begin{array}[t]{rll} \cos (\alpha) &=& \dfrac{\overline{AF}}{\overline{AE}} \quad \scriptsize \mid\;\cdot \overline{AE} \\[5pt] \cos (\alpha)\cdot \overline{AE} &=& \overline{AF} \\[5pt] \cos (60°)\cdot 120\,\text{m} &=& \overline{AF} \\[5pt] 60\,\text{m}&=& \overline{AF} \end{array}$

Der Flächeninhalt des Dreiecks $AEF$ ergibt sich damit zu:

$\begin{array}[t]{rll} A_{AEF}&=& \dfrac{1}{2}\cdot \overline{AF}\cdot \overline{EF} \\[5pt] &=& \dfrac{1}{2}\cdot 60\,\text{m}\cdot 103,9\,\text{m} \\[5pt] &=& 3\,117\,\text{m}^2 \end{array}$

Aufgrund der Symmetrie gilt außerdem $A_{AEF}=A_{BCG}=3\,117\,\text{m}^2.$

Flächeninhalt des Rechtecks CEFG berechnen

Die Länge der Seite $\overline{CE}$ lässt sich mit dem Kosinussatz berechnen:

Rechenweg anzeigen

$\overline{CE}= 225,5\,\text{m}$

Mit der bereits berechneten Länge $\overline{EF}\approx 103,9\,\text{m}$ folgt für den Flächeninhalt des Rechtecks $CEFG:$

$\begin{array}[t]{rll} A_{CEFG}&=& \overline{EF}\cdot \overline{CE} \\[5pt] &=& 103,9\,\text{m}\cdot 225,5\,\text{m} \\[5pt] &\approx& 23\,429 \,\text{m}^2 \end{array}$

Gesamten Flächeninhalt der Figur berechnen

$\begin{array}[t]{rll} A&=& A_{CDE}+2\cdot A_{AEF}+A_{CEFG} \\[5pt] &\approx& 4\,628\,\text{m}^2+2\cdot 3\,117\,\text{m}^2+23\,429 \,\text{m}^2\\[5pt] &=& 34\,291\,\text{m}^2 \end{array}$

Der gesamte Flächeninhalt beträgt ca. $34\,291\,\text{m}^2$ .

$S:$ Single
$B:$ Beziehungsstatus angegeben

Lösung mit Vierfeldertafel

	$B$	$\overline{B}$
$S$	$\boldsymbol{130}$	$27$	$157$
$\overline{S}$	$89$	$78$	$\boldsymbol{167}$
	$219$	$\boldsymbol{105}$	$\boldsymbol{324}$

Gesucht ist die Wahrscheinlichkeit des Ereignisses $S\cap \overline{B}.$ Diese ist gegeben durch den Anteil der Freunde, auf die dieses Ereignis zutrifft, an allen Facebook-Freunden. Die zur Berechnung benötigten Werte können der Vierfeldertafel entnommen werden:

$P(S\cap \overline{B})=\dfrac{27}{324}=\dfrac{1}{12}\approx 0,083$

Die gesuchte Wahrscheinlichkeit beträgt ungefähr 8,3 %.

Lösung mit Baumdiagramm

Nach der 1. Pfadregel gilt:

$P(S \cap \overline{B})=\dfrac{157}{324} \cdot \dfrac{27}{157}=\dfrac{1}{12} \approx 0,083$

Die gesuchte Wahrscheinlichkeit beträgt ungefähr 8,3 %.