Wahlaufgabe 2

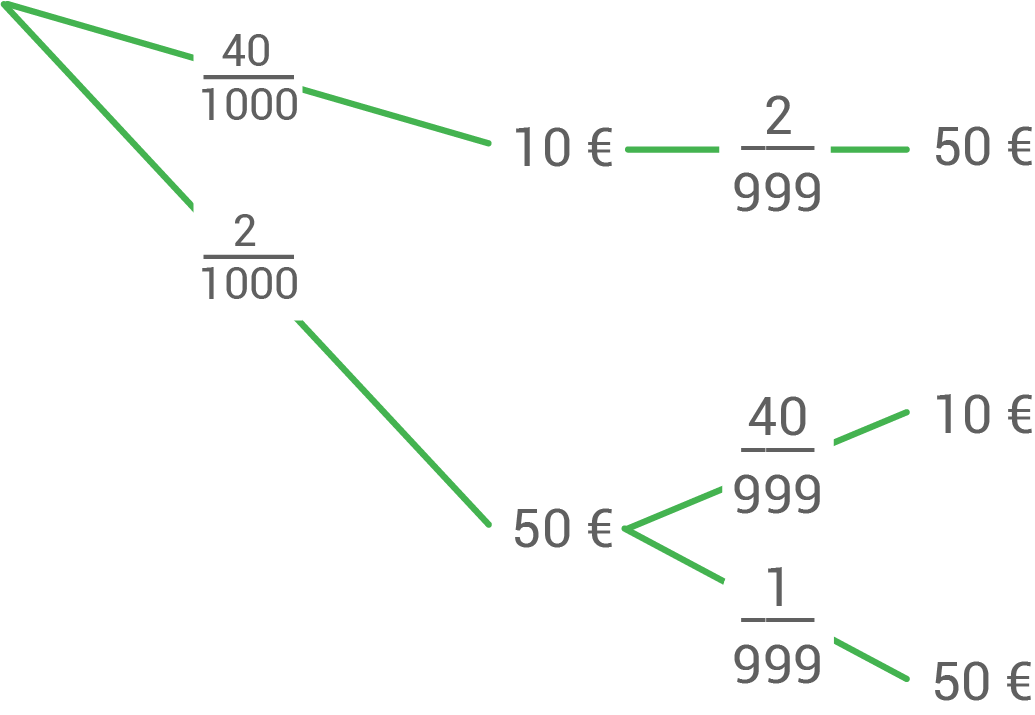
Der Gewinn einer Tombola kommt dem Schutz des Regenwaldes zugute. Auf den Losen steht jeweils genau eine der Zahlen von 1 bis 1000. Auf einem Plakat steht:

Die Zufallsvariable $X$ gibt den auszuzahlenden Betrag in Euro an.

Stelle die Wahrscheinlichkeitsverteilung von $X$ in einer Tabelle dar.

(4 BE)

Berechne die Wahrscheinlichkeit folgender Ereignisse:

A: = „Beim Ziehen eines Loses gewinnt man einen Preis.“

B: = „Man gewinnt mindestens 60 Euro, wenn man nacheinander zwei Lose zieht.“

(4 BE)

Gegeben ist die Funktion $k$ mit $k(x)=x^2+4x+1 \,\,(x \in \mathbb{R}).$

Der Graph von $k$ entsteht durch Verschiebung des Graphen der Funktion $f$ mit $f(x)=x^2.$
Beschreibe diese Verschiebung.

(2 BE)

Die Gerade $g$ verläuft durch die Punkte $P(1|3)$ und $Q(4|9).$
Berechne die Koordinaten der Schnittpunkte des Graphen von $k$ mit der Geraden $g.$

(4 BE)

Gegeben ist die Funktion $h$ mit der Gleichung $h(x)= -(x+2)^4+t\,\, (t, \,\,x\in \mathbb{R}).$ Ermittle die Anzahl der gemeinsamen Punkte der Graphen der Funktionen $k$ und $h$ in Abhängigkeit von $t.$
Bestimme den Wert von $t$ so, dass die Funktionen $k$ und $h$ dieselben Nullstellen haben.

(6 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$\color{#ffffff}{X}$	$0$	$1$	$10$	$50$
$\color{#ffffff}{P(X)}$	$\dfrac{858}{1000}$	$\dfrac{100}{1000}$	$\dfrac{40}{1000}$	$\dfrac{2}{1000}$

$\begin{array}[t]{rll} P(A)&=&\dfrac{100}{1000}+\dfrac{40}{1000}+\dfrac{2}{1000} \\[5pt] &=& \dfrac{142}{1000} \\[5pt] &=& 0,142 \end{array}$

Im folgenden Baumdiagramm sind nur die Pfade eingetragen, bei denen der Gewinn mindestens 60 € beträgt.

Rechenweg anzeigen

$P(B) \approx 0,000162$

Alternative 1: Rechnerische Lösung mit quadratischer Ergänzung

$\begin{array}[t]{rll} k(x)&=&x^2+4x+1 \\[5pt] &=& x^2+4x+\left(\dfrac{4}{2}\right)^2-\left(\dfrac{4}{2}\right)^2+1 \\[5pt] &=&(x+2)^2-3 \end{array}$

$\Rightarrow S(-2|-3)$

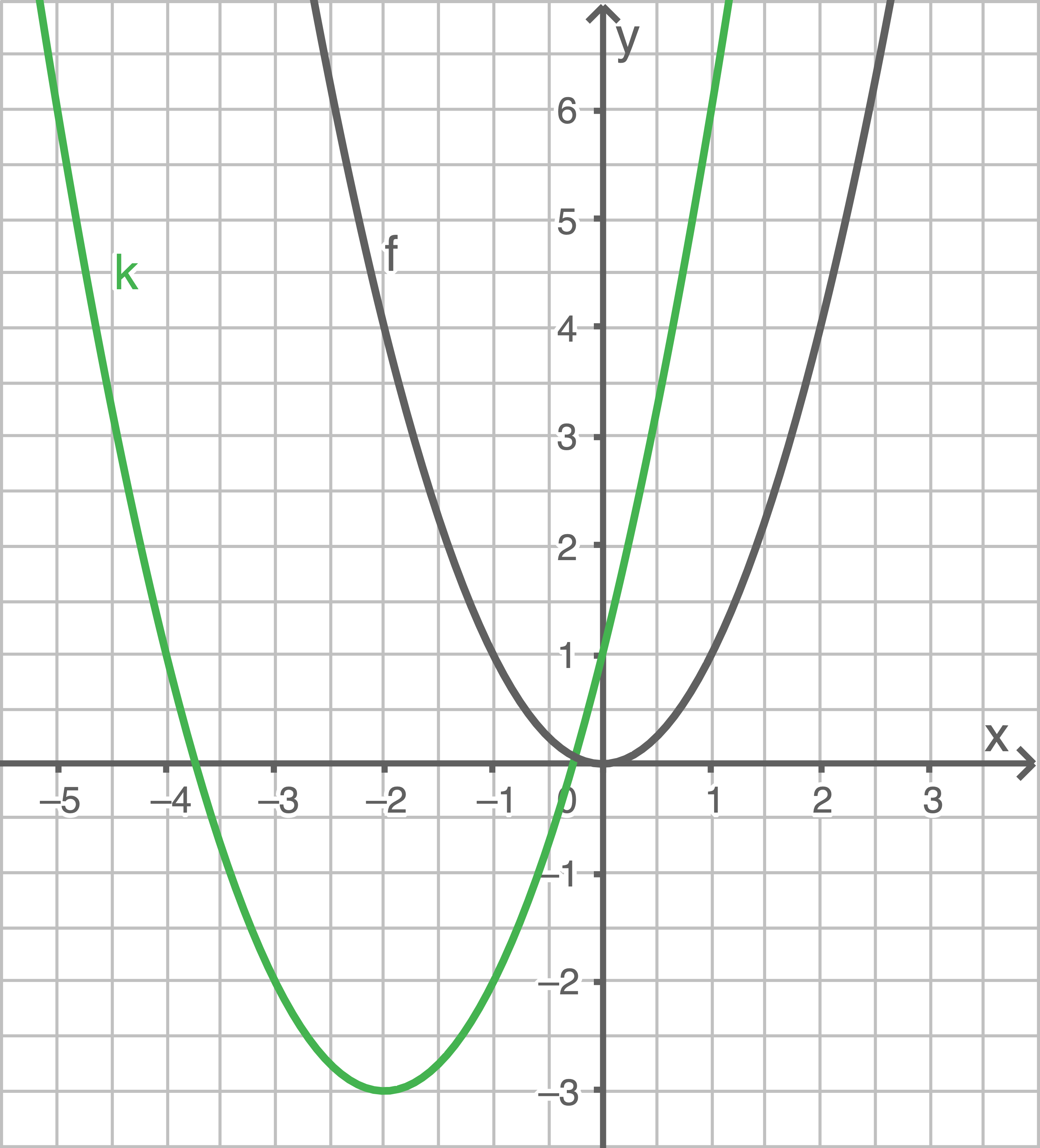
Verschiebung der Funktion $f$ um zwei Einheiten in negative $x$ -Richtung
Verschiebung der Funktion $f$ um drei Einheiten in negative $y$ -Richtung

Alternative 2: Graphische Lösung mit dem CAS

Geradengleichung $g$ aufstellen

Allgemeine Form der Geradengleichung: $y=m\cdot x+b$

$\begin{array}{lrll} \text{I}\quad&3&=& 1\cdot m+b &\quad \scriptsize\mid\;\text{I}-\text{II}\\ \text{II}\quad&9&=&4\cdot m+b &\quad \\ \hline &-6&=&-3\cdot m &\quad \scriptsize\mid\;:{(-3)}\\ &2&=&m & \end{array}$

$m=2$ in $\text{I}$ einsetzen:

$\begin{array}[t]{rll} 3&=&1\cdot 2+b &\quad \scriptsize \mid\;-2 \\[5pt] 1&=& b \end{array}$

Insgesamt folgt $g(x)=2x+1.$

2. Schritt: $k(x)=g(x)$ setzen

$x^2+4x+1 =2x+1$

Der CAS liefert $x_1=0$ und $x_2=-2.$

$x_1=0$ in $g(x)$ einsetzen

$\begin{array}[t]{rll} y_1&=&2\cdot 0+1 \\[5pt] y_1&=&1 \end{array}$

$x_2=-2$ in $g(x)$ einsetzen

$\begin{array}[t]{rll} y_2&=&2\cdot(-2)+1 \\[5pt] y_2&=&-3 \end{array}$

Es ergeben sich die Schnittpunkte $S_1(0\mid1)$ und $S_2(-2\mid-3).$

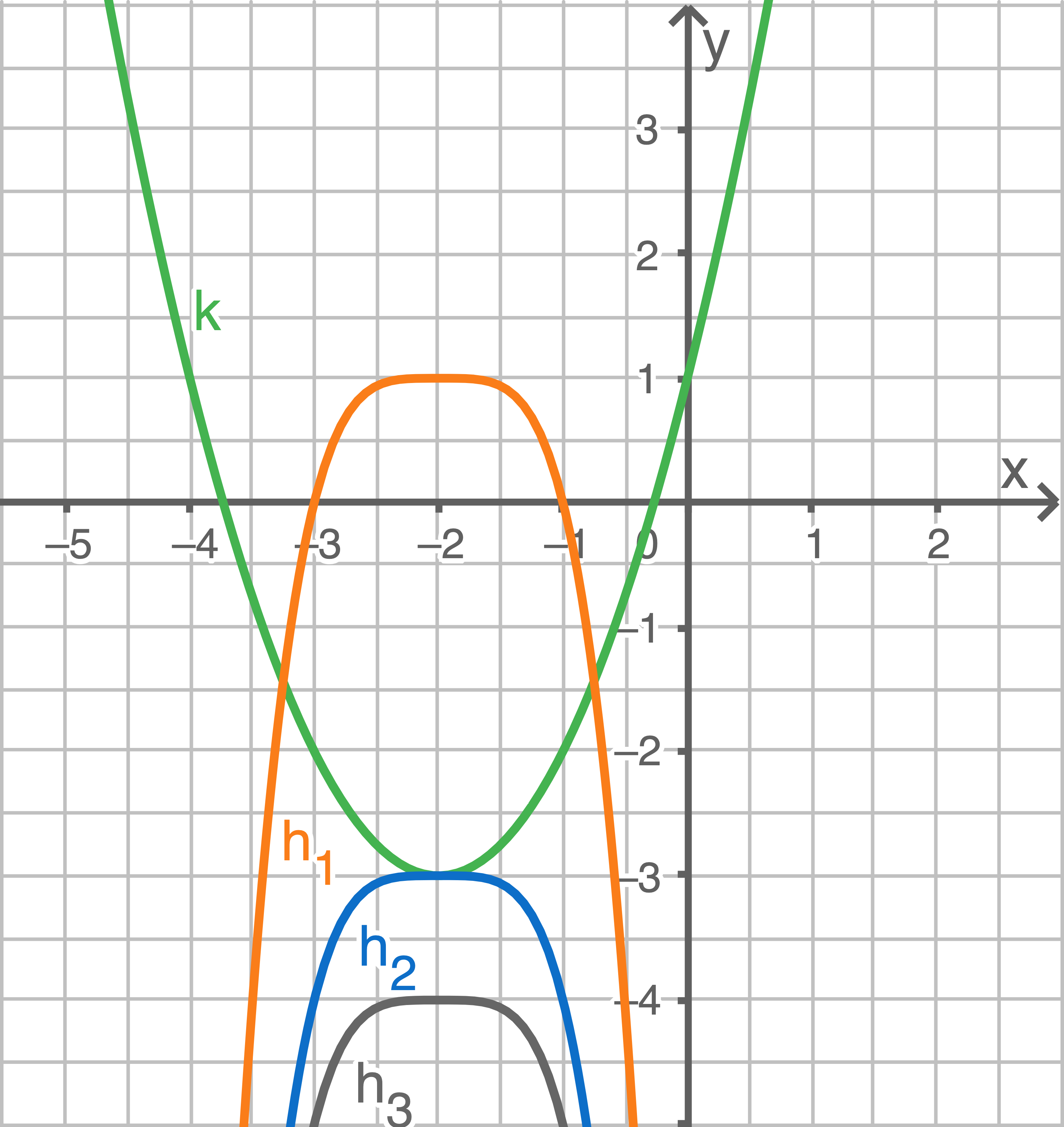
Anzahl der gemeinsamen Punkte ermitteln

Der Graph der Funktion $k$ hat den Scheitelpunkt $S(-2|-3)$ (siehe Lösung der Aufgabe 2 a).

Damit folgt: Die Graphen $k(x)$ und $h(x)$ haben

zwei gemeinsame Punkte für $t\gt-3$
einen gemeinsamen Punkt für $t=-3$
keine gemeinsamen Punkte für $t\lt-3$

Zur Veranschaulichung:

$h_1(x)=-(x+2)^4+1$
$h_2(x)=-(x+2)^4-3$
$h_3(x)=-(x+2)^4-4$

Wert von $\boldsymbol{t}$ bestimmen

Nullstellen der Funktion $k$ bestimmen

$x^2+4x+1=0$

Der Taschenrechner liefert $x_1=-2+\sqrt{3}$ und $x_2=-2-\sqrt{3}.$

$t$ bestimmen

$\begin{array}[t]{rll} h(-2+\sqrt{3})&=& 0 \\[5pt] -((-2+\sqrt{3})+2)^4+t&=&0 \\[5pt] -(\sqrt{3})^4+t&=&0 \\[5pt] -9+t&=&0 &\quad \scriptsize \mid\; +9\\[5pt] t&=&9 \\[5pt] \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?