Pflichtaufgabe 1 – Ohne Hilfsmittel
1.
Ermittle die Lösung des Gleichungssystems 
(2 BE)
2.
Gegeben sind die Funktionen 
und 
durch 
und 
Bestimme graphisch die Koordinaten der Schnittpunkte von und 
und durch und
Bestimme graphisch die Koordinaten der Schnittpunkte von und
(3 BE)
3.
Gib die Gleichung einer Funktion an, deren Graph für 
monoton fallend und für 
monoton steigend ist.
monoton fallend und für monoton steigend ist.
(1 BE)
4.
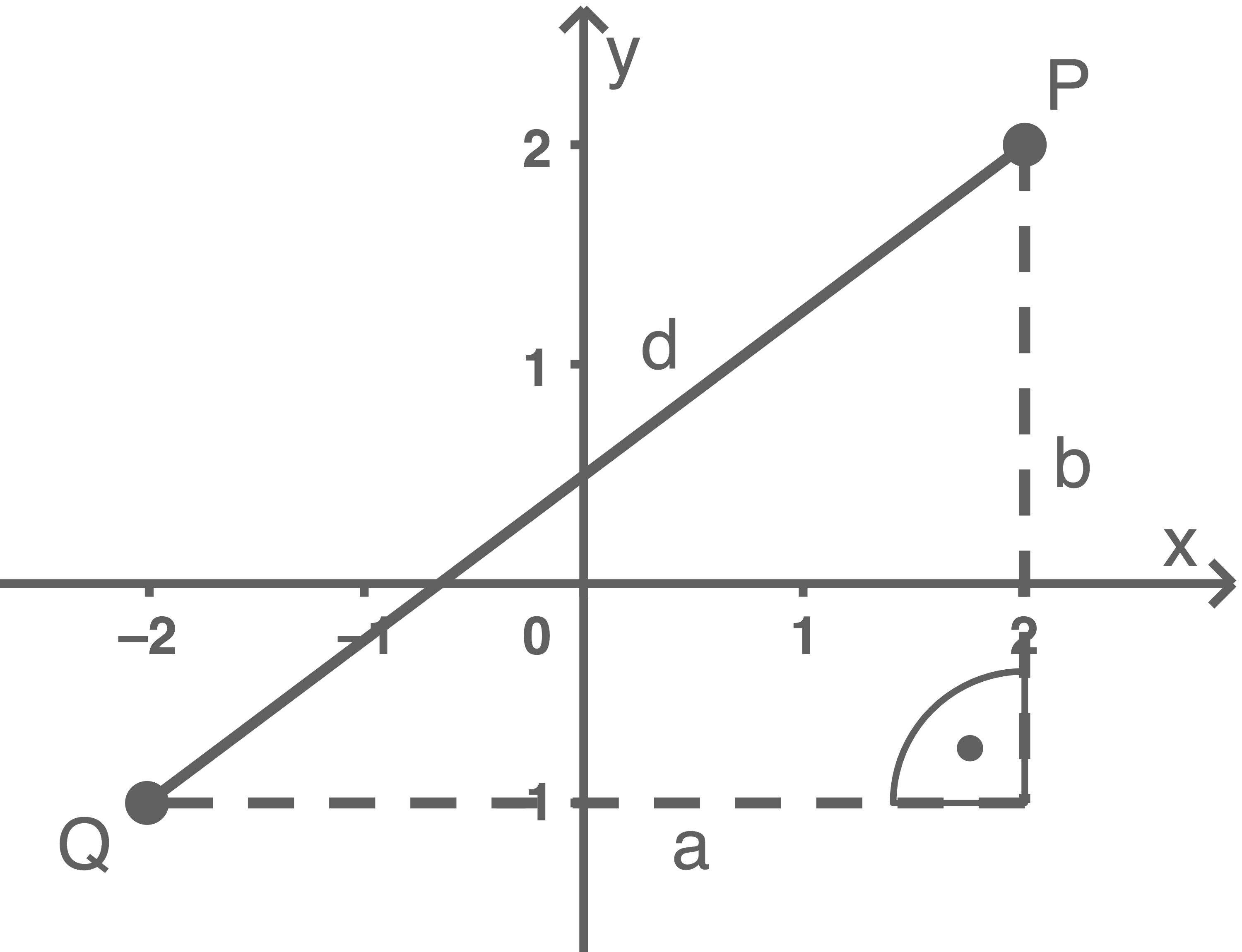
Berechne den Abstand der Punkte 
und 
.
und .
(2 BE)
5.
Gib ein Zufallsexperiment mit den zwei Eigenschaften an:
- Es gibt genau zwei mögliche Ergebnisse.
- Die Wahrscheinlichkeit eines der beiden Ergebnisse beträgt
.
(1 BE)
6.
Eine Münze wird einmal geworfen. Der Versuch wird 400-mal wiederholt. Die relativen Häufigkeiten für Wappen wurden in Abhängigkeit von der Anzahl der Versuche mit einem Computerprogramm graphisch dargestellt.
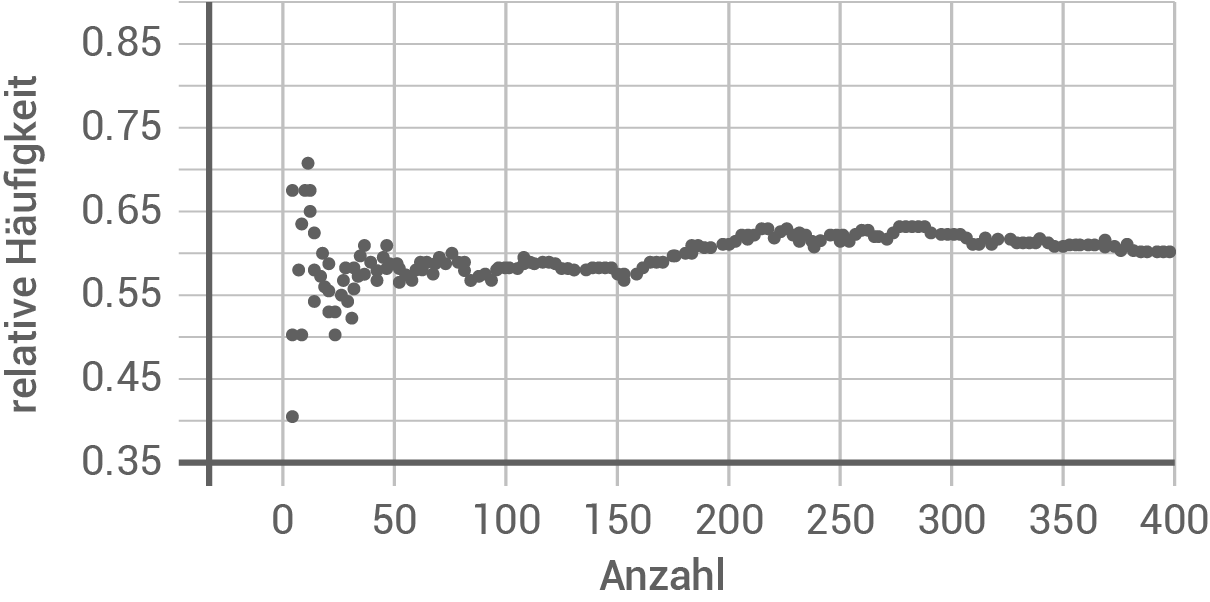Entscheide, ob mit einer idealen Münze geworfen wurde. Begründe deine Entscheidung.
(1 BE)
1.
Da die zweite Gleichung bereits nach 
umgestellt ist, bietet sich das Einsetzungsverfahren an. Andere Verfahren führen jedoch zur gleichen Lösung.
in 
![\(\begin{array}[t]{rll}
6&=& 2x+3\cdot (x+7) \\[5pt]
6&=& 2x+3x+21\quad \scriptsize \mid\; -21\\[5pt]
-15&=& 5x \quad \scriptsize \mid\; :5\\[5pt]
-3&=& x
\end{array}\)](https://www.schullv.de/resources/formulas/31386c7993f0b75a5b123a2213481e7ccf7fa2a7075f1b6691b520729f3393a7_light.svg)
in einsetzen:
Das Gleichungssystem hat die Lösung und 
umgestellt ist, bietet sich das Einsetzungsverfahren an. Andere Verfahren führen jedoch zur gleichen Lösung.
in
in einsetzen:
Das Gleichungssystem hat die Lösung und
2.
und 
ablesen.
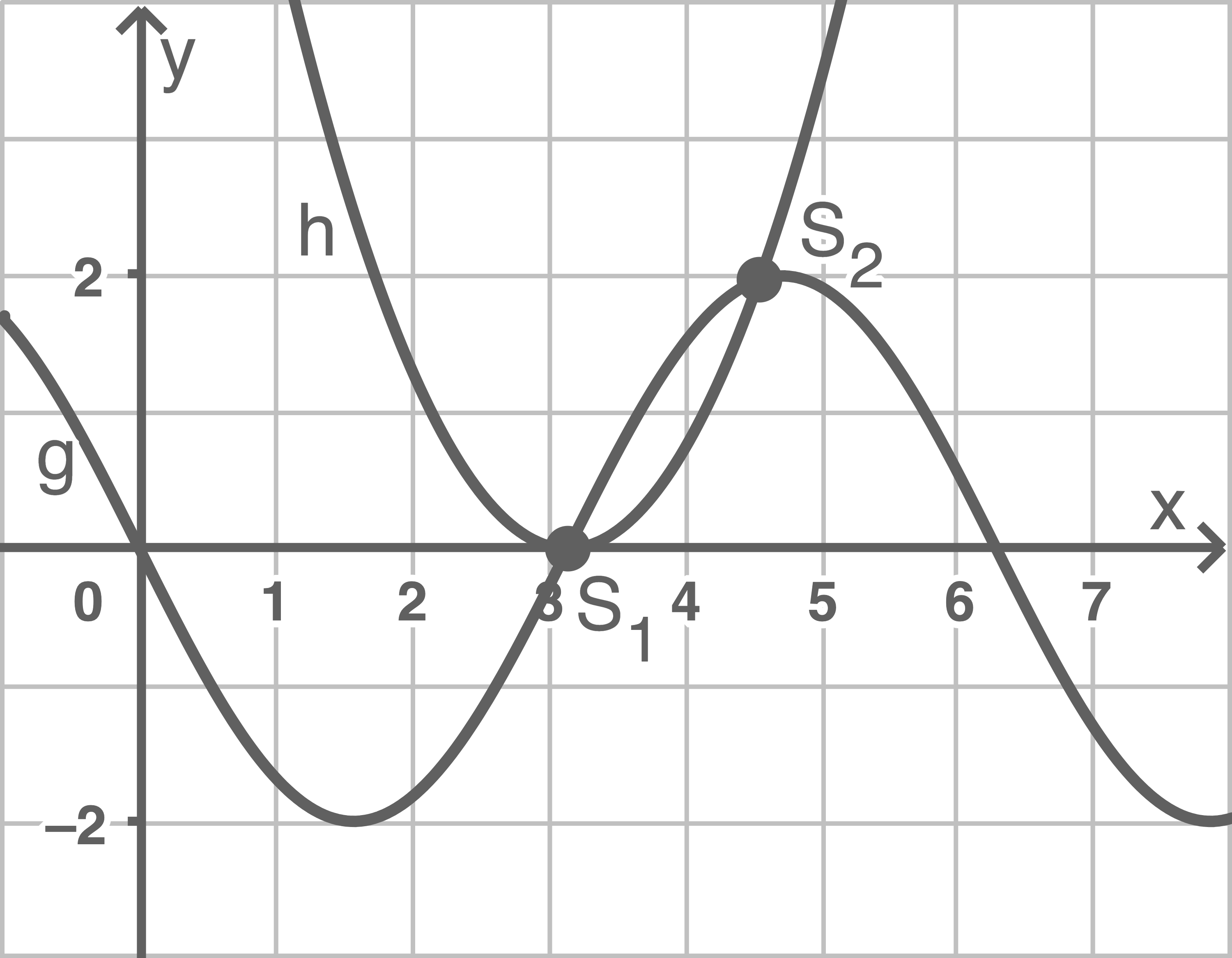
3.
Geeignet ist der Graph einer quadratischen Funktion, da sich hier das monotone Verhalten des Graphen am Scheitelpunkt ändert. In diesem Fall muss die Parabel nach oben geöffnet sein und ihren Scheitelpunkt an der Stelle 
haben. Das ist beispielsweise für die folgende Funktion der Fall:
haben. Das ist beispielsweise für die folgende Funktion der Fall:
4.
Der Abstand 
der Punkte lässt sich mit dem Satz des Pythagoras berechnen:
![\(\begin{array}[t]{rll}
d^2&=& a^2+b^2 \\[5pt]
d^2&=& (x_P-x_Q)^2+(y_P-y_Q)^2 \\[5pt]
d^2&=& (2-(-2))^2+(2-(-1))^2 \\[5pt]
d^2&=& 4^2+3^2 \\[5pt]
d^2&=& 25 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
d&=& 5
\end{array}\)](https://www.schullv.de/resources/formulas/683a922a0d5d020e3f052f1b1e7f2970994894f67c08869ac4a80a90fc75e150_light.svg)
Der Abstand der beiden Punkte beträgt 5 LE.
der Punkte lässt sich mit dem Satz des Pythagoras berechnen:
5.
Das Zufallsexperiment muss zwei Eigenschaften erfüllen:
.
- Es gibt genau zwei Ergebnisse
- Die Wahrscheinlichkeit eines der beiden Ergebnisse beträgt 0,8
.
6.
Bei einer idealen Münze sind die Ergebnisse Zahl und Wappen gleich wahrscheinlich. Nach einer großen Anzahl an Wiederholungen sollte die relative Häufigkeit für eines der Ergebnisse sich um 
herum verteilen.
Hier liegt die relative Häufigkeit von Wappen nach 400 Würfen bei etwa 
Daher ist davon auszugehen, dass es keine ideale Münze ist.
herum verteilen.
Hier liegt die relative Häufigkeit von Wappen nach 400 Würfen bei etwa Daher ist davon auszugehen, dass es keine ideale Münze ist.