Wahlaufgabe 2
1.
Dargestellt ist der Grundriss eines ebenen Grundstücks, welches die Form eines Viereckes hat.
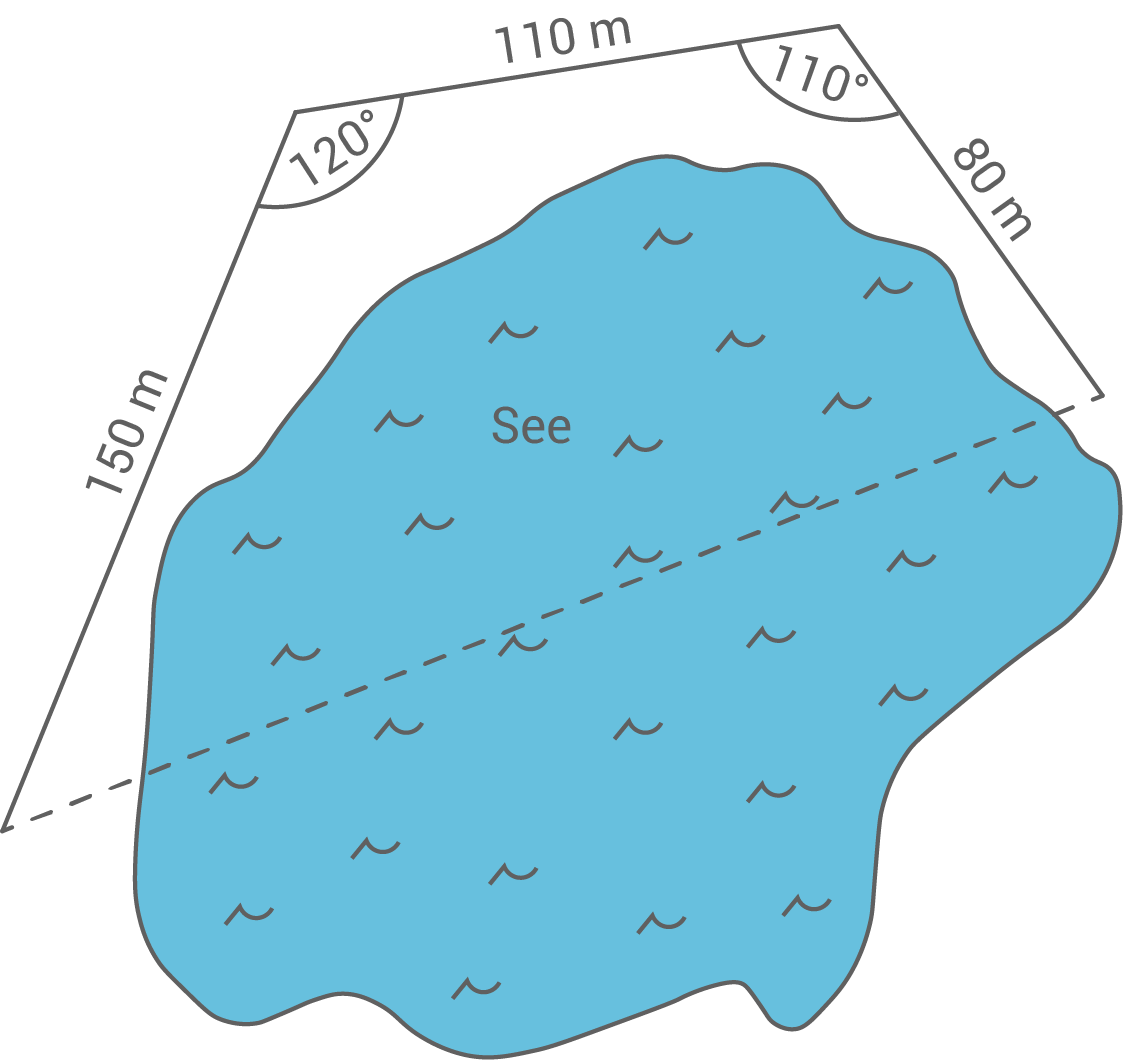
Skizze nicht maßstäblich
a)
Die Länge einer Grundstücksgrenze wurde bei der Vermessung nicht ermittelt. Berechne die Länge dieser Grundstücksgrenze.
(5 BE)
b)
Überprüfe deine Berechnungen aus Teilaufgabe a) durch eine maßstabsgerechte Zeichnung. Gib den gewählten Maßstab an.
(3 BE)
2.
Bei einem Gewitter entstehen Blitz und Donner zur gleichen Zeit am gleichen Ort. Der Schall legt in 3 Sekunden etwa eine Strecke von 1 km zurück. Das Licht ist so schnell, dass man es nahezu im Moment der Entstehung des Blitzes sieht.
a)
Paul sieht einen Blitz und hört nach 20 Sekunden den Donner.
Berechne die Entfernung des Blitzes von Pauls Standort.
Berechne die Entfernung des Blitzes von Pauls Standort.
(2 BE)
b)
Ein Blitz schlägt 3,5 km von einem Badesee entfernt ein.
Berechne die Zeit, die vergeht, bis die Badegäste den Donner hören.
Berechne die Zeit, die vergeht, bis die Badegäste den Donner hören.
(2 BE)
3.
Die Punkte 
und 
liegen auf dem Graphen der Exponentialfunktion 
mit 
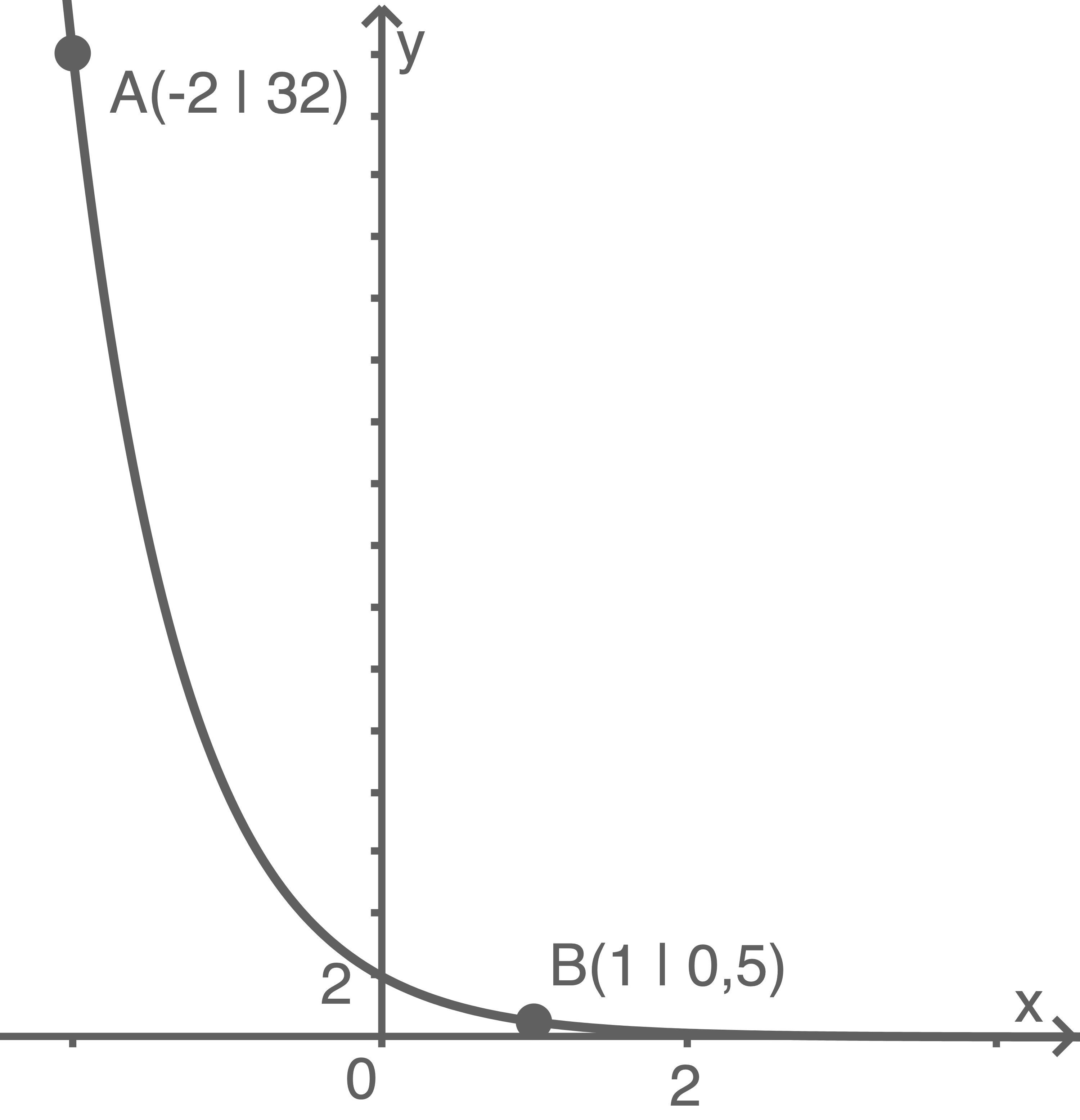
a)
Nenne zwei Eigenschaften von 
(2 BE)
b)
Bestimme eine Gleichung von
(2 BE)
c)
Ermittle die Gleichungen zweier Funktionen 
und 
deren Graphen ebenfalls durch die Punkte 
und 
verlaufen.
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
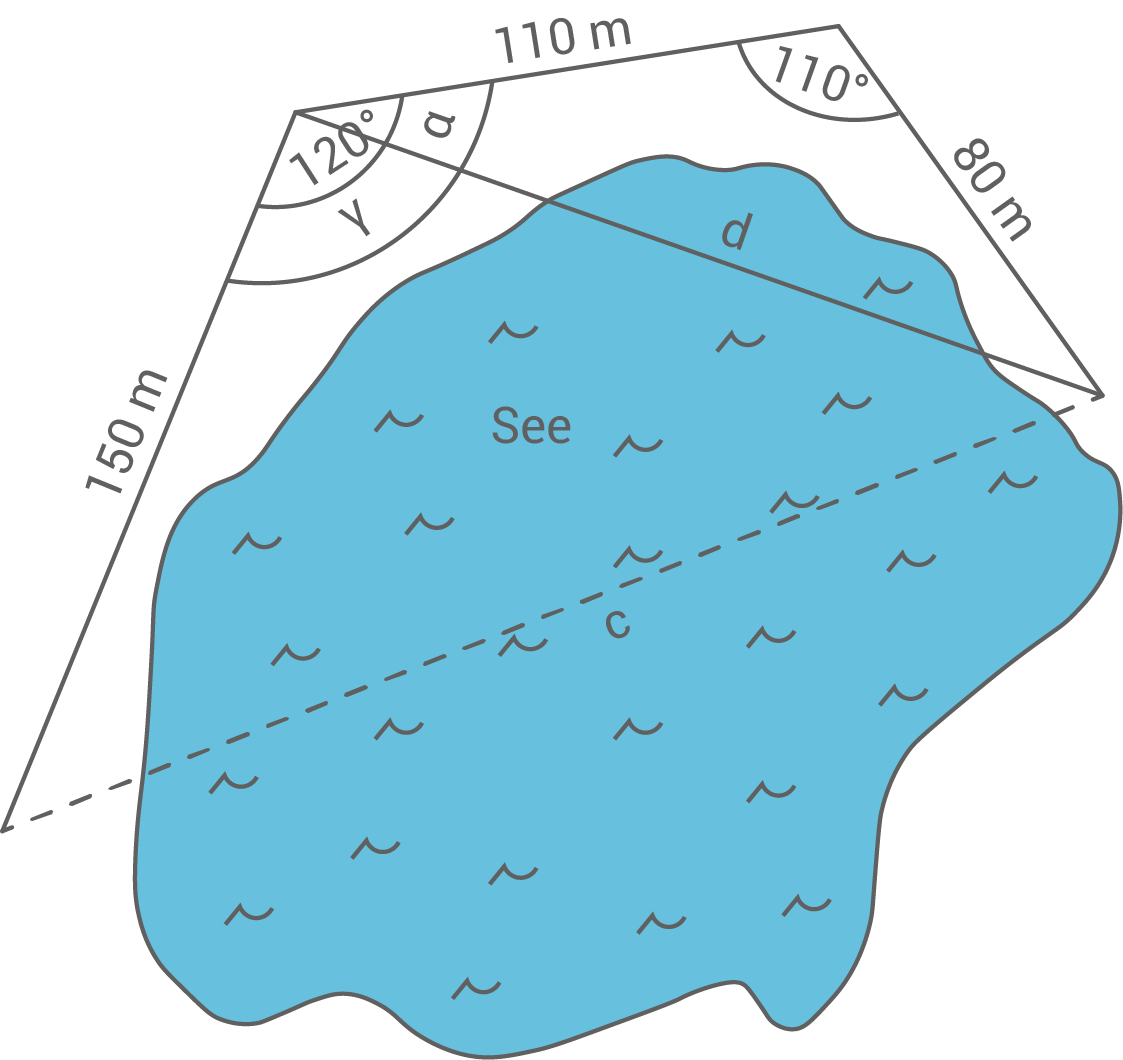
Skizze (nicht maßstabsgetreu)
b)
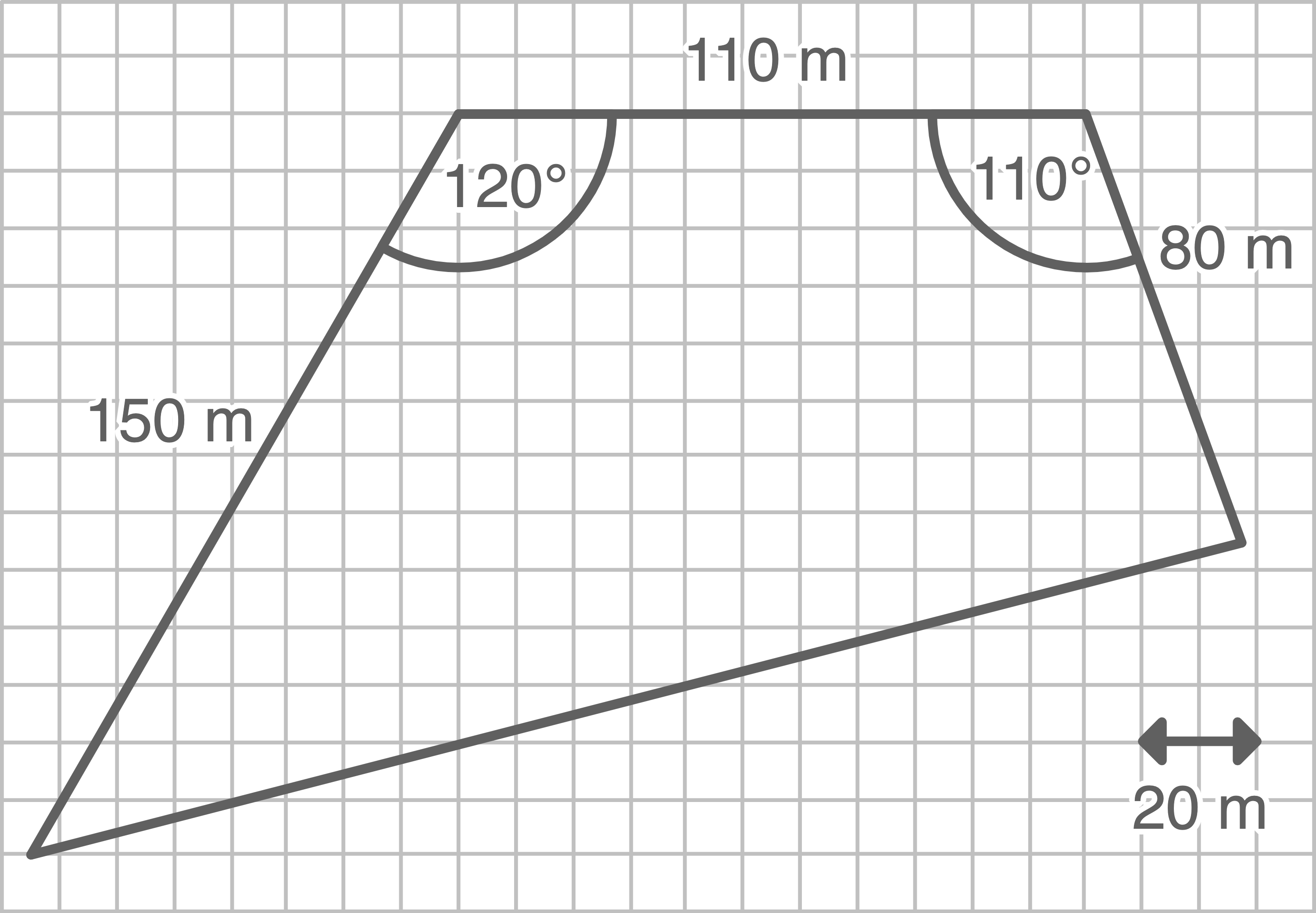
2.
a)
b)
3.
a)
- Die Funktion
- Die Funktion
b)
Da der Graph die 
-Achse im Punkt 
schneidet, muss gelten:
![\(\begin{array}[t]{rll}
f(0)&=& 2 \\[5pt]
a\cdot b^0&=& 2 \\[5pt]
a&=&2
\end{array}\)](https://mathjax.schullv.de/69149ba58e30a89fd598fa33adcd554bcdf7b6125de2b9c9ffadac2b07ea512a?color=5a5a5a)
Die Funktionsgleichung ist also von der Form 
Einsetzen der Koordinaten des Punktes 
liefert:
![\(\begin{array}[t]{rll}
0,5&=& 2\cdot b^1 &\quad \scriptsize \mid\; :2 \\[5pt]
0,25&=& b
\end{array}\)](https://mathjax.schullv.de/58c91109c43086ae25cd5687a8d2de9f87c817aac3c5bff62b8a50a217253754?color=5a5a5a)
Insgesamt gilt 
c)
Als erster Ansatz kann eine lineare Funktion der Form 
gewählt werden. Einsetzen der Koordinaten der Punkte und liefert die folgenden Gleichungen:
Umstellen der Gleichung 
liefert 
Durch Einsetzen in 
folgt:
![\(\begin{array}[t]{rll}
32&=& -2m+(0,5-m)\\[5pt]
32&=& -3m+0,5 \quad \scriptsize \mid\; -0,5\\[5pt]
31,5&=& -3m \quad \scriptsize \mid\; :(-3)\\[5pt]
-10,5&=& m
\end{array}\)](https://mathjax.schullv.de/c067bcc268e2e7755d7ddf506b623efc2b882f0e839fb812b082c22eafb4d650?color=5a5a5a)
Daraus folgt 
Eine mögliche Funktion, deren Graph durch und verläuft, ist die Funktion 
Als zweiter Ansatz kann eine quadratische Funktion mit 
gewählt werden. Einsetzen der Koordinaten beider Punkte liefert die folgenden Gleichungen:
![\(\begin{array}[t]{rll}
\text{I} \quad &32&=& (-2)^2+p\cdot (-2)+q \\[5pt]
&32&=& 4-2p+q
\end{array}\)](https://mathjax.schullv.de/fb705db725adb5a6a0bab9f77881a5620361821532b5c6bbc26c49b2baa41c0b?color=5a5a5a)
![\(\begin{array}[t]{rll}
\text{II} \quad& 0,5&=& 1^2+p\cdot 1+q \\[5pt]
&0,5&=& 1+p+q \quad \scriptsize \mid\;-1 \\[5pt]
&-0,5&=& p+q \quad \scriptsize \mid\;-q \\[5pt]
&-0,5-q&=& p \\[5pt]
\end{array}\)](https://mathjax.schullv.de/8ff34ae9096dbae809adec31726fc4b14c2cbe39f3ec08a5f13b6064c4a811dc?color=5a5a5a)
Einsetzen von in liefert:
![\(\begin{array}[t]{rll}
32&=& 4-2\cdot (-0,5-q)+q \\[5pt]
32&=& 4+1+2q+q \\[5pt]
32&=& 5+3q \quad \scriptsize \mid\;-5 \\[5pt]
27&=& 3q \quad \scriptsize \mid\; :3 \\[5pt]
9&=& q
\end{array}\)](https://mathjax.schullv.de/bd84cbfad252a980d98c387cc86933ffc8259ea3e27e1079a2b6fb17d19505ef?color=5a5a5a)
Daraus folgt 
Eine zweite mögliche Gleichung lautet 