Pflichtaufgabe 2 – Mit Hilfsmitteln

Die Wasserhyazinthe kann sich unter idealen Bedingungen äußerst stark vermehren. Zu Beobachtungsbeginn werden etwa 20 Quadratmeter eines 72 Hektar großen Sees durch Wasserhyazinthen bedeckt. Die bedeckte Fläche nimmt pro Woche um 30 % zu.

Ermittle eine Funktionsgleichung, mit der sich das Pflanzenwachstum mathematisch beschreiben lässt.

(2 BE)

Gib den Flächeninhalt der nach vier Wochen bedeckten Wasseroberfläche an.

(1 BE)

Berechne die Anzahl der Tage, nach denen der See vollständig bedeckt ist.

(2 BE)

Gib eine Grenze der verwendeten mathematischen Modellierung an.

(1 BE)

In einem rechtwinkligen Koordinatensystem sind die Punkte $A(0\mid 2),$ $B(-1\mid 0)$ und $C(3\mid -4)$ gegeben.

Berechne die Größe eines Innenwinkels des Dreiecks $ABC.$

(3 BE)

Die Punkte $A,$ $B,$ $C$ und $D$ bilden in dieser Reihenfolge ein Drachenviereck. Ermittle die Gleichung der Geraden, auf der die Diagonale $\overline{BD}$ liegt.

(3 BE)

Anna und Marcel spielen mit zwei unterscheidbaren Münzen nach nebenstehender Anweisung.
Sie haben eine ideale Münze und eine gezinkte Münze, bei der Wappen mit einer Wahrscheinlichkeit von 70 % fällt.
Entscheide, in welcher Reihenfolge die Münzen geworfen werden sollten, damit die Wahrscheinlichkeit für einen Gewinn am größten ist. Begründe deine Entscheidung.

Anweisung

Der Spieler wählt eine Münze und wirft diese.
In Abhängigkeit vom Ergebnis wählt der Spieler erneut eine Münze und wirft diese.

Gewonnen hat der Spieler, der genau einmal Wappen und einmal Zahl geworfen hat.

(3 BE)

Bei dem beschriebenen Wachstum handelt es sich um exponentielles Wachstum. Die Funktionsgleichung hat also die Form $f(x) = b\cdot a^x.$

Der Anfangsbestand in Quadratmetern ist laut Aufgabenstellung gegeben durch $b = 20.$

Die bedeckte Fläche nimmt pro Woche um 30 % zu. Der Wachstumsfaktor $a$ ist also $a=1+0,3 = 1,3.$

Die bedeckte Fläche des Sees in Quadratmetern $x$ Wochen nach Beobachtungsbeginn kann also mit folgender Gleichung beschrieben werden:

$f(x) = 20\cdot 1,3^x$

$\begin{array}[t]{rll} f(4) &=& 20\cdot 1,3^4 \\[5pt] &\approx& 57,1 \end{array}$

Vier Wochen nach Beobachtungsbeginn sind ungefähr $57\,\text{m}^2$ des Sees durch Wasserhyazinthen bedeckt.

$72\,\text{ha} = 720\,000\,\text{m}^2$

Gesucht ist die Lösung der Gleichung $f(x)= 720\,000.$

Der Taschenrechner liefert $x\approx 40.$

Nach ca. 40 Wochen, also 280 Tagen, ist der See vollständig bedeckt.

Nach der Modellierung wächst die von der Pflanze bedeckte Fläche des Sees bis ins Unendliche. Der See hat aber nur eine begrenzte Größe von $72\,\text{ha}.$ Die bedeckte Fläche würde nach der Modellierung also irgendwann die Größe des Sees überschreiten, was im Sachzusammenhang aber nicht möglich ist.

Über die Koordinatenangaben der Eckpunkte können die Seitenlängen des Dreiecks berechnet werden.

$\begin{array}[t]{rll} c=\overline{AB}&=& \sqrt{(y_B-y_A)^2 + (x_B-x_A)^2} \\[5pt] &=& \sqrt{(0-2)^2 + (-1-0)^2 } \\[5pt] &=& \sqrt{5} \\[10pt] b=\overline{AC} &=& \sqrt{(y_C-y_A)^2 + (x_C-x_A)^2} \\[5pt] &=& \sqrt{(-4-2)^2 + (3-0)^2} \\[5pt] &=& \sqrt{45} \\[10pt] a=\overline{BC} &=& \sqrt{(y_C-y_B)^2 + (x_C-x_B)^2} \\[5pt] &=& \sqrt{(-4-0)^2 + (3-(-1))^2} \\[5pt] &=& \sqrt{32} \\[10pt] \end{array}$

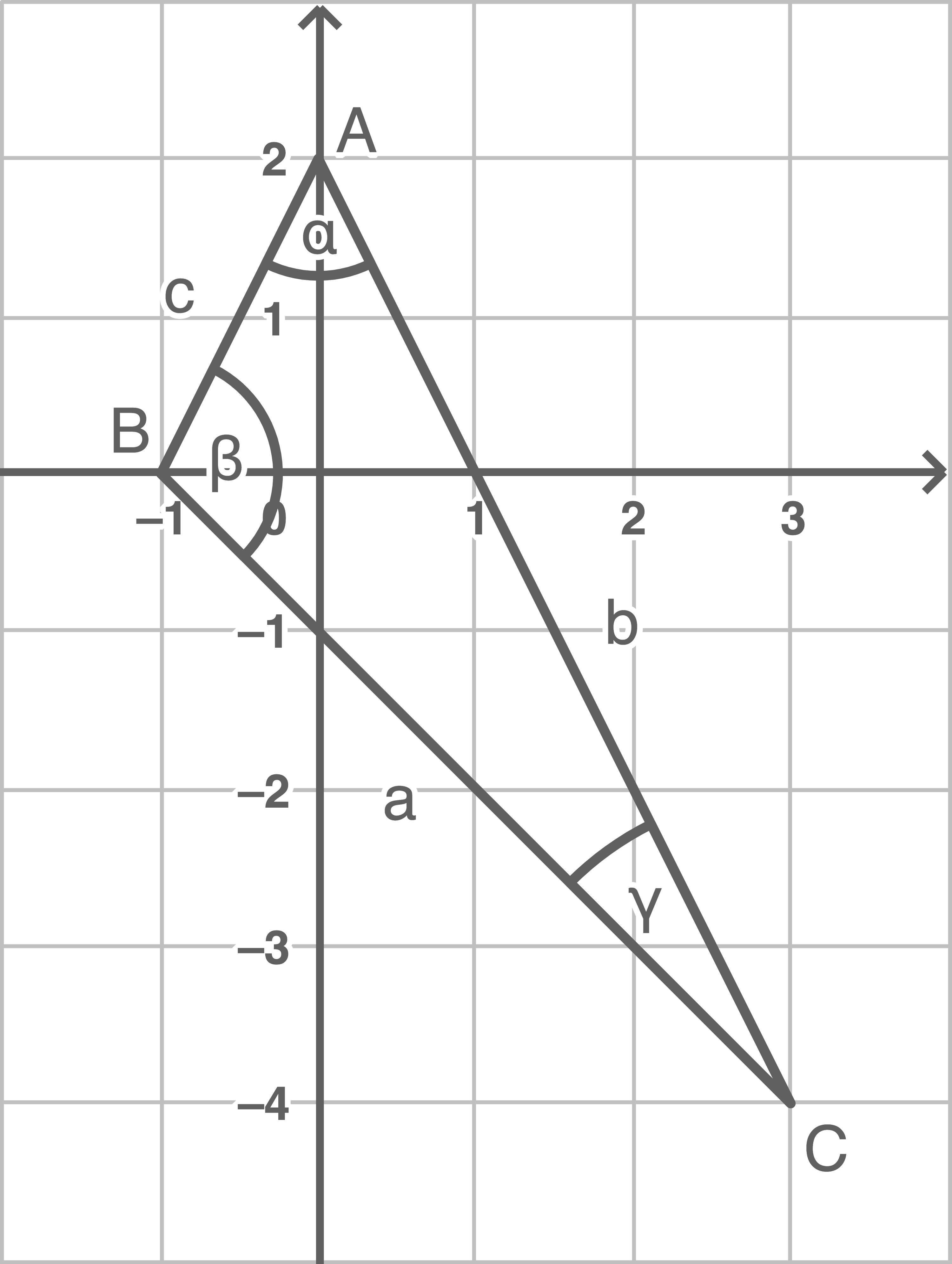Mit dem Kosinussatz können nun alle Innenwinkel berechnet werden. Im Folgenden sind die Rechnungen für alle drei Winkel aufgeführt, gefragt ist jedoch nur ein Winkel. Die jeweiligen Gleichungen können mit dem Taschenrechner gelöst werden.

$\begin{array}[t]{rll} a^2&=& b^2 +c^2 -2bc\cdot \cos \alpha \\[5pt] \sqrt{32}^2&=& \sqrt{45}^2 + \sqrt{5}^2 -2\cdot \sqrt{45} \cdot \sqrt{5}\cdot \cos \alpha \\[5pt] 53,1^{\circ}&\approx& \alpha \end{array}$

$\begin{array}[t]{rll} b^2&=& a^2 +c^2 -2ac\cdot \cos \beta \\[5pt] \sqrt{45}^2&=& \sqrt{32}^2 + \sqrt{5}^2 -2\cdot \sqrt{32} \cdot \sqrt{5}\cdot \cos \beta \\[5pt] 108,4^{\circ}&\approx& \beta \end{array}$

$\begin{array}[t]{rll} c^2&=& a^2 +b^2 -2ab\cdot \cos \gamma \\[5pt] \sqrt{5}^2&=& \sqrt{32}^2 + \sqrt{45}^2 -2\cdot \sqrt{32} \cdot \sqrt{45}\cdot \cos \gamma \\[5pt] 18,4^{\circ}&\approx& \gamma \end{array}$

Zunächst können die Punkte zur besseren Vorstellung in ein Koordinatensystem eingezeichnet werden. Der Punkt $D$ wird so ergänzt, dass ein Drachenviereck entsteht.

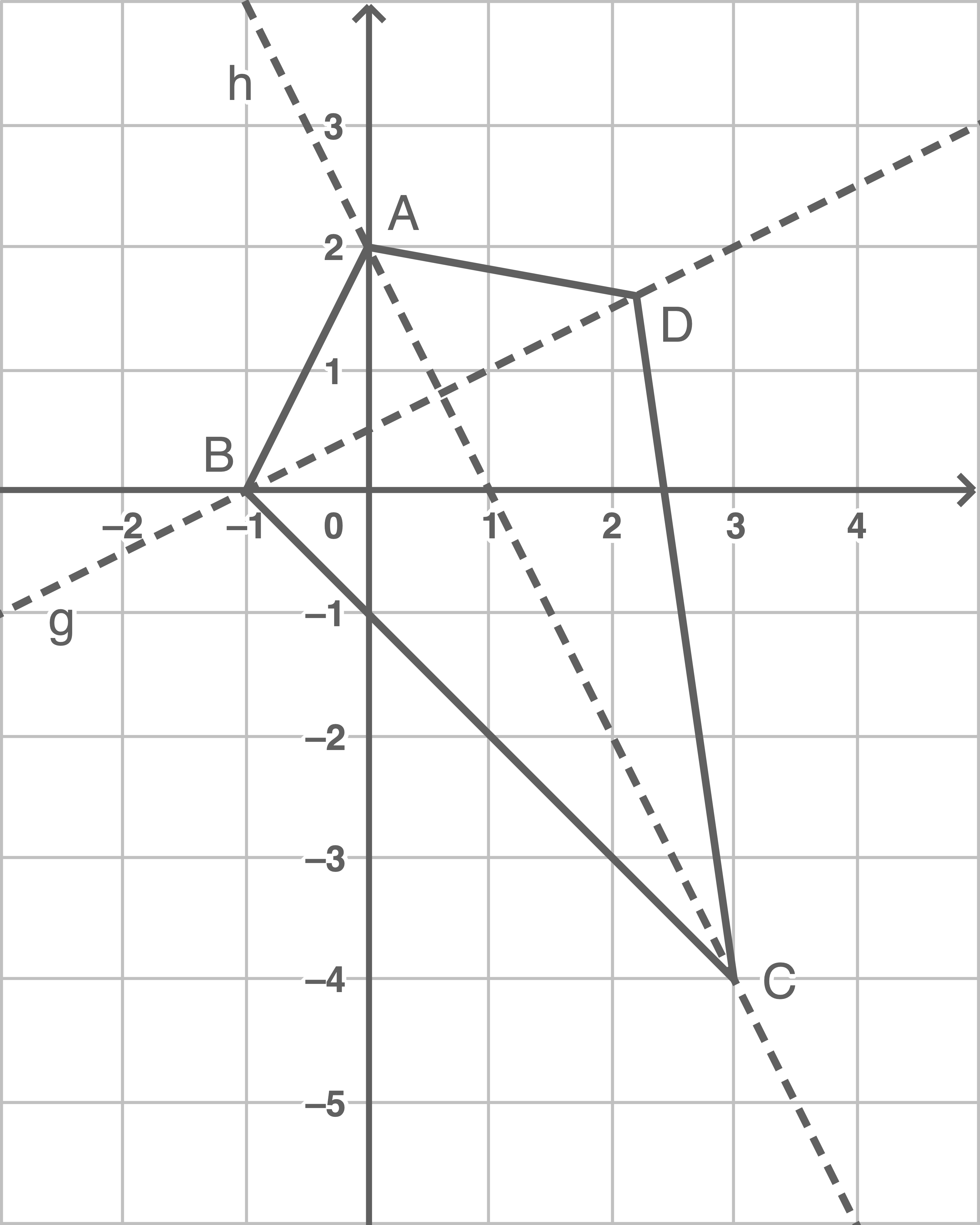
Die Gerade $g$ durch $B$ und $D$ muss in einem Drachenviereck rechtwinklig zur Geraden $h$ durch die Punkte $A$ und $C$ liegen. Mithilfe der Steigung von $h$ kann daher die Steigung von $g$ ermittelt werden. Die Steigung von $h$ kann mithilfe des Differenzenquotienten berechnet werden.

$\begin{array}[t]{rll} m_h&=& \dfrac{y_C-y_A}{x_C-x_A} \\[5pt] &=& \dfrac{-4-2}{3-0} \\[5pt] &=& \dfrac{-6}{3} \\[5pt] &=& -2 \end{array}$

Da $g$ senkrecht zu $h$ verlaufen muss, gilt für die beiden Steigungen folgender Zusammenhang:

$\begin{array}[t]{rll} m_g\cdot m_h&=& -1 \\[5pt] m_g\cdot(-2)&=& -1 &\quad \scriptsize \mid\;:-2 \\[5pt] m_g&=& 0,5 \end{array}$

Die Funktionsgleichung der Geraden durch $B$ und $D$ hat also die Form $y= 0,5\cdot x +n.$ Der $y$ -Achsenabschnitt $n$ kann durch Einsetzen der Koordinaten von $B$ berechnet werden:

$\begin{array}[t]{rll} y&=& 0,5\cdot x +n \quad \scriptsize \mid\;B(-1\mid 0) \\[5pt] 0&=& 0,5\cdot (-1) + n \quad \scriptsize \mid\;+0,5 \\[5pt] 0,5&=& n \end{array}$

Die Diagonale $\overline{BD}$ liegt also auf der Geraden mit der Gleichung $y= 0,5\cdot x+0,5.$

Es gibt vier verschiedene Möglichkeiten, wie die Münzen geworfen werden können. Die Wahrscheinlichkeiten für einen Gewinn in den jeweiligen Fällen werden im Folgenden berechnet:

Möglichkeit 1.1: Erster und zweiter Wurf mit idealer Münze

1. Wurf	2. Wurf	Wahrscheinlichkeit
Wappen	Zahl	$0,5\cdot 0,5=0,25$
Zahl	Wappen	$0,5\cdot 0,5=0,25$

Möglichkeit 1.2: Erster Wurf mit idealer und zweiter Wurf mit gezinkter Münze

1. Wurf	2. Wurf	Wahrscheinlichkeit
Wappen	Zahl	$0,5\cdot 0,3=0,15$
Zahl	Wappen	$0,5\cdot 0,7=0,35$

Möglichkeit 2.1: Erster Wurf mit gezinkter und zweiter Wurf mit idealer Münze

1. Wurf	2. Wurf	Wahrscheinlichkeit
Wappen	Zahl	$0,7\cdot 0,5=0,35$
Zahl	Wappen	$0,3\cdot 0,5=0,15$

Möglichkeit 2.2: Erster und zweiter Wurf mit gezinkter Münze

1. Wurf	2. Wurf	Wahrscheinlichkeit
Wappen	Zahl	$0,7\cdot 0,3=0,21$
Zahl	Wappen	$0,3\cdot 0,7=0,21$

Um die Siegwahrscheinlichkeiten zu maximieren, ergeben sich je nach zuerst geworfener Münze folgende Strategien:

Möglichkeit 1: Erster Wurf mit idealer Münze

Wirft man im ersten Wurf Wappen, so bleibt man beim zweiten Wurf bei der idealen Münze. Wird im ersten Wurf Zahl geworfen, so ist die Siegwahrscheinlichkeit beim Wechsel auf die gezinkte Münze höher. Die Gesamtwahrscheinlichkeit bei Möglichkeit 1 ergibt sich damit zu:

$p_1=0,25+0,35=0,6$

Möglichkeit 2: Erster Wurf mit gezinkter Münze

Fällt im ersten Wurf Wappen, so wird im zweiten Wurf auf die ideale Münze gewechselt. Fällt dagegen zuerst Zahl, so ist die Gewinnwahrscheinlichkeit höher, wenn nochmal die gezinkte Münze geworfen wird. Die Gesamtwahrscheinlichkeit bei Möglichkeit 1 ergibt sich damit zu:

$p_2=0,35+0,21=0,51$

Die Gewinnwahrscheinlichkeit ist also am höchsten, wenn zuerst die ideale Münze geworfen wird. Für den zweiten Wurf wird die Münze abhängig vom Ergebnis wie unter Möglichkeit 1 beschrieben gewählt.