Wahlaufgabe 1
1.
Gegeben ist ein Rechteck 
mit 
und 
Für jede reelle Zahl
ist eine Funktion 
gegeben durch 
Für jede reelle Zahl
a)
Der Graph einer Funktion verläuft durch den Punkt 
Bestimme den Anstieg dieser Funktion.
Bestimme den Anstieg
(2 BE)
b)
Die Anzahl der Schnittpunkte des Graphen von mit den Seiten des Rechtecks ist abhängig vom Anstieg 
Ermittle mithilfe einer graphischen Darstellung den Einfluss des Anstiegs auf die Anzahl dieser Schnittpunkte.
Ermittle mithilfe einer graphischen Darstellung den Einfluss des Anstiegs
(5 BE)
2.
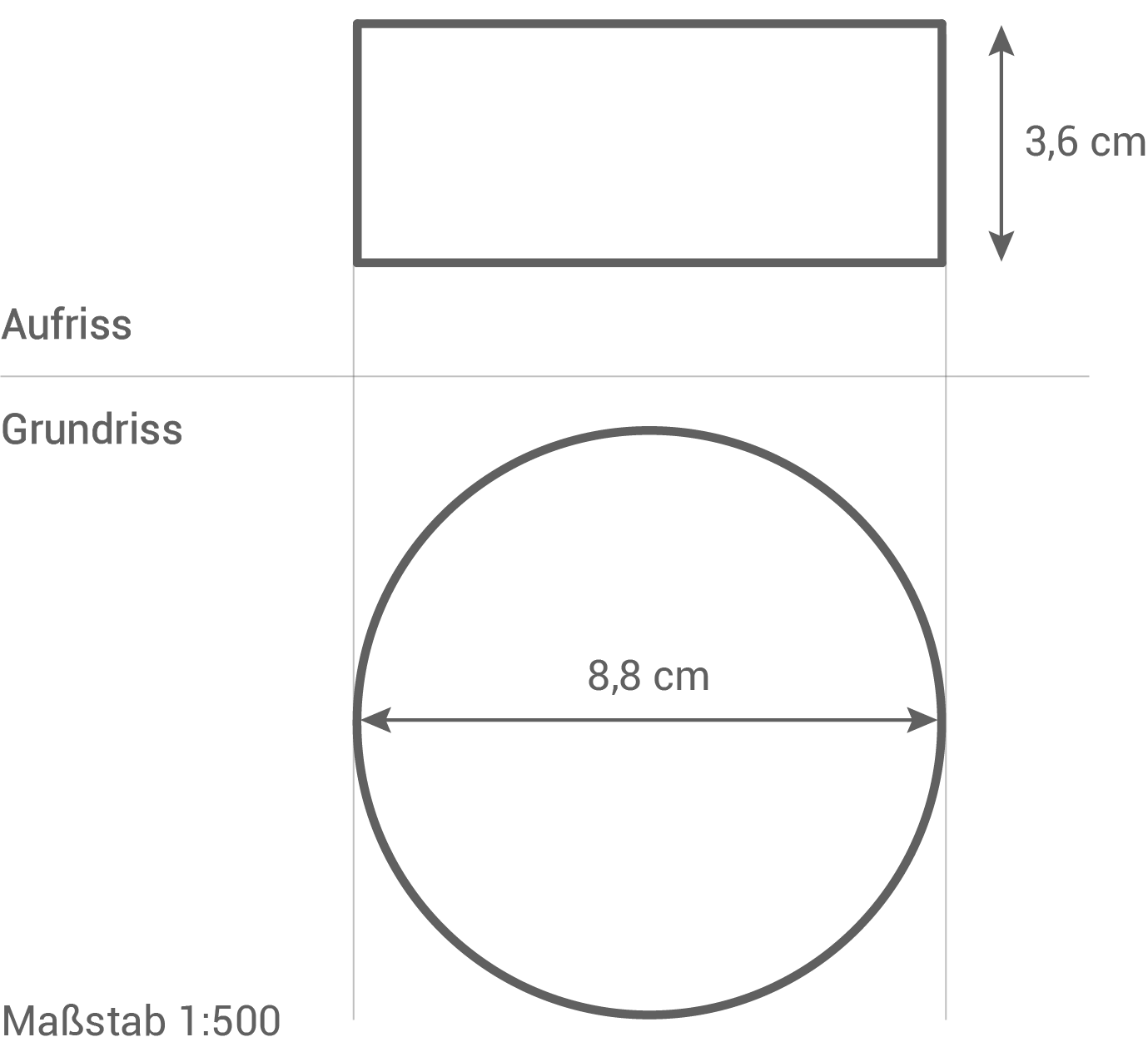
Eines der größten Rundgemälde der Welt ist das Bauernkriegspanorama in Bad Frankenhausen. Es befindet sich in einem zylindrischen und 18 m hohem Ausstellungsgebäude, welches einen Außendurchmesser von 44 m hat.
a)
Stelle das Ausstellungsgebäude im Maßstab 1:500 im Zweitafelbild dar.
(3 BE)
b)
Das Rundgemälde im Inneren des Gebäudes ist 123 m lang und hat einen Flächeninhalt von 
Es kann modellhaft als Mantelfläche eines geraden Kreiszylinders angesehen werden.
Berechne die Höhe und den Durchmesser dieses Kreiszylinders.
Berechne die Höhe und den Durchmesser dieses Kreiszylinders.
(4 BE)
3.
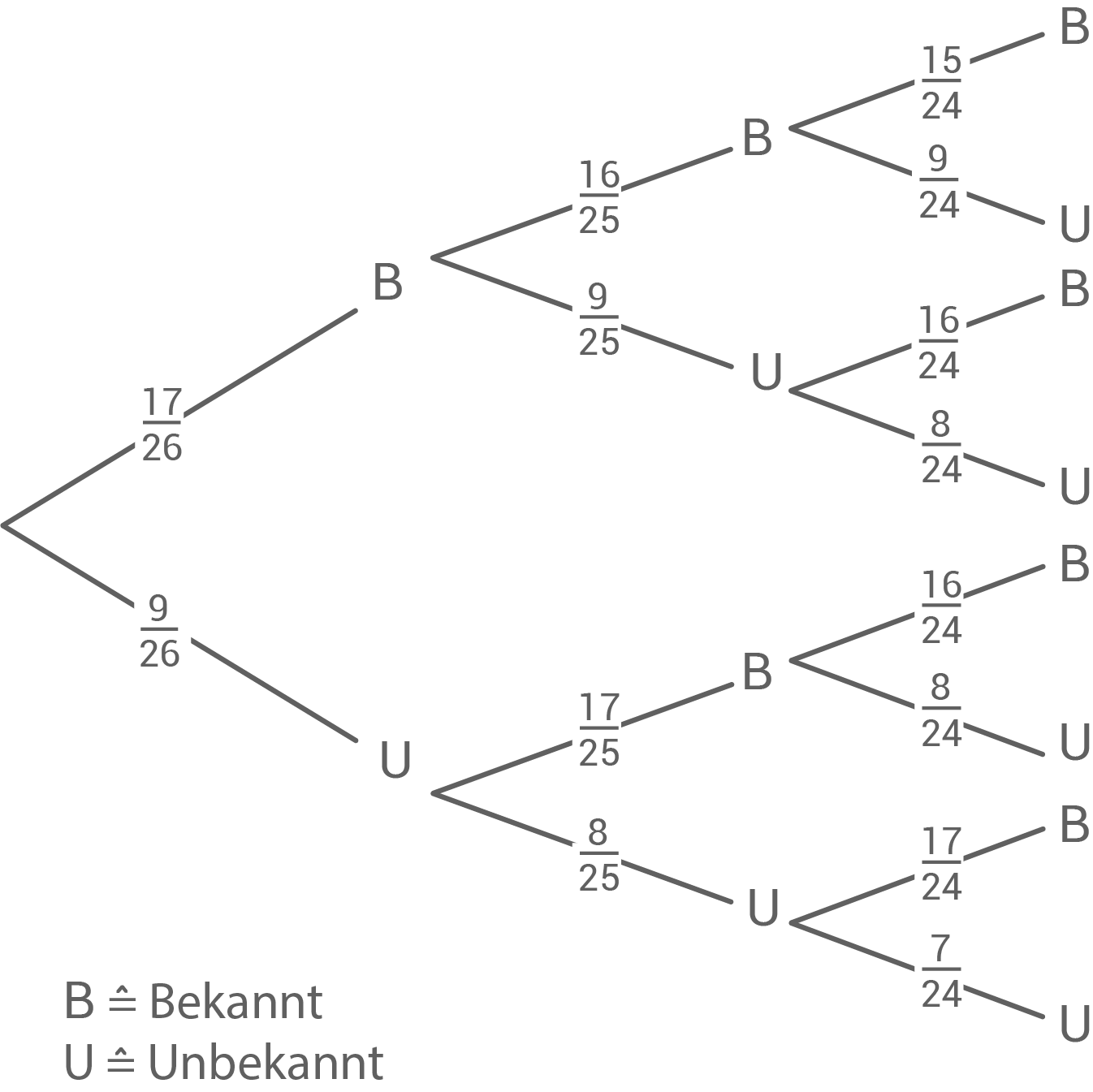
Eine Seminarfachgruppe befragt anonym 26 Jugendliche zur Bekanntheit eines jungen Musikers. Von diesen Jugendlichen gaben 17 an, den Musiker zu kennen. Im Interview wird gefragt, wie die Jugendlichen auf den jungen Musiker aufmerksam geworden sind. Von den 26 Jugendlichen werden drei zufällig interviewt.
Bildnachweise [nach oben]
H.Stolze, Schlachtberg, CC BY-SA 3.0
a)
Berechne die Wahrscheinlichkeit folgender Ereignisse:
A: = „Von drei interviewten Jugendlichen kennt genau einer den jungen Musiker.“
B: = „Höchstens zwei der interviewten Jugendlichen kennen den jungen Musiker nicht.“
(4 BE)
b)
Formuliere ein Ereignis C in Worten zu folgender Gleichung:
(2 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
Punkt 
in 
einsetzen:
![\(\begin{array}[t]{rll}
m\cdot 8+6&=&2 &\quad \scriptsize \mid\;-6 \\[5pt]
8\cdot m&=& -4 &\quad \scriptsize \mid\;:8 \\[5pt]
m&=& -\dfrac{1}{2} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/81c599bb26515544509dfb7aede2d2c89edadfbc264693c92d6f30035a75a580?color=5a5a5a)
b)
Rechteck und Graphen von zeichnen
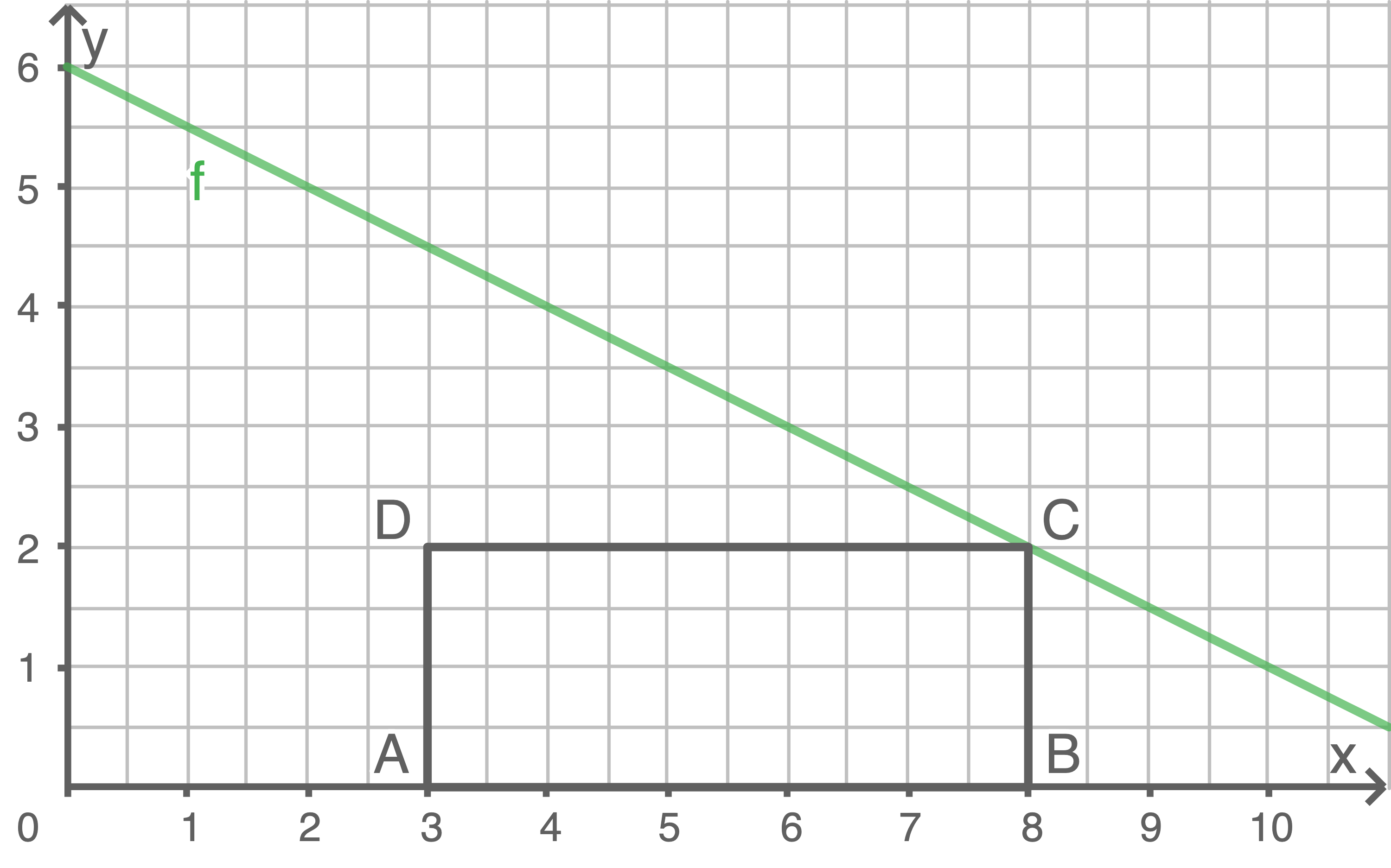Einfluss des Anstiegs auf die Anzahl der Schnittpunkte ermitteln
Der Graph von und das Rechteck haben einen Schnittpunkt, wenn
und das Rechteck haben zwei Schnittpunkte, wenn
und das Rechteck haben keine Schnittpunkte, wenn
(Der Graph von
)
2.
a)
- Außendurchmesser:
- Höhe:
b)
Höhe 
des Kreiszylinders berechnen
![\(\begin{array}[t]{rll}
A_{\text{Rechteck}}&=&a\cdot h & &\quad \scriptsize \mid\; :a\\[5pt]
\dfrac{A_{\text{Rechteck}}}{a}&=& h \\[5pt]
\dfrac{1\,722\,\text{m}^2}{123 \,\text{m}}&=& h \\[5pt]
14\,\text{m}&=& h
\end{array}\)](https://mathjax.schullv.de/6c3439c2a77cfd1db5ca0c78ef4d66bd6324e7c0576490f9ffdbd5c1819d8138?color=5a5a5a)
Durchmesser 
des Kreiszylinders berechnen
![\(\begin{array}[t]{rll}
M_{\text{Kreiszylinder}}&=& 2\pi\cdot r\cdot h &\quad \scriptsize \mid\; :2\pi \,\, \mid\;:h\\[5pt]
\dfrac{M_{\text{Kreiszylinder}}}{2\pi\cdot h}&=& r \\[5pt]
\dfrac{1\,722\,\text{m}^2}{2\pi \cdot 14\,\text{m}}&=& r \\[5pt]
19,6 \,\text{m}&\approx& r
\end{array}\)](https://mathjax.schullv.de/0aeb6e46d48c1677dd72357544666888b620f1b29f5775731f8a687ad3ccdc7f?color=5a5a5a)
Der Durchmesser ist also gegeben durch 
3.
a)
b)
C: = „Höchstens einer von den drei Jugendlichen kennt den Musiker.“