Aufgabe 1
Aufgabenstellung:
In einer Studie zum Spracherwerb von Kindern ist untersucht worden, wie sich die Länge gesprochener Sätze (kurz: Satzlänge) mit dem Alter der Kinder entwickelt.
Ein Sprachforscher modelliert mit einer Funktion die momentane Änderungsrate, mit der sich die durchschnittliche Satzlänge
die momentane Änderungsrate, mit der sich die durchschnittliche Satzlänge der Kinder, die an der Studie teilgenommen haben, im Alter von
der Kinder, die an der Studie teilgenommen haben, im Alter von  Jahren bis
Jahren bis  Jahren verändert. Dazu verwendet er für
Jahren verändert. Dazu verwendet er für  die Gleichung
die Gleichung
 ,
,  .
.
Dabei wird als Maßzahl zur Maßeinheit
als Maßzahl zur Maßeinheit  Jahr und
Jahr und  als Maßzahl zur Maßeinheit
als Maßzahl zur Maßeinheit  Wort pro Jahr aufgefasst.
Wort pro Jahr aufgefasst.
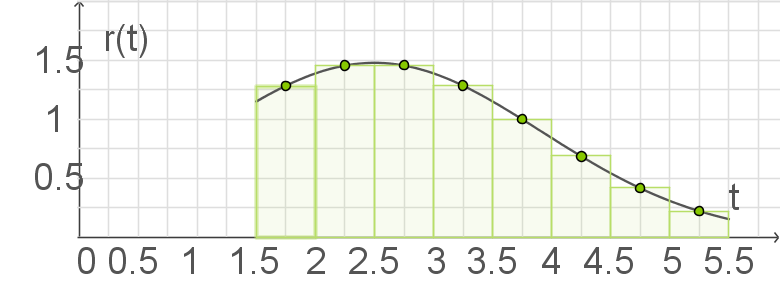
Der Graph von im Bereich
im Bereich  ist in Abbildung 1 dargestellt.
ist in Abbildung 1 dargestellt.
 Im Folgenden wird die durchschnittliche Satzlänge der Kinder, die an der Studie teilgenommen haben, kurz als Satzlänge bezeichnet.
Im Folgenden wird die durchschnittliche Satzlänge der Kinder, die an der Studie teilgenommen haben, kurz als Satzlänge bezeichnet.
Ein Sprachforscher modelliert mit einer Funktion
Dabei wird
Der Graph von
a)
(1)
Berechne den Funktionswert von  an der Stelle
an der Stelle  und interpretiere diesen Wert im Sachzusammenhang.
und interpretiere diesen Wert im Sachzusammenhang.
(2P)
(2)
Für die Funktion  gilt die Aussage:
gilt die Aussage:
 für alle
für alle  .
Interpretiere die Bedeutung dieser Aussage im Sachzusammenhang.
.
Interpretiere die Bedeutung dieser Aussage im Sachzusammenhang.
(3P)
b)
(1)
(2)
Weise rechnerisch nach, dass im gegebenen Modell im Alter von  Jahren die größte momentane Änderungsrate der Satzlänge vorliegt.
Jahren die größte momentane Änderungsrate der Satzlänge vorliegt.
(7P)
(3)
Das Alter zwischen  und
und  Jahren, in dem die momentane Änderungsrate der Satzlänge am schnellsten abnimmt, ist durch die Wendestelle von
Jahren, in dem die momentane Änderungsrate der Satzlänge am schnellsten abnimmt, ist durch die Wendestelle von  im Intervall [
im Intervall [ ] gegeben.
] gegeben.
Ermittle diese Wendestelle.
[Hinweis: Auf den Nachweis einer hinreichenden Bedingung kann verzichtet werden.]
Ermittle diese Wendestelle.
[Hinweis: Auf den Nachweis einer hinreichenden Bedingung kann verzichtet werden.]
(5P)
c)
In der Studie ist bei den Kindern im Alter von  Jahren eine Satzlänge von
Jahren eine Satzlänge von  Wörtern beobachtet worden.
Wörtern beobachtet worden.
 mit Hilfe eines Integrationsverfahrens ist nicht möglich. Daher wird der Wert des Integrals
mit Hilfe eines Integrationsverfahrens ist nicht möglich. Daher wird der Wert des Integrals  durch ein numerisches Verfahren bestimmt. In Abbildung 2 ist dieses Verfahren veranschaulicht.
durch ein numerisches Verfahren bestimmt. In Abbildung 2 ist dieses Verfahren veranschaulicht.
(1)
Interpretiere die Bedeutung der Terme  und
und  im Sachzusammenhang.
im Sachzusammenhang.
Die konkrete Ermittlung eines Funktionsterms einer Stammfunktion von
(4P)
(2)
Beschreibe kurz das Vorgehen bei diesem numerischen Verfahren.
(4P)
(3)
Berechne mit diesem numerischen Verfahren einen Nährungswert für den Term  .
.
(6P)
d)
Für  ist die Funktion
ist die Funktion  definiert durch die Gleichung
definiert durch die Gleichung  .
.
Bildnachweise [nach oben]
(1)
Interpretiere, welche Bedeutung die Funktion  im Sachzusammenhang hat.
im Sachzusammenhang hat.
(2P)
(2)
Begründe, warum für die Ableitung der Funktion  mit
mit  gilt:
gilt:
 .
[Du kannst davon ausgehen, dass es eine Stammfunktion
.
[Du kannst davon ausgehen, dass es eine Stammfunktion  von
von  gibt. Wie bereits in c) angegeben, ist die konkrete Ermittlung eines Funktionsterms von
gibt. Wie bereits in c) angegeben, ist die konkrete Ermittlung eines Funktionsterms von  mit Hilfe eines Integrationsverfahrens aber nicht möglich.]
mit Hilfe eines Integrationsverfahrens aber nicht möglich.]
Für die Funktion wird folgende Berechnung durchgeführt, die von dir in den Teilaufgaben (3) und (4) zum Teil nachvollzogen und interpretiert werden soll:
II
wird folgende Berechnung durchgeführt, die von dir in den Teilaufgaben (3) und (4) zum Teil nachvollzogen und interpretiert werden soll:
II  .
.
Für die Funktion
(3P)
(3)
Weise nach, dass gilt:  (siehe I).
(siehe I).
(3P)
(4)
Interpretiere die Lösung  der Gleichung
der Gleichung  (siehe I ) unter Berücksichtigung von II im Sachzusammenhang.
(siehe I ) unter Berücksichtigung von II im Sachzusammenhang.
(3P)
© 2016 - SchulLV.
© 2016 - SchulLV.
a)
(1)
(2)
b)
(1)
(2)
- Notwendige Bedingung:
- Hinreichende Bedingung:
- Prüfe die notwendige Bedingung
- Prüfe die hinreichende Bedingung
(3)
- Notwendige Bedingung:
- Hinreichende Bedingung:
Nach dem Satz vom Nullprodukt kann nur der Klammerterm der zweiten Ableitung gleich Null werden. Untersuche daher den Term  mit deinem GTR auf Nullstellen.
Lasse dir den Graphen zeichnen und bestimme mit folgendem Befehl die Nullstelle.
mit deinem GTR auf Nullstellen.
Lasse dir den Graphen zeichnen und bestimme mit folgendem Befehl die Nullstelle.
 Wähle als Grenzen die Grenzen des Intervalls
Wähle als Grenzen die Grenzen des Intervalls ![\( [1,5;5,5]\)](https://www.schullv.de/resources/formulas/caf3947d92c8bdd1f746d401bece571e2e7b31b903534c13bbbef2cb2afda554_light.svg) . Du erhältst eine Nullstelle an der Stelle
. Du erhältst eine Nullstelle an der Stelle  .
.
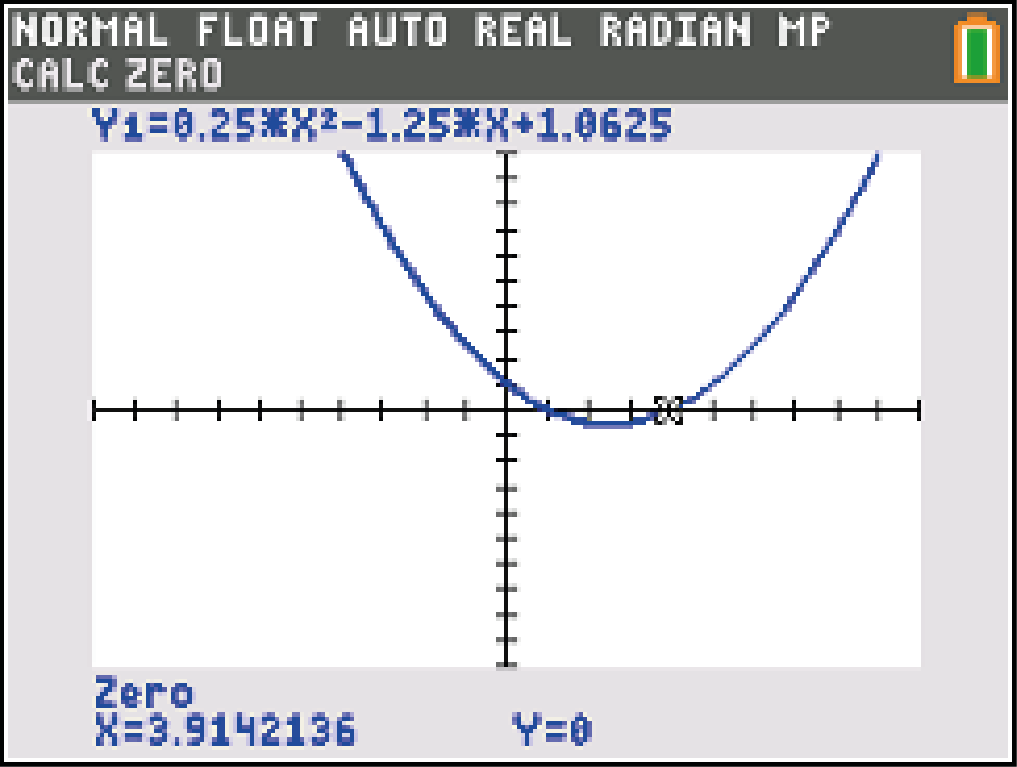 Abb. 1: Berechnung der Wendestelle.
Abb. 1: Berechnung der Wendestelle.
c)
(1)
(2)
(3)
d)
(1)
(2)
(3)
(4)
© 2016 - SchulLV.
a)
(1)
(2)
b)
(1)
(2)
- Notwendige Bedingung:
- Hinreichende Bedingung:
- Prüfe die notwendige Bedingung
- Prüfe die hinreichende Bedingung
(3)
- Notwendige Bedingung:
- Hinreichende Bedingung:
Nach dem Satz vom Nullprodukt kann nur der Klammerterm der zweiten Ableitung gleich Null werden. Untersuche daher den Term  mit deinem GTR auf Nullstellen.
Lasse dir den Graphen zeichnen und bestimme mit folgendem Befehl die Nullstelle.
mit deinem GTR auf Nullstellen.
Lasse dir den Graphen zeichnen und bestimme mit folgendem Befehl die Nullstelle.

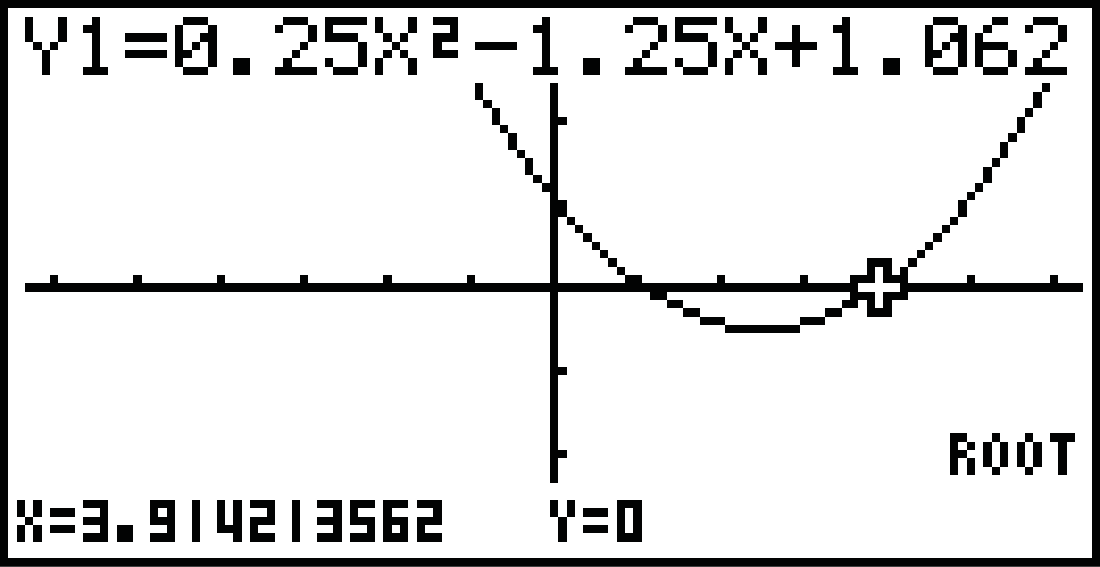 Abb. 1: Berechnung der Wendestelle.
Abb. 1: Berechnung der Wendestelle.
c)
(1)
(2)
(3)
d)
(1)
(2)
(3)
(4)
© 2016 - SchulLV.