Teil B

Gegeben ist die Schar der in $\mathbb{R}$ definierten Funktionen $f_b: x \mapsto \dfrac{1}{16}x^2 \cdot \mathrm{e}^{-b \cdot x+4 b}$ mit $b \in \mathbb{R}^{+}.$ Der Graph von $f_{b}$ wird mit $G_{b}$ bezeichnet.

Gib das Verhalten von $f_b$ für $x \rightarrow-\infty$ und für $x \rightarrow+\infty$ an.

Zeige, dass der Funktionswert von $f_b$ an der Stelle $4$ unabhängig von $b$ ist.

(3 BE)

Bestimme rechnerisch die Koordinaten und die Art der beiden Extrempunkte von $G_b.$ Berechne einen Wert von $b,$ für den die beiden Extrempunkte den Abstand $6$ haben, und gib diesen Wert auf zwei Nachkommastellen gerundet an.

(6 BE)

Begründe, ohne Terme von Stammfunktionen zu bestimmen, dass die folgende Aussage wahr ist:

Der Graph jeder Stammfunktion von $f_b$ hat mit der positiven $x$ -Achse höchstens einen gemeinsamen Punkt.

(3 BE)

Betrachtet wird nun die in $\mathbb{R}$ definierte Funktion $r: x \mapsto \dfrac{1}{16} x^2 \cdot \mathrm{e}^{-0,25 x+1}.$

Somit ist $r$ die Funktion $f_{0,25}$ der Schar aus Aufgabe 1. Ihr Graph wird mit $G$ bezeichnet.

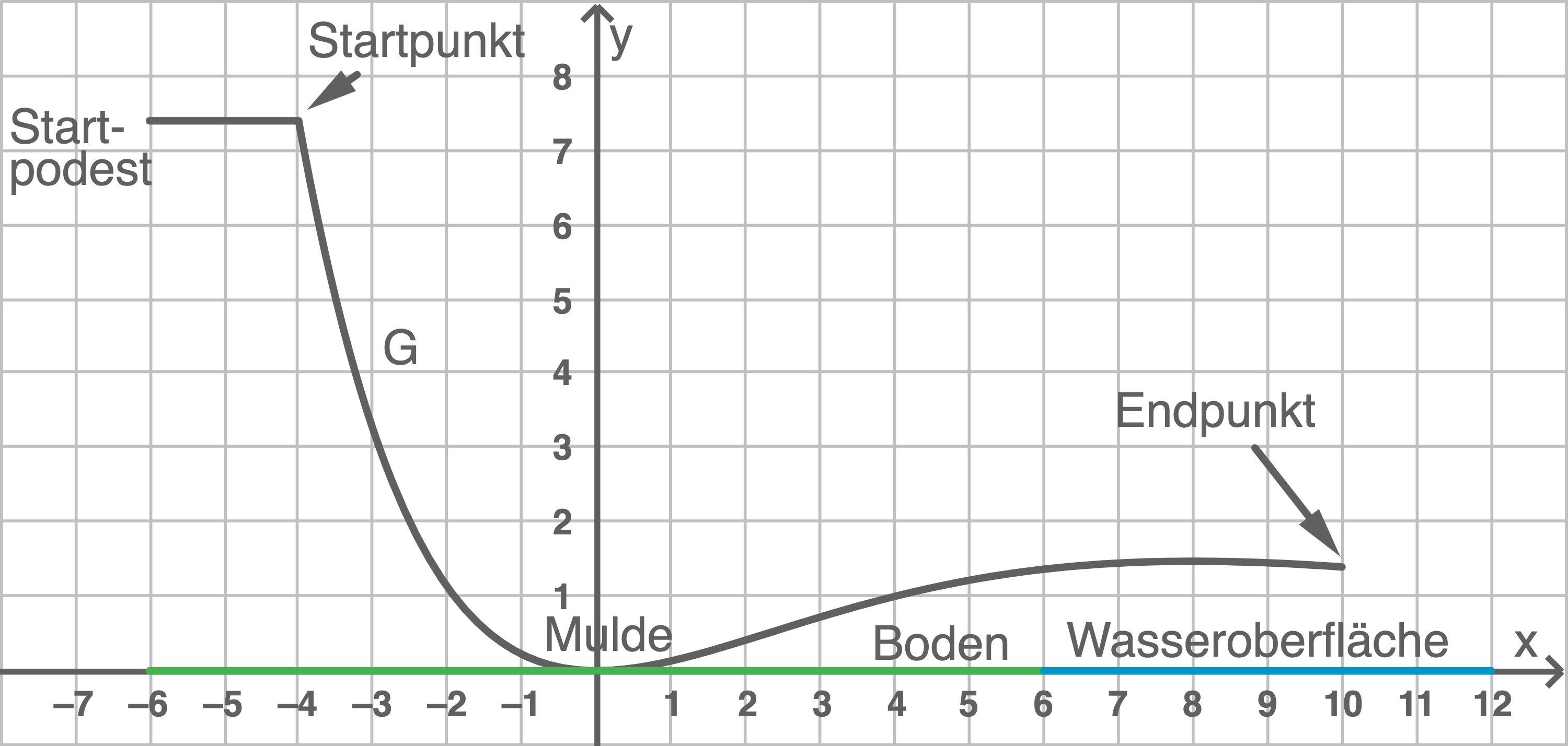
Diagramm mit einem Graphen, der den Verlauf von Höhenpunkten und Wasseroberfläche zeigt.

Abb. 1

Die Konstruktion einer Wasserrutsche, die aus einer Rutschbahn und einem horizontalen Startpodest besteht, wird geplant. Dabei beschreibt $G$ für $-4 \leq x \leq 10$ die Profillinie der Rutschbahn und die $x$ -Achse den horizontalen Boden sowie die Wasseroberfläche (vgl. Abbildung 1). Eine Längeneinheit im Koordinatensystem entspricht dabei $1\;\text{m}$ in der Realität.

Berechne die Höhe des Startpodests über dem Boden und die Höhe des Endpunkts der Rutschbahn über der Wasseroberfläche.

(3 BE)

Betrachtet wird der Winkel $\beta,$ der im Sachzusammenhang von Bedeutung ist. Mithilfe der folgenden beiden Gleichungen kann $\beta$ ermittelt werden:

$\(r$

$\beta=180^\circ-\left| \alpha \right|$

Zeichne die Winkel $\alpha$ und $\beta$ in Abbildung 1 geeignet ein und gib die Bedeutung von $\beta$ im Sachzusammenhang an.

(4 BE)

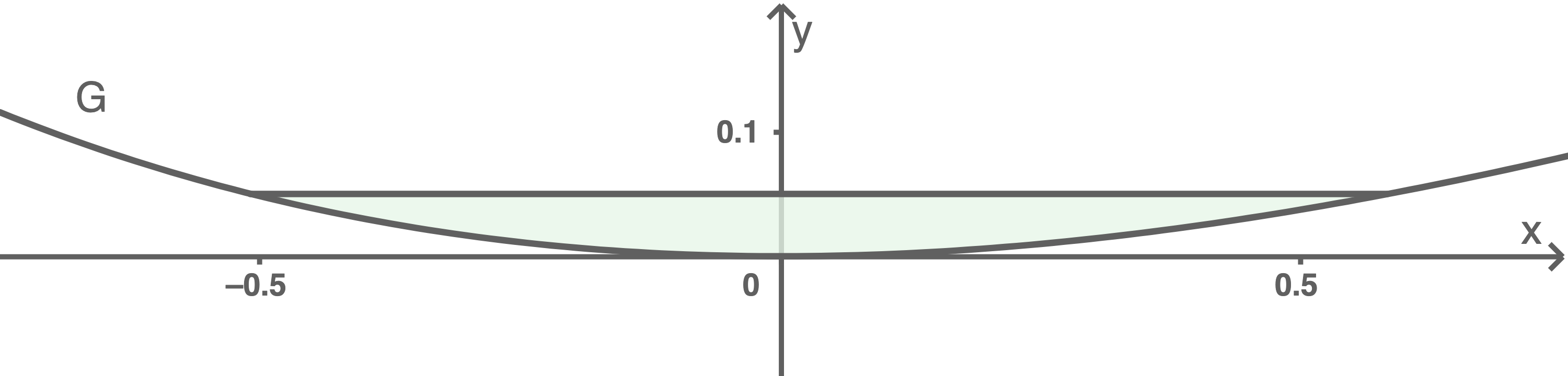
Da die $1,5 \;\text{m}$ breite Rutschbahn durch vertikale Wände begrenzt werden soll, kann sich Wasser in der Mulde sammeln. Berechne das Volumen des Wassers in der Mulde in Litern, wenn es dort an der tiefsten Stelle eine Höhe von $5\;\text{cm}$ hat (vgl. Abbildung 2).

Grafik eines mathematischen Graphen mit Achsenbeschriftungen und einer schattierten Fläche.

Abb. 2

(6 BE)

In der folgenden Untersuchung wird erneut nur die Profillinie der Rutschbahn betrachtet. Um die Sicherheit der Badegäste zu erhöhen, soll eine in alle Richtungen drehbare Überwachungskamera angebracht werden, deren Position im Modell durch den Punkt $(12\mid3)$ beschrieben wird. Die Sichtlinie der Kamera in Richtung eines Punkts der Rutschbahn, der durch $(a \mid r(a))$ mit $-4 \leq a \leq 10$ dargestellt wird, kann durch die Gerade $g_a$ mit der Gleichung $y=\frac{3-r(a)}{12-a} \cdot x+\left(3-\frac{3-r(a)}{12-a} \cdot 12\right)$ beschrieben werden.

Untersuche rechnerisch, ob der Teil der Rutschbahn, der durch den rechtsgekrümmten Teil von $G$ dargestellt wird, von der Kamera vollständig einsehbar ist.

(5 BE)

(30 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Grenzwertverhalten angeben

$\begin{array}[t]{rlll} \lim\limits_{x\to-\infty}f_b(x)&=&+\infty \\[5pt] \lim\limits_{x\to+\infty}f_b(x)&=&0 \end{array}$

Unabhängigkeit des Funktionswerts zeigen

$\begin{array}[t]{rlll} f_b(4)&=&\dfrac{1}{16}\cdot4^2 \cdot \mathrm{e}^{-b \cdot 4+4 b} \\[5pt] &=&1 \cdot \mathrm{e}^{0} \\[5pt] &=&1 \end{array}$

Für die erste Ableitung von $f_b$ folgt mit dem CAS:

$\(f_b$

Anwenden der notwendingen Bedingung $\(f_b$ und auflösen nach $x$ mit dem CAS liefert:

$\begin{array}[t]{rlll} x_1&=&0 \\[5pt] x_2&=&\dfrac{2}{b} \end{array}$

Auf das Überprüfen der hinreichenden Bedingung kann verzichtet werden, da die Aufgabenstellung besagt, dass $G_b$ genau zwei Extrempunkte besitzt. Einsetzen in $f_b(x)$ liefert:

$\begin{array}[t]{rlll} f_b(0)&=&\dfrac{1}{16}\cdot0^2\cdot\mathrm e^{-b\cdot0+4b} \\[5pt] &=&0\cdot\mathrm e^{4b} \\[5pt] &=&0 \end{array}$

$\begin{array}[t]{rlll} f_b\left(\dfrac{2}{b}\right)&=&\dfrac{1}{16}\cdot\left(\dfrac{2}{b}\right)^2\cdot\mathrm e^{-b\cdot\frac{2}{b}+4b} \\[5pt] &=&\dfrac{1}{4b^2}\cdot\mathrm e^{-2+4b} \end{array}$

Da $\frac{1}{4b^2}\cdot\mathrm e^{-2+4b}\gt0$ gilt, besitzt $G_b$ bei $x_1=0$ einen Tiefpunkt, und bei $x_2=\frac{2}{b}$ einen Hochpunkt. Für die gesuchten Koordinaten gilt also $T(0\mid0)$ und $H(\frac{2}{b}\mid\frac{1}{4b^2}\cdot\mathrm e^{-2+4b}).$
Der gesuchte Wert von $b$ ergibt sich aus folgender Gleichung:

$\sqrt{(\frac{2}{b}-0)^2+(\frac{1}{4b^2}\cdot\mathrm e^{-2+4b}-0)^2}=6$

Auflösen nach $b$ mit dem solve-Befehl des CAS liefert:

$\begin{array}[t]{rlll} b_1&\approx&-0,33 \\[5pt] b_2&\approx&0,34 \end{array}$

Da $b\gt0$ gilt, ist $b_2\approx0,34$ der gesuchte Wert.

Für jeden Wert von $b$ besitzt $f_b$ nur eine Nullstelle, die bei $x=0$ liegt. Somit besitzt jede Stammfunktion von $f_b$ höchstens eine Maximalstelle, die bei $x=0$ liegt. Somit ändert sich das Monotonieverhalten aller Stammfunktion von $f_b$ für positive $x$ -Werte nicht, sodass der Graph jeder dieser Stammfunktionen von $f_b$ mit der positiven $x$ -Achse höchstens einen gemeinsamen Punkt besitzt.

$\begin{array}[t]{rlll} r(-4)&=&\dfrac{1}{16}\cdot(-4)^2\cdot\mathrm e^{-0,25\cdot(-4)+1} \\[5pt] &=&\mathrm e^2 \\[5pt] &\approx&7,39 \end{array}$

$\begin{array}[t]{rlll} r(10)&=&\dfrac{1}{16}\cdot10^2\cdot\mathrm e^{-0,25\cdot10+1} \\[5pt] &\approx&1,4 \end{array}$

Das Startpodest befindet sich somit ca. $7,39\;\text{m}$ über dem Boden und das Ende der Rutschbahn ca. $1,4\;\text{m}$ über der Wasseroberfläche.

Winkel geeignet einzeichnen

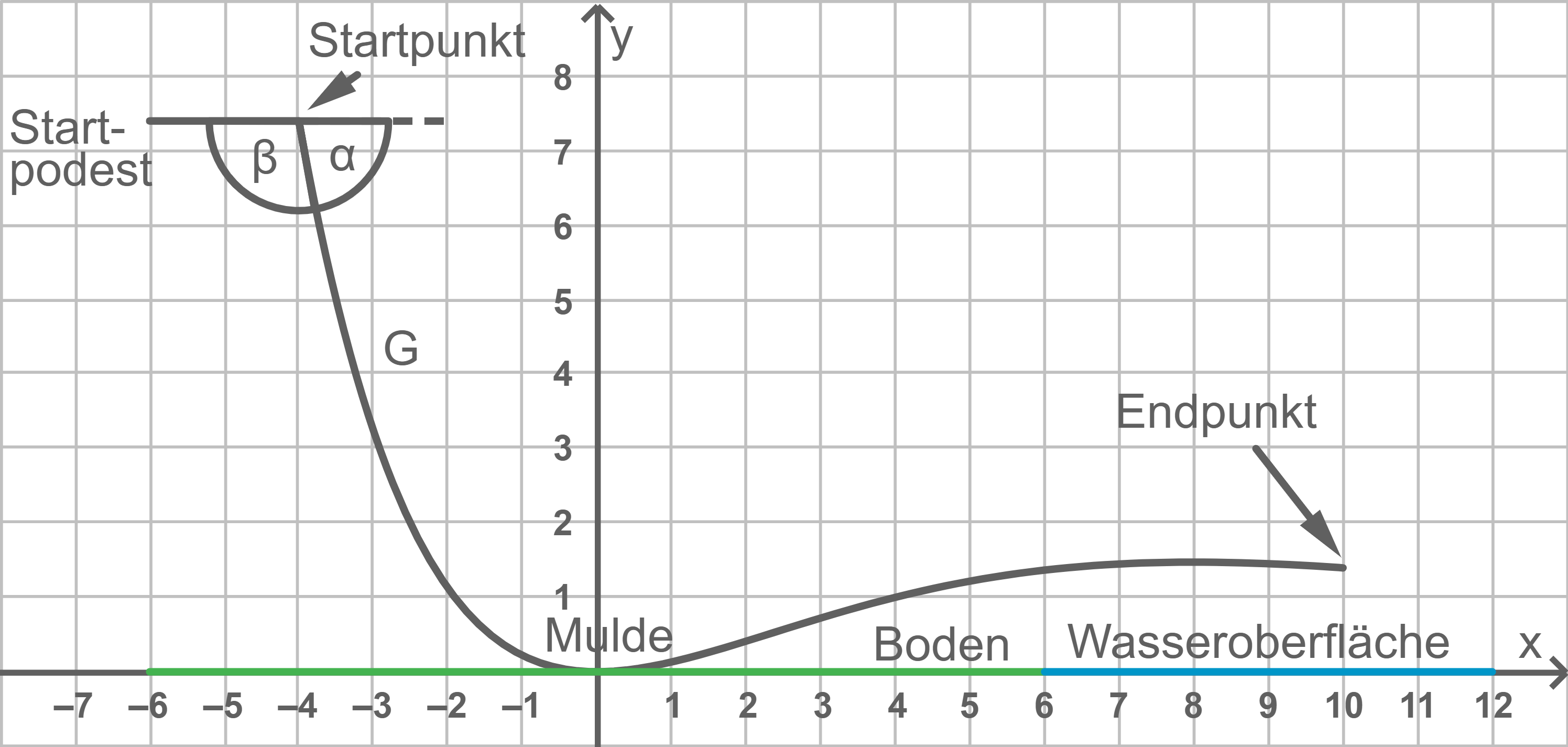
Diagramm mit einem Startpodest, einer Mulde und einem Endpunkt, das eine Bewegungskurve zeigt.

Bedeutung von $\boldsymbol{\beta}$ im Sachzusammenhang angeben

Der Winkel $\beta$ beschreibt den Winkel, den die Wasserrutsche mit dem Startpodest einschließt.

Auflösen der Gleichung $r(x)=0,05$ nach $x$ mit dem solve-Befehl des CAS liefert:

$\begin{array}[t]{rlll} x_1&\approx&-0,51 \\[5pt] x_2&\approx&0,58 \end{array}$

Der folgende Term beschreibt somit das Volumen des Wassers:

$1,5\cdot\displaystyle\int_{-0,51}^{0,58}(0,05-f(x))\;\mathrm dx$

Berechnen des Integrals mit dem CAS ergibt:

$1,5\cdot\displaystyle\int_{-0,51}^{0,58}(0,05-f(x))\;\mathrm dx\approx0,05448\;\text{m}^3$

Umrechnen dieses Ergebnisses in Liter liefert, dass das Wasser in der Mulde ein Volumen von $0,05448\cdot1000=54,48\;\ell$ hat.

Für die zweite Ableitung von $r$ folgt mit dem CAS:

$\(r$

Nullsetzen liefert mit dem CAS:

$\begin{array}[t]{rlll} x_1&\approx&2,34 \\[5pt] x_2&\approx&13,66 \end{array}$

Mit Hilfe der graphischen Funktion des CAS lässt sich erkennen, dass $r$ bei $x_1$ eine Wendestelle besitzt, ab der $G$ bis zum Ende der Wasserrutsche rechtsgekrümmt ist. Da $x_1$ eine links-rechts Wendestelle ist, besitzt $r$ an diesem Punkt zudem die größte Steigung.Falls die Gerade $g_a$ für $a=x_1$ keinen weiteren Punkt von $r$ enthält, kann die Kamera somit den gesamten rechtgekrümmten Bereich der Rutsche einsehen.
Einsetzen von $y=r(x)$ und $a=x_1$ in die Gleichung der Geraden $g_a$ liefert:

$\dfrac{1}{16} x^2 \cdot \mathrm{e}^{-0,25 x+1}=\dfrac{3-\frac{1}{16}\cdot (2,34)^2 \cdot \mathrm{e}^{-0,25\cdot2,34+1}}{12-2,34} \cdot x+\left(3-\dfrac{3-\frac{1}{16}\cdot(2,34)^2 \cdot \mathrm{e}^{-0,25\cdot2,34+1}}{12-2,34} \cdot 12\right)$

Auflösen nach $x$ mit dem solve-Befehl des CAS liefert:

$\begin{array}[t]{rlll} x_1&\approx&2,34 \\[5pt] x_2&\approx&5,19 \end{array}$

Da $x_2$ auf dem rechtsgekrümmten Teil der Wasserrutsche liegt und nicht $x_1$ entspricht, besitzt die direkte Verbindung des links-rechts Wendepunkts von $r$ zur Kamera einen Schnittpunkt mit der Funktion $r,$ sodass die Kamera nicht den gesamten Teil der Wasserrutsche einsehen kann, der durch den rechtsgekrümmt Abschnitt von $G$ beschrieben wird.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?