Mathe Abi 2025 Bayern Gymnasium G8/G9 Analysis Aufg. 1A

1

Gegeben ist die in $\mathbb{R} \setminus\{0\}$ definierte Funktion $f: x \mapsto \dfrac{1}{x^2}+1.$

a)

Gib eine Gleichung der senkrechten und eine Gleichung der waagerechten Asymptote des Graphen von $f$ an.

(2 BE)

b)

Berechne den Wert des Integrals $\displaystyle\int_1^2 f(x) \;\text{d} x.$

(3 BE)

2

Gegeben ist die in $\mathbb{R}$ definierte Funktion $g: x \mapsto x^2-\mathrm{e}^{x}.$ Der Graph von $g$ besitzt genau einen Wendepunkt $W.$ Bestimme rechnerisch die $x$ -Koordinate von $W$ und beurteile, ob $W$ oberhalb der $x$ -Achse liegt.

(5 BE)

3

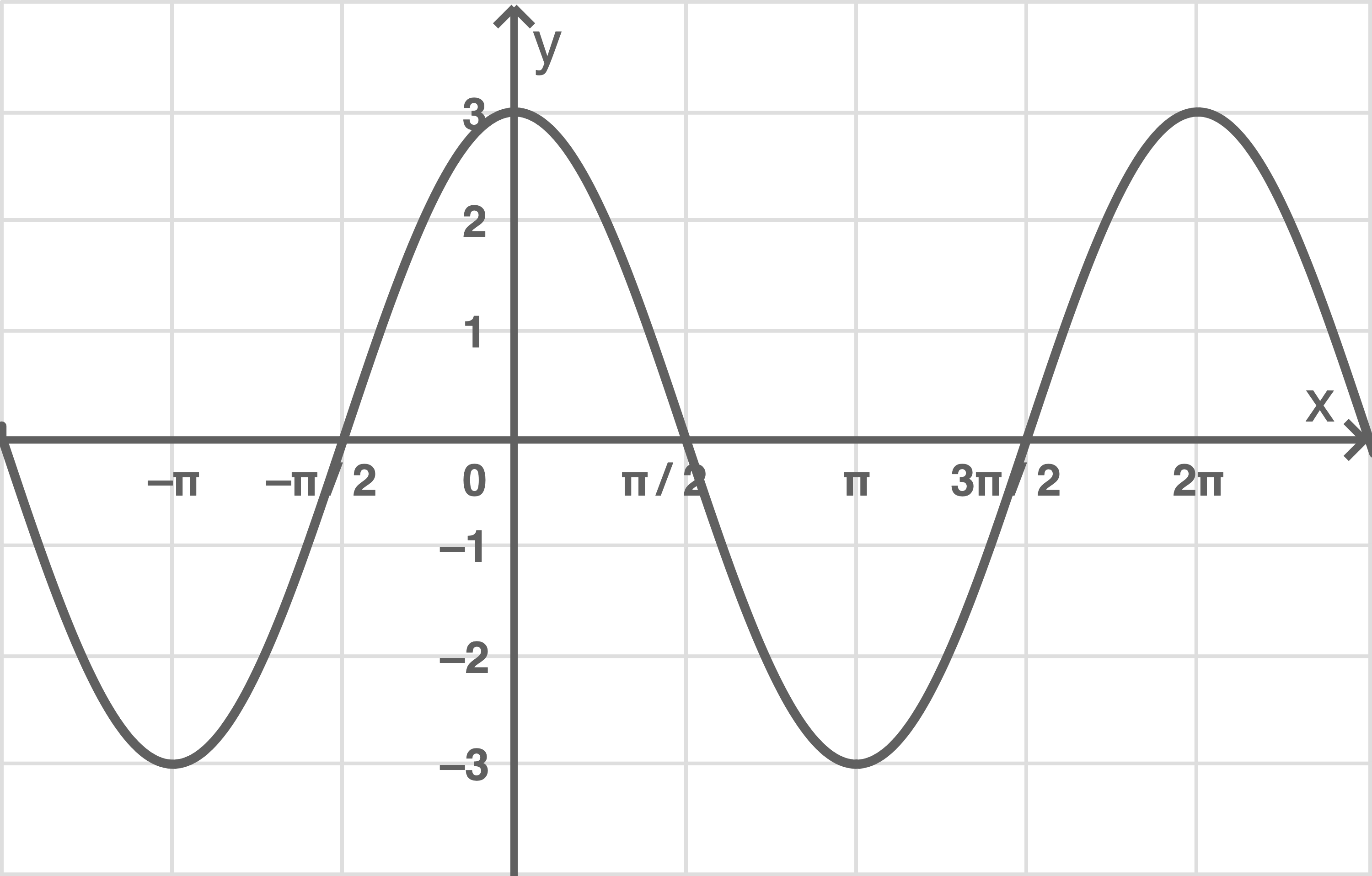
Abbildung 1 zeigt den Graphen der in $\mathbb{R}$ definierten Funktion $f$ mit $f(x)=3 \cdot \cos (x).$

a)

Gib den Wert des Integrals $\displaystyle\int_{0}^{\pi}f(x)\;\mathrm{d}x$ an.

(1 BE)

b)

Die in $\mathbb{R}$ definierte Funktion $g$ ist gegeben durch $g(x)=a \cdot f(x)+b \cdot x$ mit reellen Zahlen $a$ und $b$ . Die Punkte $(0 \mid-3)$ und $\left(\frac{\pi}{2} \mid \frac{3}{4} \pi\right)$ liegen auf dem Graphen von $g.$

Ermittle $a$ und $b.$

(4 BE)

Graph einer Sinusfunktion mit Achsenbeschriftungen für x und y.

Abb. 1

4

Gegeben sind die in $\mathbb{R}_0^{+}$ definierten Funktionen $f$ und $g,$ wobei $g$ die Umkehrfunktion von $f$ ist. Abbildung 2 zeigt die Graphen $G_f$ von $f$ und $G_g$ von $g.$ $G_f$ und $G_g$ schneiden sich nur im Koordinatenursprung und im Punkt $(x_S \mid f(x_S)).$ Beurteile die folgende Aussage:

$\displaystyle\int_{0}^{x_S}(g(x)-f(x))\;\mathrm{d}x= 2\cdot \displaystyle\int_{0}^{x_S}(x-f(x))\;\mathrm{d}x$

Abb. 2

(5 BE)

(20 BE)

Teil A

Weiter lernen mit SchulLV-PLUS!

Weiter lernen mit SchulLV-PLUS!