Teil B

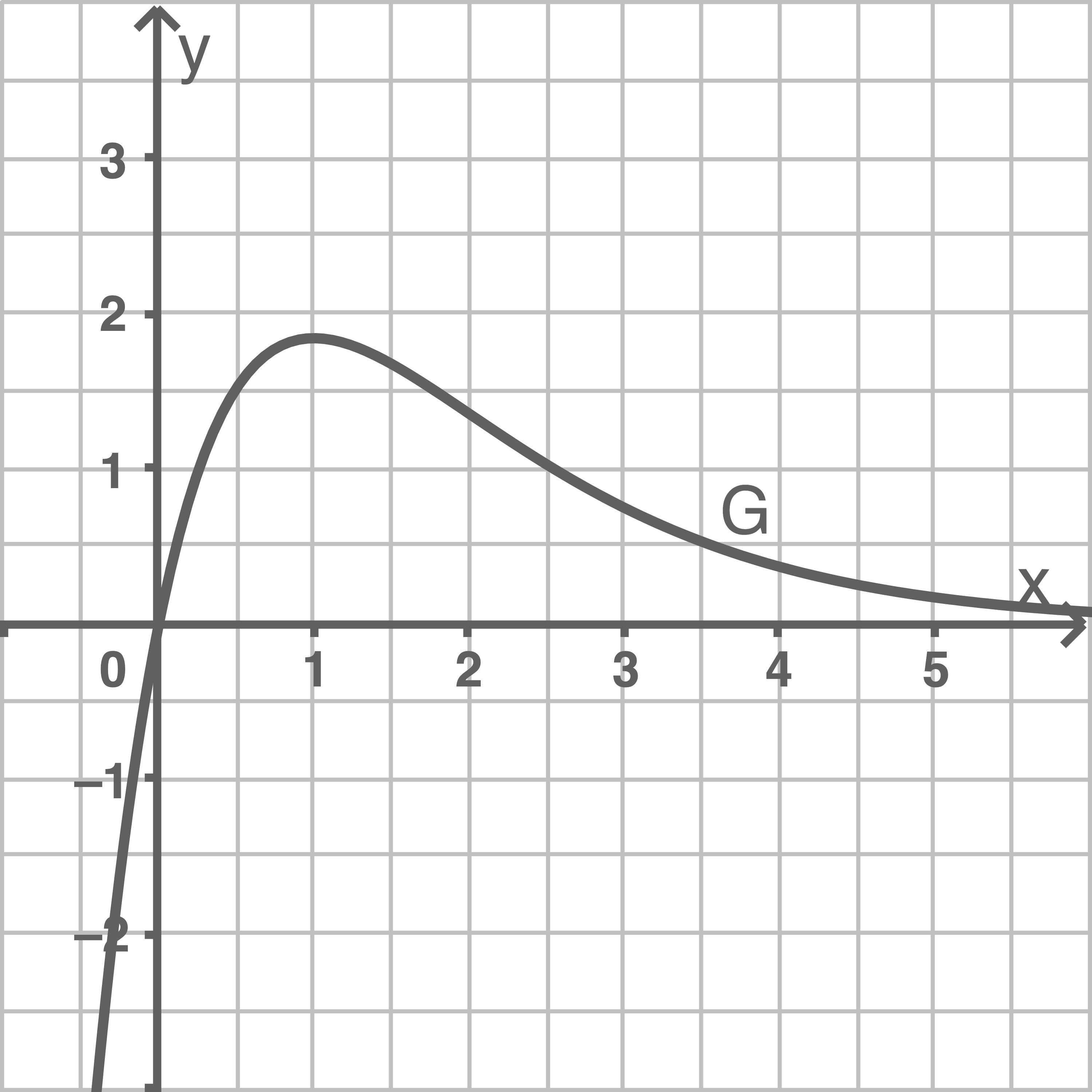
Gegeben ist die in $\mathbb{R}$ definierte Funktion $f: x \mapsto 5 x \cdot \mathrm{e}^{-x}.$ Abbildung 1 zeigt den Graphen $G$ von $f.$

$G$ hat genau einen Extrempunkt. Berechne die Koordinaten des Extrempunkts von $G.$

$\left(\text{zur Kontrolle:} \left(1 \,\bigg\vert\, \dfrac{5}{\text{e}}\right)\right)$

(4 BE)

Die Tangente $t$ an $G$ in dessen Wendepunkt hat die Gleichung $y=-\frac{5}{\mathrm{\text{e}}^2}x+\frac{20}{\mathrm{e}^2}.$ Ermittle eine Gleichung der Gerade, die den Extrempunkt von $G$ enthält und senkrecht zu $t$ verläuft.

(3 BE)

Graf einer Funktion im Koordinatensystem mit Achsenbeschriftung und Verlauf der Kurve.

Abb. 1

Betrachtet wird die in $[1 ;+\infty[$ definierte Funktion $h$ mit $h(x)=f(x).$

Begründe, dass die Funktion $f$ nicht umkehrbar, die Funktion $h$ jedoch umkehrbar ist. Gib den Definitions- und den Wertebereich der Umkehrfunktion von $h$ an.

(6 BE)

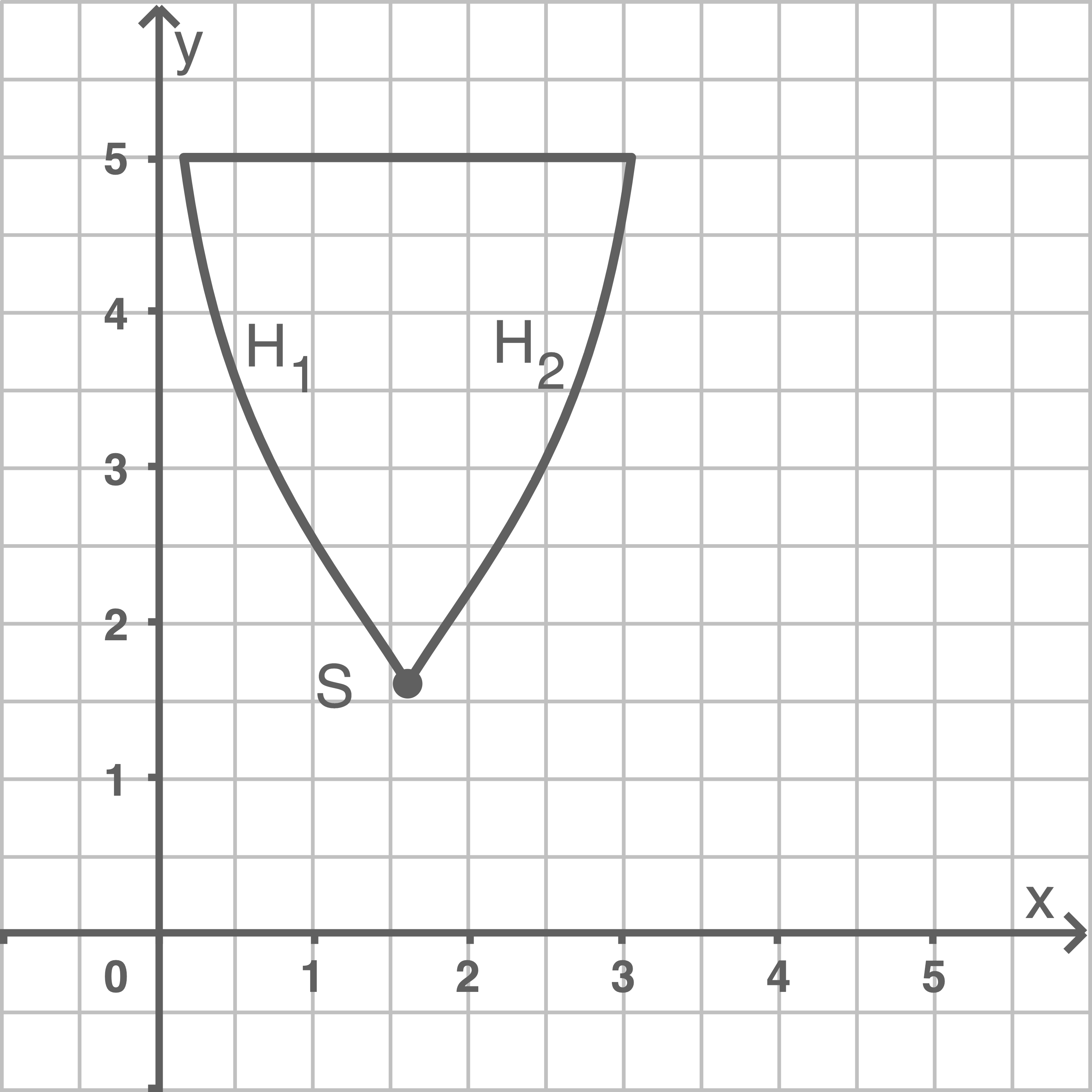
Abbildung 2 zeigt eine Figur, die modellhaft das Wappen eines Sportvereins beschreibt. Die Begrenzungslinien der Figur werden durch einen Teil der Gerade mit der Gleichung $y = 5$ sowie durch die Kurvenstücke $H_1$ und $H_2$ beschrieben:

$H_1$ entsteht, indem $G$ für $x \in[\ln 5 ; 5]$ an der Gerade mit der Gleichung $y=x$ gespiegelt wird.
$H_2$ entsteht durch Spiegeln von $H_1$ an der Gerade mit der Gleichung $x=\ln 5.$

Der Punkt $S(\ln 5 \mid \ln 5)$ ist gemeinsamer Punkt von $H_1$ und $H_2.$

Graph einer Parabel mit den Punkten H1, H2 und S im Koordinatensystem.

Abb. 2

Begründe, dass mit dem Term $2 \cdot\left((5-\ln 5) \cdot \ln 5-\displaystyle\int_{\ln 5}^5 f(x) \;\mathrm{d} x\right)$ der Flächeninhalt der Figur berechnet werden kann.

(5 BE)

Die in $\mathbb{R}$ definierte Funktion $F: x \mapsto-5(x+1) \cdot \mathrm{e}^{-x}$ ist eine Stammfunktion von $f.$ Berechne mit dem Term aus Aufgabe 1d den Flächeninhalt der Figur auf eine Nachkommastelle genau.

(3 BE)

Betrachtet wird die Schar der in $\mathbb{R}$ definierten Funktionen $g_k: x \mapsto-5 x \cdot \mathrm{e}^{-kx}$ mit $k \in \mathbb{R} \backslash\{0\}.$
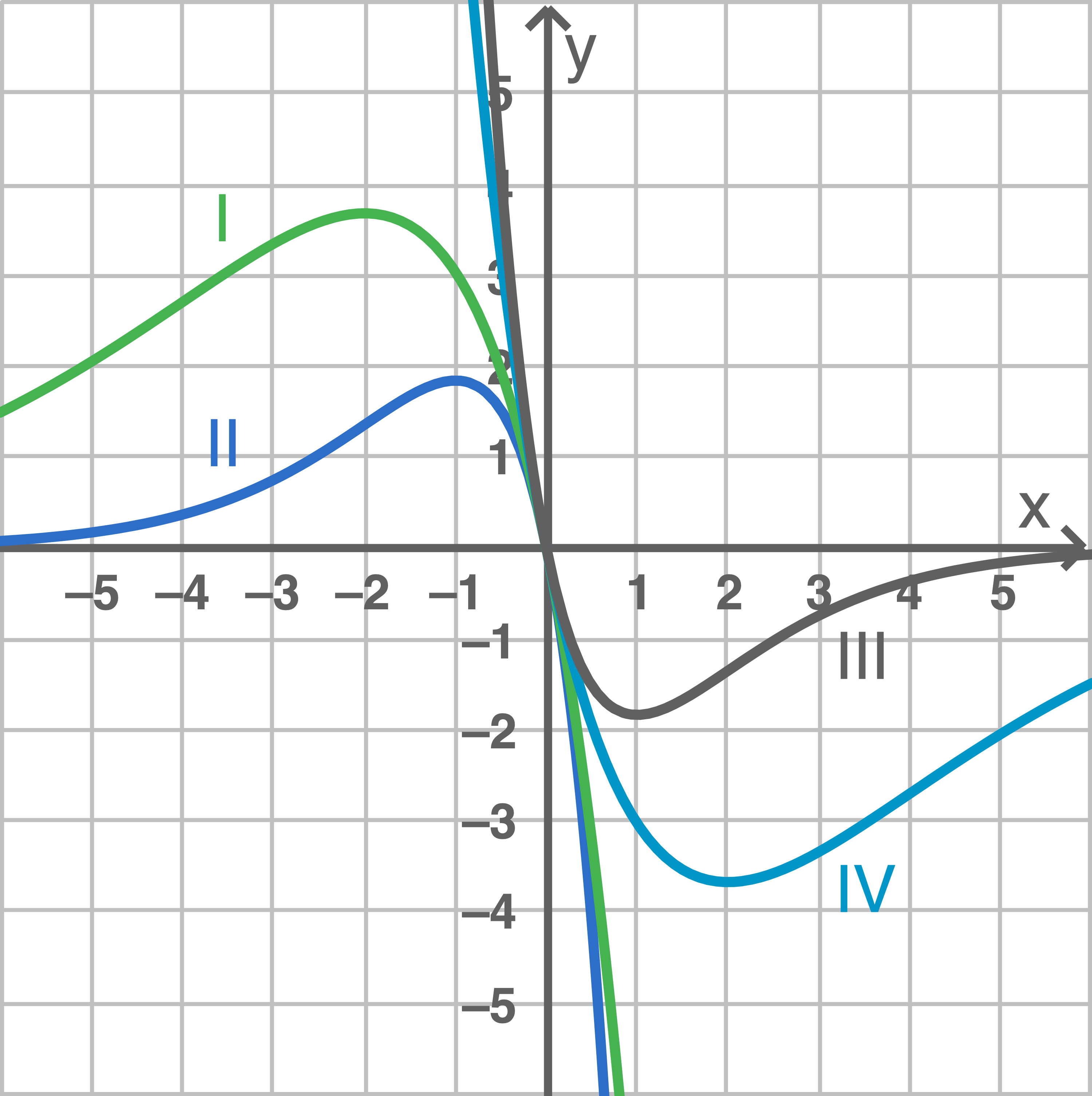
Abbildung 3 zeigt vier Graphen der Schar, die zu den Werten $k=-1, k=-0,5, k=0,5$ und $k=1$ gehören.

Der Graph III kann durch Spiegeln von $G$ (vgl. Abbildung 1) an der $x$ -Achse erzeugt werden. Gib den zugehörigen Wert von $k$ sowie die Koordinaten des Tiefpunkts von Graph III an. Ordne den drei übrigen Werten von $k$ den jeweils passenden Graphen zu.

(5 BE)

Zeige, dass $g_k(-x)=-g_{-k}(x)$ für alle $x \in \mathbb{R}$ gilt, und interpretiere diese Gleichung mit Blick auf die Graphen der Funktionen $g_k$ und $g_{-k}.$

(4 BE)

(30 BE)

Grafik mit vier Kurven in einem Koordinatensystem, beschriftet mit römischen Ziffern I bis IV.

Abb. 3

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Für die erste Ableitung von $f$ gilt:

$\(\begin{array}[t]{rlll} f$

Anwenden der notwendigen Bedingung für Extremstellen $\(f$ liefert:

$\(\begin{array}[t]{rlll} f$

Da die $\mathrm e$ -Funktion stets ungleich Null ist, folgt mit dem Satz des Nullprodukts:

$\begin{array}[t]{rlll} 5-5x&=&0 &\mid\;-5 \\[5pt] -5x&=&-5 &\mid\;:(-5) \\[5pt] x&=&1 \end{array}$

Aus der Aufgabenstellung folgt, dass die hinreichende Bedingung nicht überprüft werden muss. Einsetzen in $f$ ergibt:

$f(1)=5\cdot1\cdot\mathrm e^{-1}=\dfrac{5}{\mathrm e}$

Die Koordinaten des Extrempunkts von $G$ sind somit durch $\left(1\,\big\vert\,\frac{1}{\mathrm e}\right)$ gegeben.

Eine Gerade, die senkrecht zu $t$ verläuft, besitzt den negativen Kehrwert der Steigung von $t$ als Steigung. Einsetzen der Koordinaten des Extrempunkts in die allgemeine Gleichung einer solchen Geraden liefert:

$\begin{array}[t]{rlll} \dfrac{5}{\mathrm e}&=&\dfrac{\mathrm e^2}{5}\cdot1+n &\mid\;-\frac{\mathrm e^2}{5} \\[5pt] \dfrac{5}{\mathrm e}-\dfrac{\mathrm e^2}{5}&=&n \end{array}$

Für eine Gleichung der Gerade ergibt sich somit $y=\frac{\mathrm e^2}{5}x+\frac{5}{\mathrm e}-\frac{\mathrm e^2}{5}.$

Abbildung 1 zeigt, dass es verschiedene $x$ -Werte gibt, für die $f(x)$ denselben Wert annimmt. Damit kann $f$ nicht umkehrbar sein. Die Funktion $h$ ist jedoch umkehrbar, da $f$ ab der Extremstelle bei $x=1$ streng monoton fällt und somit keine Funktionswerte mehrfach angenommen werden.
Der Definitionsbereich der Umkehrfunktion von $h$ ist $\left] 0 ; \frac{5}{\mathrm{e}}\right]$ und der Wertebereich ist durch $[1 ;+\infty[$ gegeben.

Der Term $(5-\ln 5) \cdot \ln 5$ vorne in der Klammer gibt den Flächeninhalt eines Rechtecks der Breite $5-\ln 5$ und der Höhe $\ln 5$ an. Durch $\displaystyle\int_{\ln 5}^5 f(x)\;\mathrm d x$ ist der Inhalt des Flächenstücks gegeben, das $G$ zwischen $x=\ln 5$ und $x=5$ mit der $x$ -Achse einschließt.
Anordnen des Rechtecks in diesem Intervall zeigt, dass subtrahieren des Inhalts des durch das Integral gegebenen Flächenstücks vom Flächeninhalts des Rechtecks den Flächeninhalt der Fläche liefert, die zwischen $x=\ln 5$ und $x=5$ überhalb von $G$ liegt.
An der Geraden $y=x$ gespiegelt ist das genau die linke Hälfte des Wappens, das heißt somit ergibt der doppelte Wert des Ausdrucks in der Klammer den Flächeninhalt des ganzen Wappens.

Rechenweg anzeigen

$A \approx 6,1$

Der zu Graph III gehörende Wert von $k$ ist $k=1$ und die Koordinaten des Tiefpunkts ergeben sich mit Hilfe derer des Hochpunkts von $G$ als $\left(1\,\big\vert\,-\frac{1}{\mathrm e}\right).$
Zu Graph I gehört $k=-0,5,$ zu Graph II $k=-1$ und zu Graph IV $k=0,5.$

$\begin{array}[t]{rlll} g_k(-x)&=&-5 \cdot(-x) \cdot \mathrm e^{-k \cdot(-x)} \\[5pt] &=&-\left(-5 x \cdot \mathrm e^{-(-k) \cdot x}\right) \\[5pt] &=&-g_{-k}(x) \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?