Teil A

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=-\dfrac{1}{2} x^2+1.$

Zeichne den Graphen von $f$ für $-3 \leq x \leq 3$ in ein Koordinatensystem ein.

(2 BE)

Es gibt genau eine positive reelle Zahl $a,$ für die das Integral $\displaystyle\int_0^a f(x)\;\mathrm{d} x$ den Wert $0$ hat. Berechne $a.$

(3 BE)

Betrachtet wird eine in $\mathbb{R}$ definierte ganzrationale Funktion $g.$

Beschreibe, wie man rechnerisch nachweisen kann, dass $2$ eine Wendestelle von $g$ ist.

(2 BE)

Der Punkt $(2 \mid 3)$ ist der einzige Wendepunkt des Graphen von $g.$ Die in $\mathbb{R}$ definierte Funktion $h$ ist gegeben durch $h(x)=g(2x)-1.$

Gib die Koordinaten des Wendepunkts des Graphen von $h$ an und begründe deine Angabe.

(3 BE)

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=\dfrac{1}{4} x^3-3 x.$

Für die zweite Ableitungsfunktion von $f$ gilt $\(f$ Zeige, dass $2$ eine Extremstelle von $f$ ist.

(2 BE)

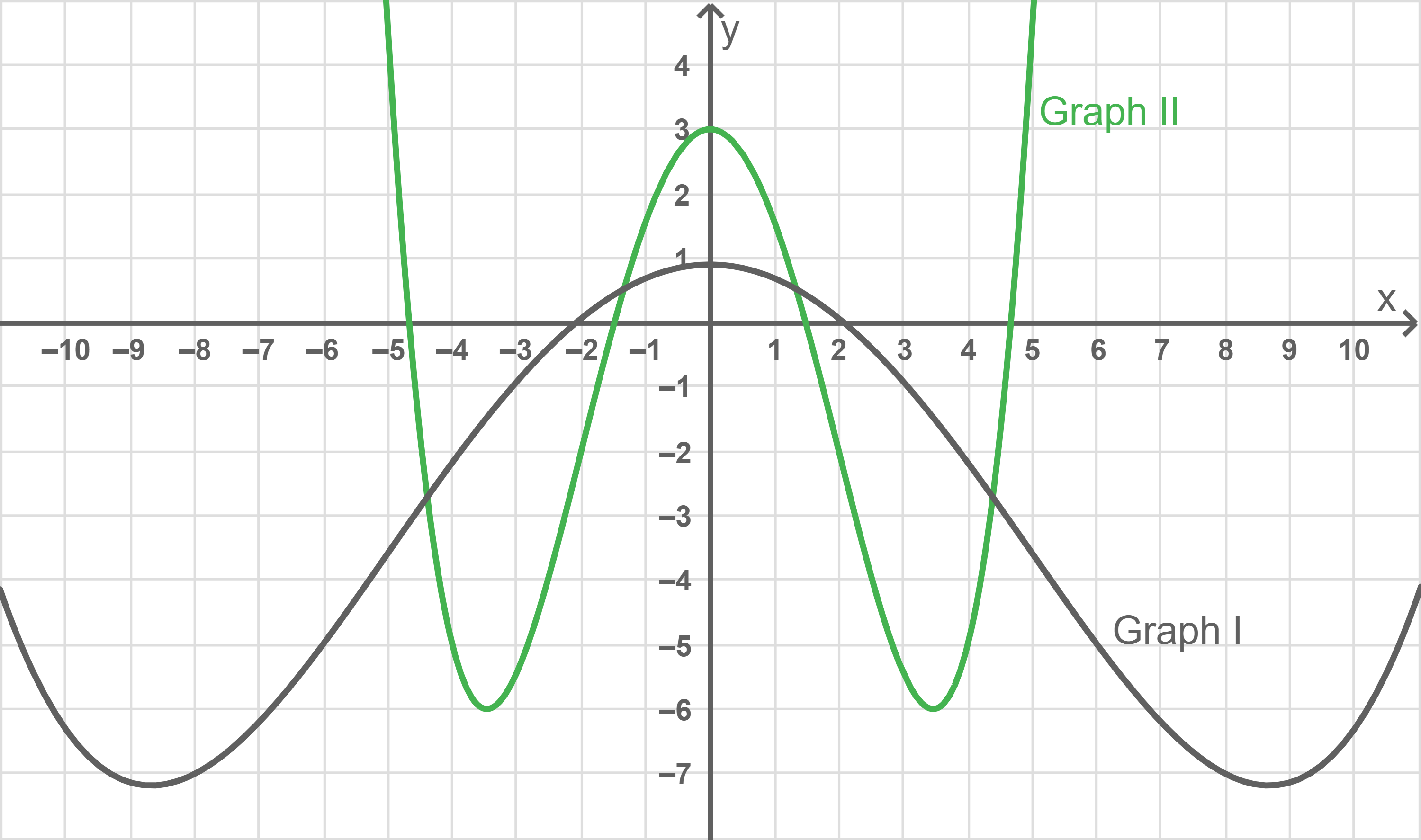
Einer der Graphen I und II in Abbildung 1 ist der Graph einer Stammfunktion von $f.$ Gib diesen Graphen an und begründe deine Angabe.

Abb. 1

(3 BE)

Gegeben ist die Funktion $g: x \mapsto \sqrt{x-2}$ mit $x \in[2 ;+\infty[.$
Die Abbildung zeigt den Graphen $G$ von $g$ sowie den Punkt $P(3\mid1).$
Die Gerade mit der Gleichung $y=\dfrac{1}{2}x-\dfrac{1}{2}$ ist die Tangente an $G$ im Punkt $P$ und hat mit $G$ nur den Punkt $P$ gemeinsam.

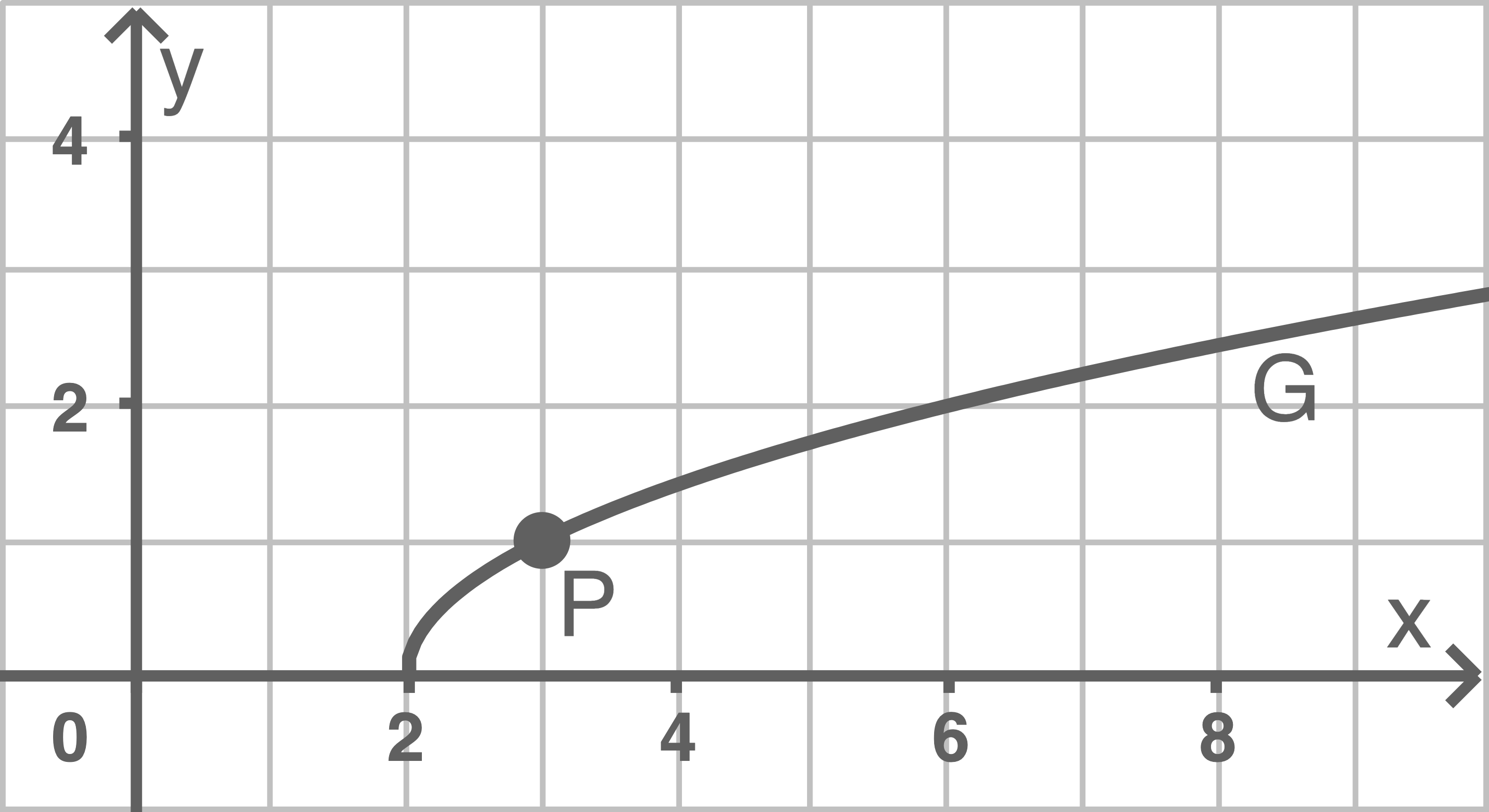
Graf mit einer Kurve und den Punkten P und G im Koordinatensystem. Achsen beschriftet mit x und y.

Abb. 2

Zeichne die Tangente in Abbildung 2 ein.

(1 BE)

Betrachtet wird eine Geraden, die mit $G$ sowohl den Punkt $P$ als auch einen weiteren Punkt gemeinsam hat.

Gib alle möglichen Steigungen dieser Geraden an.

(4 BE)

(20 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?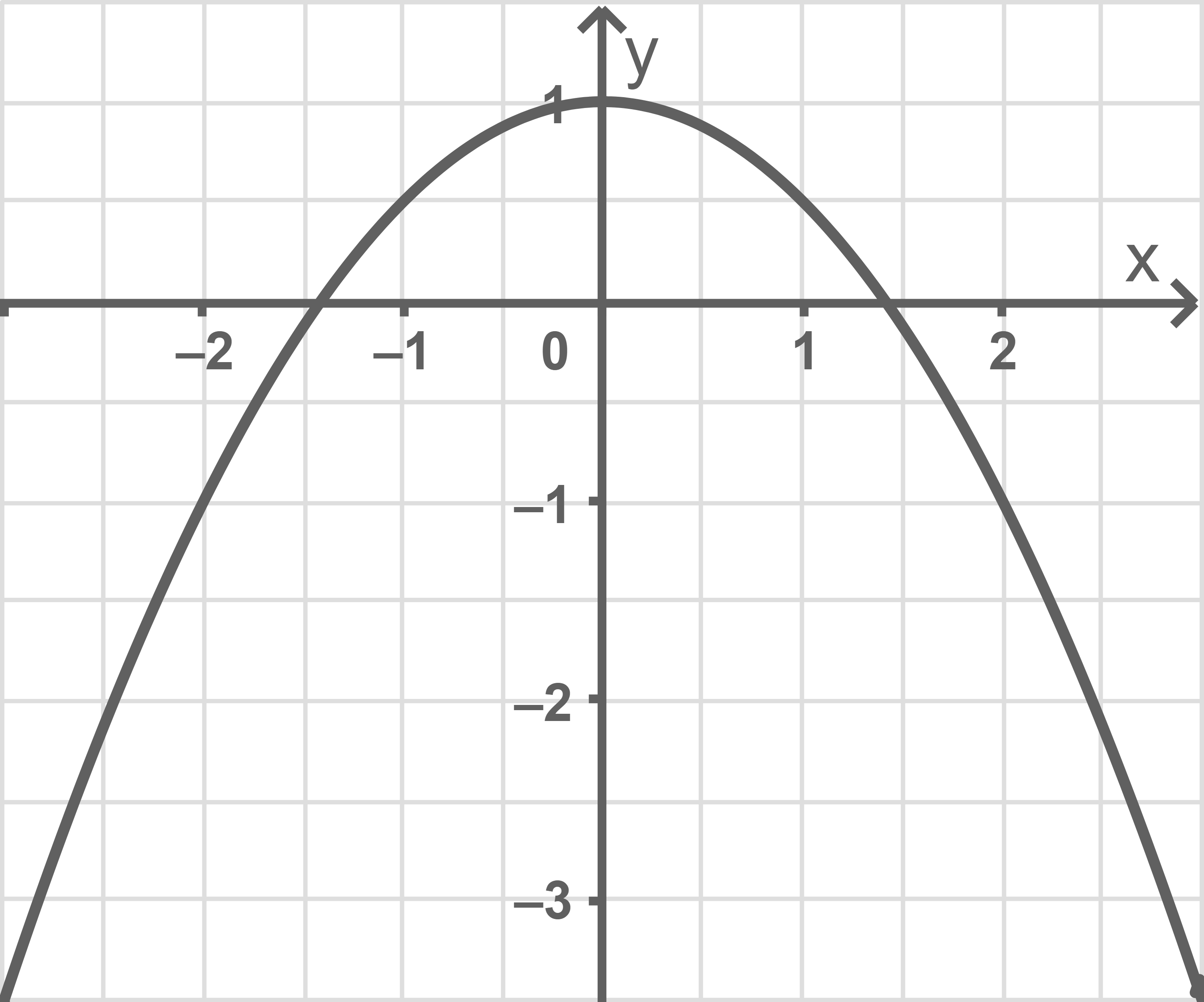

Graf einer Parabel mit Achsenbeschriftung x und y. Das Bild zeigt eine nach unten geöffnete Kurve.

$\begin{array}[t]{rlll} \displaystyle\int_{0}^{a}f(x)\;\mathrm dx&=&0 \\[5pt] \left[-\dfrac{1}{6} x^3+x\right]_0^a&=&0 \\[5pt] -\dfrac{1}{6} a^3+a&=&0 \\[5pt] a\cdot\left(-\dfrac{1}{6}a^2+1\right)&=&0 \end{array}$

Mit dem Satz des Nullprodukts folgt $a=0$ und weiter:

$\begin{array}[t]{rlll} -\dfrac{1}{6}a^2+1&=&0 &\mid\;-1 \\[5pt] -\dfrac{1}{6}a^2&=&-1 &\mid\;\cdot(-6) \\[5pt] a^2&=&6 &\mid\;\sqrt{\;} \\[5pt] a&=&\pm6 \end{array}$

Da $a\gt0$ gelten soll, folgt somit $a=6$ für den gesuchten Wert von $a.$

Es wird zunächst nachgewiesen, dass $\(g$ gilt. Außerdem muss die zweite Ableitung an dieser Stelle einen Vorzeichenwechsel besitzen. Wenn diese beiden Punkte erfüllt sind, handelt es sich um eine Wendestelle.

Koordinaten angeben

$W(1\mid2)$

Angabe begründen

Anhand der Funktionsgleichung lässt sich erkennen, dass der Graph von $h$ durch Streckung um den Faktor $\frac{1}{2}$ in $x$ -Richtung und Verschiebung um $1$ in $y$ -Richtung aus dem Graphen von $g$ hervorgeht.

Für die erste Ableitung von $f$ gilt:

$\(\begin{array}[t]{rlll} f$

Einsetzen von $x=2$ liefert:

$\(\begin{array}[t]{rlll} f$

Somit ist die notwendige Bendingung für Extremstellen in $x=2$ erfüllt. Da die hinreichende Bedingung für Extremstellen bereits in der Aufgabenstellung gegeben ist, folgt somit, dass $2$ eine Extremstelle von $f$ ist.

Da $f$ bei $x=2$ eine Extremstelle besitzt, hat jede Stammfunktion von $f$ bei $x=2$ eine Wendestelle. Aus der Abbildung folgt somit, dass Graph II der Graph einer Stammfunktion von $f$ ist.

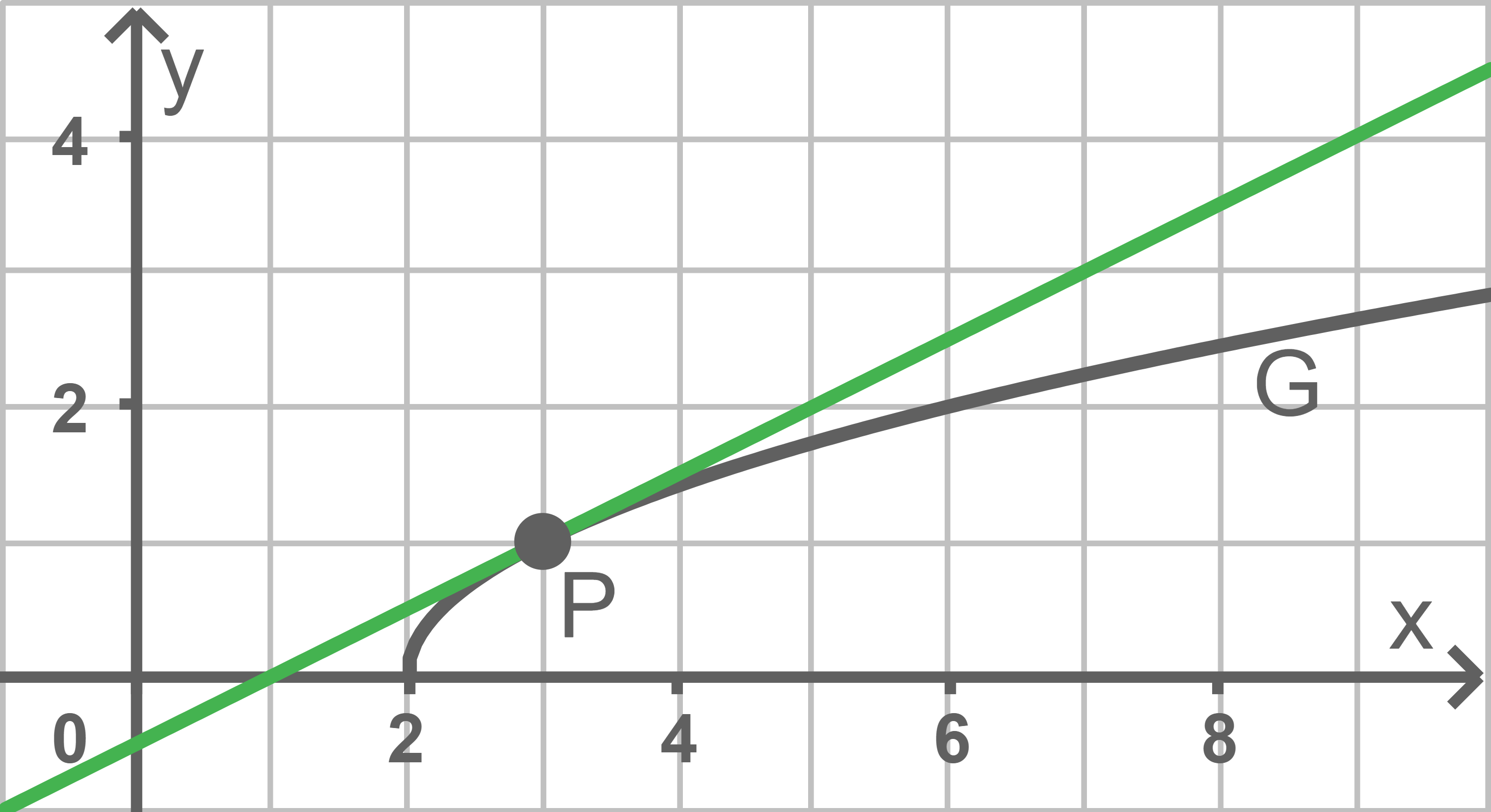
Diagramm mit zwei Kurven, einer grünen und einer grauen, im Koordinatensystem dargestellt. Punkt P ist markiert.

Für die Steigungen $m$ der Geraden mit der Eigenschaft aus der Aufgabenstellung gilt $\frac{1}{2}\lt m \leq 1$ oder $0\lt m\lt\frac{1}{2}.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?