Teil B

Badminton wird auf einem rechteckigen Spielfeld gespielt, das $13,40 \;\text{m}$ lang ist. Dabei wird ein Federball über ein $1,55 \;\text{m}$ hohes Netz geschlagen (vgl. Abbildung).

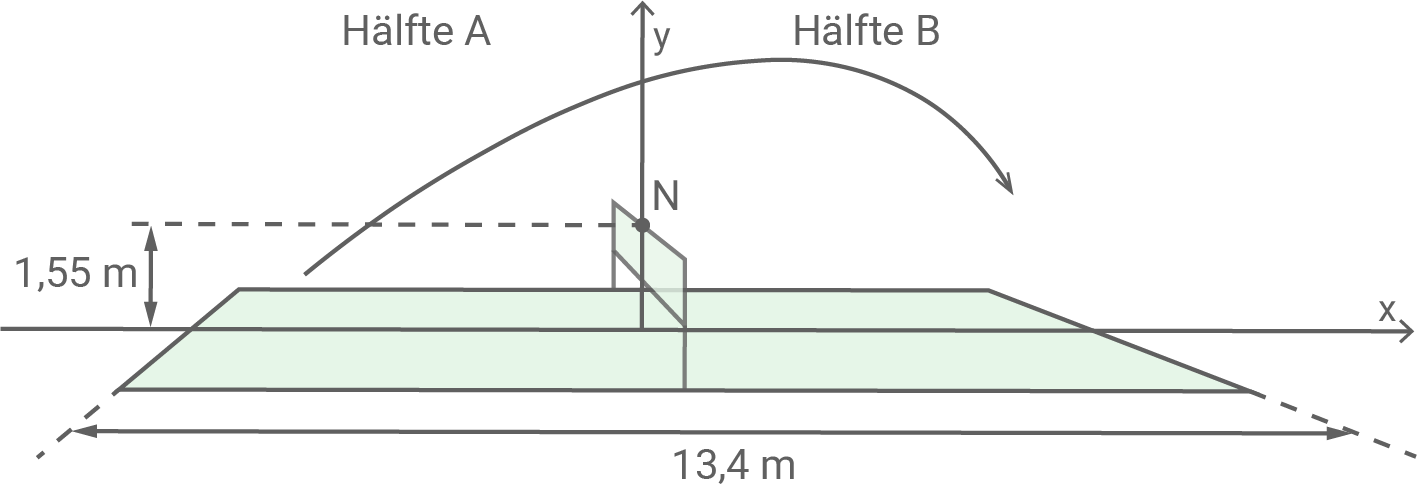
Diagramm mit einem Rechteck und Achsenbeschriftungen, zeigt Höhen und Längen in einem geometrischen Kontext.

Im Folgenden werden Flugbahnen von Federbällen, die von Hälfte $A$ in Hälfte $B$ des Spielfelds geschlagen werden, modellhaft mithilfe von Funktionen beschrieben. Vereinfachend werden nur Flugbahnen betrachtet, die innerhalb einer Ebene verlaufen, die senkrecht zum horizontalen Boden und parallel zur Seitenlinie des Spielfelds ist. Das im Modell verwendete Koordinatensystem liegt in dieser Ebene, wobei die $x$ -Achse den Boden und der Punkt $N(0 \mid 1,55)$ die horizontal verlaufende Oberkante des Netzes beschreibt. Eine Längeneinheit entspricht einem Meter in der Wirklichkeit.

Die in $]-\infty ; 6]$ definierte Funktion $f: x \mapsto 0,25 \cdot(x+6) \cdot \sqrt{6-x}$ beschreibt für $-5 \leq x \leq 6$ die Flugbahn bei einem bestimmten Schlag.

Gib die Koordinaten des Schnittpunkts des Graphen von $f$ mit der $y$ -Achse an und interpretiere das Ergebnis im Sachzusammenhang.

(2 BE)

Begründe, dass der Federball bei diesem Schlag innerhalb von Hälfte $B$ auf dem Boden auftrifft, wenn die Flugbahn nicht unterbrochen wird. Ein Spieler steht $3\;\text{m}$ hinter dem Netz in Hälfte $B$ unterhalb der Flugbahn des Federballs. Berechne die Höhe des Federballs über dem Boden an dieser Stelle.

(4 BE)

Weise nach, dass $\frac{6-3 x}{8 \cdot \sqrt{6-x}}$ ein Term der ersten Ableitungsfunktion $\(f$ von $f$ ist. Ermittle $\(\lim\limits_{x\to6}f$ und deute das Ergebnis im Sachzusammenhang.

(6 BE)

Im Verlauf des Flugs erreicht der Federball eine maximale Höhe.
Berechne diese.

(2 BE)

Bei einem anderen Schlag wird die Flugbahn des Federballs für $-0,25 \leq x \leq 1$ mithilfe der in $\mathbb{R}$ definierten Funktion $g: x \mapsto-2 x+2$ beschrieben.

Zeige unter Verwendung einer geeigneten Skizze, dass die Entfernung eines beliebigen Punkts $Q(x\mid g(x))$ auf dem Graphen von $g$ zum Punkt $N(0 \mid 1,55)$ durch den Term $d(x)=\sqrt{5 x^2-1,8 x+0,2025}$ beschrieben werden kann.

(5 BE)

Auf dieser Flugbahn gibt es einen Punkt mit minimalem Abstand zur oberen Netzkante. Berechne diesen minimalen Abstand.

(3 BE)

Im Folgenden werden Schläge betrachtet, bei denen die Flugbahn des Federballs jeweils mithilfe einer Funktion $h: x \mapsto a \cdot \sqrt{b-x}+c$ mit maximalem Definitionsbereich und $a, b, c \in \mathbb{R}$ beschrieben wird.

Ermittle für $a=2, b=5$ und $c=-2,$ in welcher Entfernung zur Netzebene und unter welchem Winkel der Federball auf dem Boden auftrifft.

(4 BE)

Ein Federball wird von einem Spieler in Hälfte $A$ im Abstand von $1\;\text{m}$ zur Netzebene in einer Höhe von $2,60\;\text{m}$ geschlagen und trifft im Abstand von $3\;\text{m}$ zur Netzebene in Hälfte $B$ senkrecht zum Boden auf diesem auf.
Ermittle die zugehörigen Werte von $a, b$ und $c.$

(4 BE)

(30 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Koordinaten angeben

$\begin{array}[t]{rlll} f(0)&=&0,25\cdot(0+6)\cdot\sqrt{6-0} \\[5pt] &\approx&3,67 \end{array}$

Die Koordinaten des Schnittpunkts mit der $y$ -Achse sind somit durch $S_y(0\mid3,67)$ gegeben.

Ergebnis interpretieren

Der Federball überquert das Netz in einer Höhe von ca. $3,67\;\text{m}$ über dem Boden und fliegt somit hoch über dem Netz.

$\begin{array}[t]{rlll} f(x)&=&0 \\[5pt] 0,25\cdot(x+6)\cdot\sqrt{6-x}&=&0 \end{array}$

Mit dem Satz des Nullprodukts folgt, dass die Nullstellen von $f$ durch $x_1=-6$ und $x_2=6$ gegeben sind. Da eine Hälfte des Feldes $\frac{13,4}{2}=6,7\;\text{m}$ lang ist, trifft der Ball rechts vom Netz somit innerhalb des Feldes auf den Boden.
Für die gesuchte Höhe $3\;\text{m}$ hinter dem Netz in Hälfte $B$ gilt zudem:

$\begin{array}[t]{rlll} f(3)&=&0,25\cdot(3+6)\cdot\sqrt{6-3} \\[5pt] &\approx&3,9\;[\text{m}] \end{array}$

Ableitungsfunktion nachweisen

Für die Ableitung von $f$ folgt mit der Produkt- und Kettenregel:

Rechenweg anzeigen

$\( f$

Grenzwert ermitteln und deuten

Für $x\rightarrow6$ geht der Nenner gegen Null und der Zähler gegen $-12.$ Somit gilt:

$\lim\limits_{x\to6}f(x)=-\infty$

Im Sachzusammenhang bedeutet dass, dass der Federball am Ende der Flugbahn sehr steil fällt und senkrecht auf dem Boden auftrifft.

$\(\begin{array}[t]{rlll} f$

Auf das Überprüfen der hinreichenden Bedingung für Extremstellen kann verzichtet werden, da die Aufgabenstellung sagt, dass $f$ einen Hochpunkt besitzt. Einsetzen von $x=2$ in $f(x)$ liefert für die gesuchte Höhe:

$\begin{array}[t]{rlll} f(2)&=&0,25 \cdot(2+6) \cdot \sqrt{6-2} \\[5pt] &=&4\;[\text{m}] \end{array}$

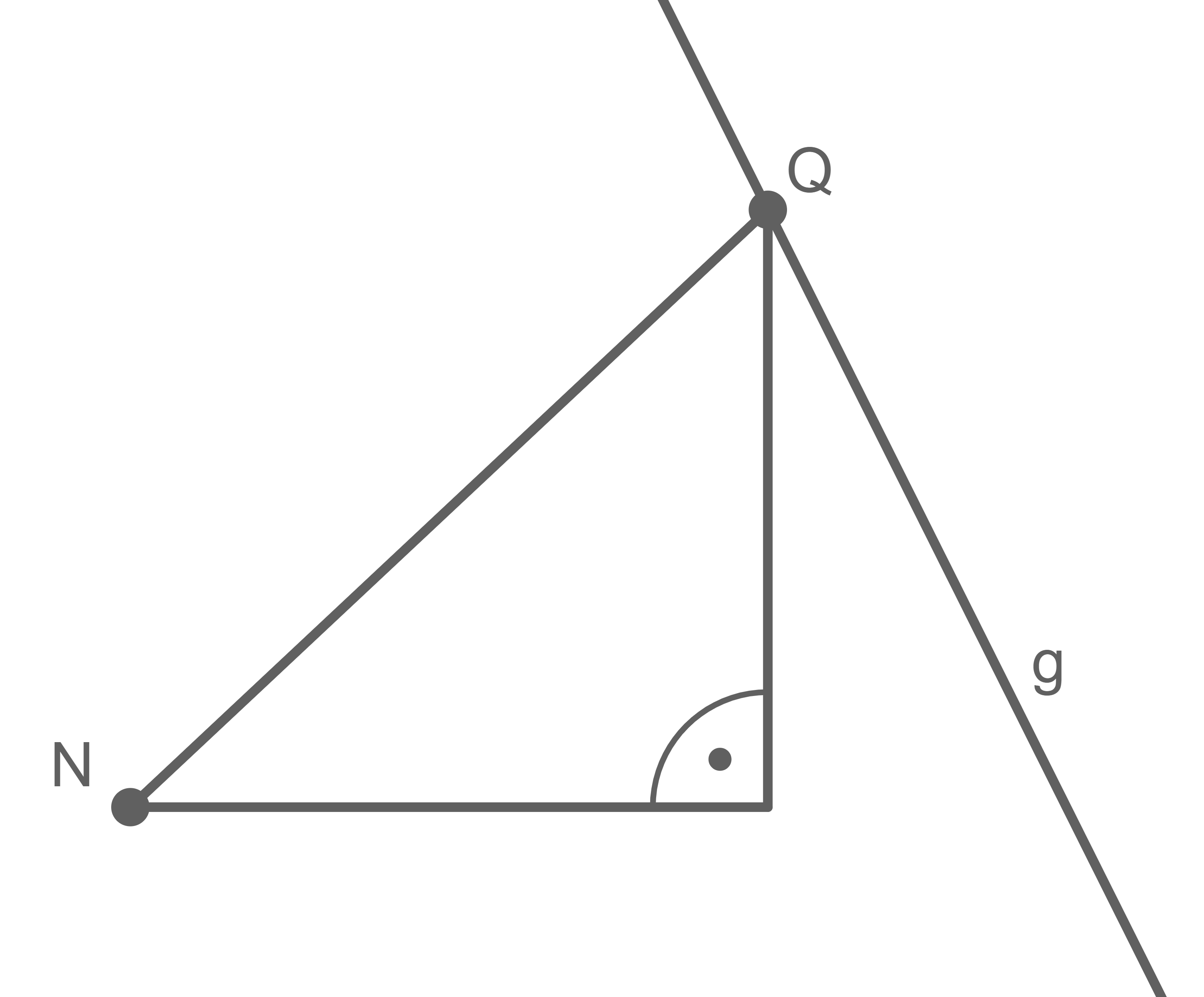
Geometrische Darstellung eines rechtwinkligen Dreiecks mit beschrifteten Punkten und einer Linie.

Die Skizze zeigt, dass der Abstand von $N$ zu $Q$ mit Hilfe des Satzes des Pythagoras wie folgt gegeben ist:

$\begin{array}[t]{rlll} d(x)&=&\sqrt{(x-0)^2+(g(x)-1,55)^2} \\[5pt] &=&\sqrt{x^2+(-2x+0,45)^2} \\[5pt] &=&\sqrt{x^2+(-2x+0,45)^2} \\[5pt] &=&\sqrt{5 x^2-1,8 x+0,2025} \end{array}$

Für die erste Ableitung von $d(x)$ gilt:

Rechenweg anzeigen

$\( d$

Nullsetzen liefert:

$\(\begin{array}[t]{rlll} d$

Auf das Überprüfen der hinreichenden Bedingung für Extremstellen kann verzichtet werden, da die Aufgabenstellung sagt, dass $d$ einen Tiefpunkt besitzt. Einsetzen von $x=0,18$ in $d(x)$ liefert für den gesuchten Abstand:

Rechenweg anzeigen

$d(0,18) \approx 0,2$

Der gesuchte Abstand beträgt somit ca. $0,2\;\text{m}.$

$\begin{array}[t]{rlll} h(x)&=&0 \\[5pt] 2\cdot\sqrt{5-x}-2&=&0 &\mid\;+2 \\[5pt] 2\cdot\sqrt{5-x}&=&2 &\mid\;^2 \\[5pt] 20-4x&=&4 &\mid\;-20 \\[5pt] -4x&=&-16 &\mid\;:(-4) \\[5pt] x&=&4 \end{array}$

Für die Ableitung von $h$ gilt:

$\(\begin{array}[t]{rlll} h$

Einsetzen der Nullstelle in die Ableitungsfunktion liefert:

$\(\begin{array}[t]{rlll} h$

Der Federball trifft somit $4\;\text{m}$ vom Netz entfernt in einem Winkel von $45^\circ$ auf dem Boden auf.

Dass der Ball senkrecht auf dem Boden auftrifft, bedeutet, dass $\(h$ dort den Wert $-\infty$ annimmt. Da $\(h$ die Ableitung der allgemeinen Funktion $h$ ist, muss $b$ der Nullstelle entsprechen und es folgt damit $b=3.$ Mit den Bedingungen aus der Aufgabenstellung folgt weiter:

$\begin{array}[t]{rlll} h(3)&=&0 \\[5pt] a\cdot\sqrt{3-3}+c&=&0 \\[5pt] c&=&0 \end{array}$

$\begin{array}[t]{rlll} h(-1)&=&2,6 \\[5pt] a\cdot\sqrt{3-(-1)}&=&2,6 &\mid\;:2 \\[5pt] a&=&1,3 \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?