Teil B

Gegeben sind die Punkte $A(30\mid-5\mid-12), B(30\mid13\mid 0),$ $C(-30\mid13\mid 0)$ und $D(-30\mid-5\mid-12),$ die in der Ebene $E$ liegen.

Begründe, dass das Viereck $ABCD$ ein Rechteck ist.

(3 BE)

Bestimme eine Gleichung von $E$ in Koordinatenform und gib die besondere Lage von $E$ im Koordinatensystem an.

(zur Kontrolle: $E: 2 x_2-3 x_3-26=0$ )

(3 BE)

Bestimme die Größe $\varphi$ des Winkels, den $E$ mit der $x_1 x_2$ -Ebene einschließt.

(zur Kontrolle: $\varphi \approx 33,7^{\circ}$ )

(3 BE)

Im Folgenden wird ein Sperrwerk an einem Fluss betrachtet, das dem Schutz vor Überflutungen bei Sturmfluten dient. Ein Teil dieses Sperrwerks besteht aus zwei kreisförmigen Metallscheiben, an denen ein Sperrtor befestigt ist. Durch Drehung der Metallscheiben wird das Sperrtor in verschiedene Stellungen gebracht.

In einem Koordinatensystem werden die beiden Metallscheiben durch die Grund- und Deckfläche eines geraden Zylinders dargestellt. Die $x_1$ -Achse verläuft durch die Mittelpunkte dieser beiden Kreisflächen und entspricht der Drehachse der Metallscheiben.

Die Ebene $E$ schneidet den Zylinder im Rechteck $ABCD$ und zerlegt diesen in zwei Teilkörper. Der kleinere Teilkörper entspricht dem Sperrtor in einer speziellen Stellung (vgl. Abbildung 1). Eine Längeneinheit entspricht einem Meter in der Realität.

Es wird vereinfachend ausschließlich ein Wasserstand betrachtet, bei dem die Wasseroberfläche im Modell in der $x_1 x_2$ -Ebene liegt.

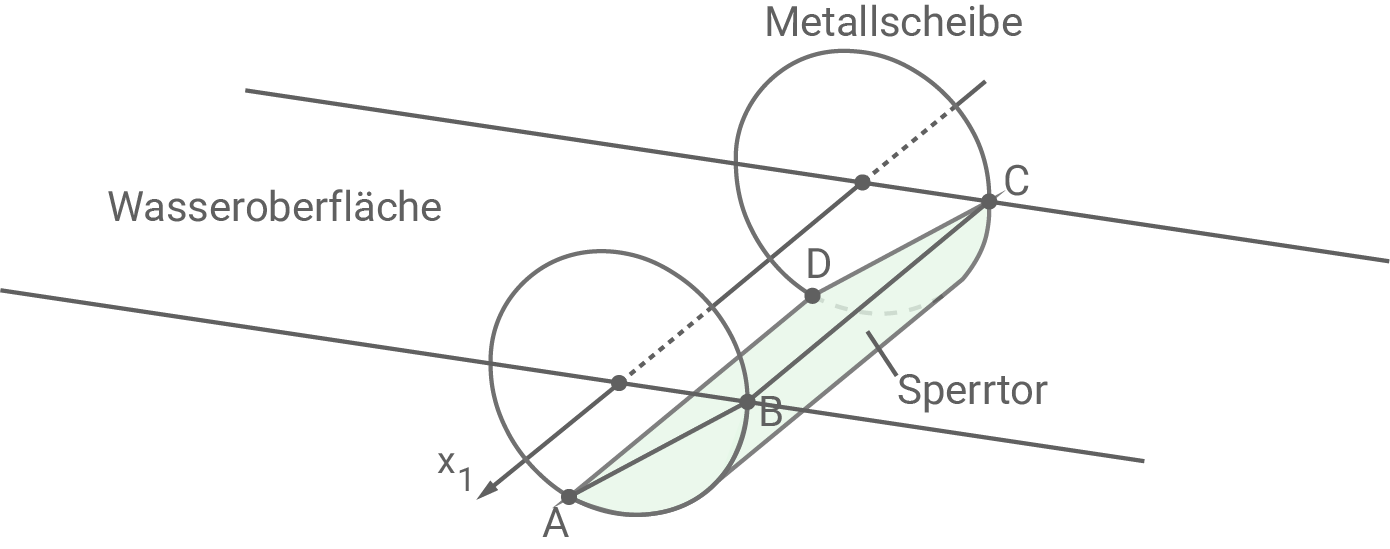
Diagramm mit Wasseroberfläche, Metallscheibe und geometrischen Elementen zur Darstellung physikalischer Konzepte.

Abb. 1

Gib den Durchmesser einer Metallscheibe und den Abstand der beiden Metallscheiben jeweils in Metern an.

(2 BE)

Ist das Sperrtor geöffnet, so liegt dessen rechteckige Seitenfläche unterhalb der Wasseroberfläche und ist parallel zu ihr (vgl. Abbildung 2a). Ist das Sperrtor geschlossen, so steht die Seitenfläche senkrecht zur Wasseroberfläche (vgl. Abbildung 2b).

Diagramm mit Wasseroberfläche und geöffnetem Sperrtor.

Abb. 2a

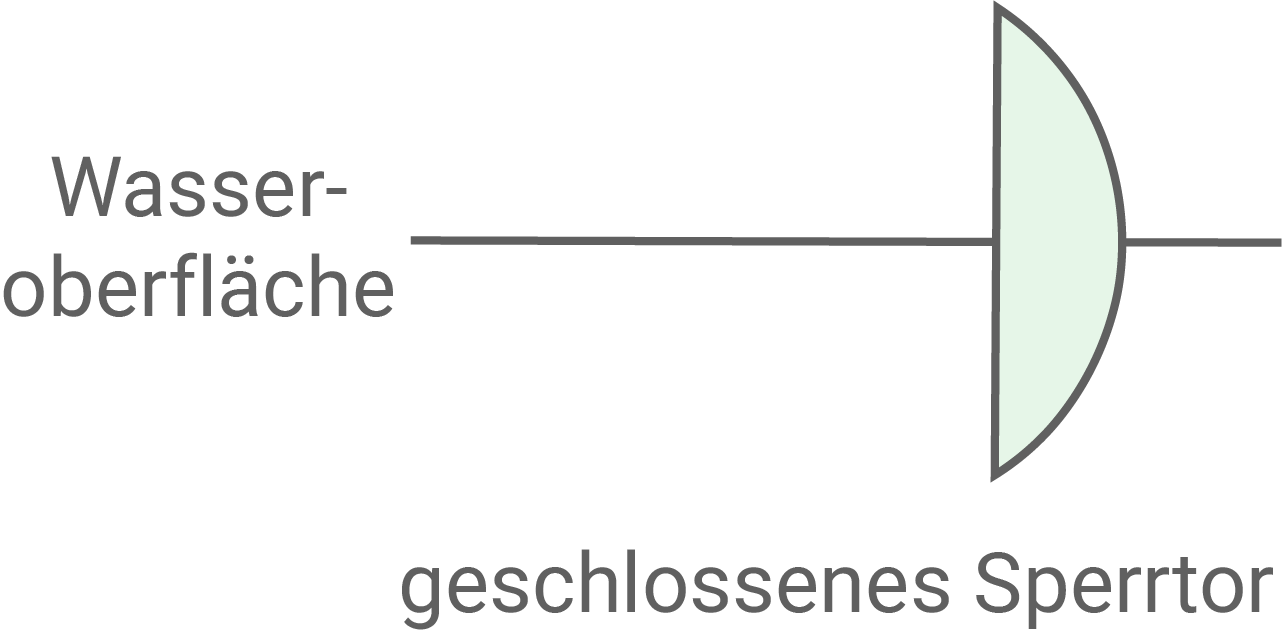
Illustration einer Wasseroberfläche mit einem geschlossenen Sperrtor.

Abb. 2b

Bei einem Schließvorgang wird das geöffnete Sperrtor durch eine Vierteldrehung der Metallscheiben mit konstanter Geschwindigkeit innerhalb von $15$ Minuten geschlossen.

Zu einem bestimmten Zeitpunkt während des Schließvorgangs befinden sich erstmals Teile des Sperrtors an der Wasseroberfläche. Bestimme mithilfe des Ergebnisses von Aufgabe c die Zeit, die ab diesem Zeitpunkt bis zum Ende des Schließvorgangs vergeht. Ermittle, wie weit das geschlossene Sperrtor über die Wasseroberfläche hinausragt.

(4 BE)

Die tiefste Stelle eines Schiffs bewegt sich im Modell auf der Gerade $g: \overrightarrow{x}=\pmatrix{0\\-17\\-8}+\lambda \cdot\pmatrix{0\\1\\0}, \lambda \in \mathbb{R}.$ Beurteile anhand einer Rechnung, ob das Schiff das Sperrwerk passieren kann, wenn das Sperrtor geöffnet ist.

(5 BE)

(20 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$\begin{array}[t]{rlll} \overrightarrow{AB}&=&\pmatrix{30\\13\\0}-\pmatrix{30\\-5\\-12} \\[5pt] &=&\pmatrix{0\\18\\12} \end{array}$

$\begin{array}[t]{rlll} \overrightarrow{DC}&=&\pmatrix{-30\\13\\0}-\pmatrix{-30\\-5\\-12} \\[5pt] &=&\pmatrix{0\\18\\12} \end{array}$

Damit sind die beiden zugehörigen, gegenüberliegenden Kanten parallel zueinander. Außerdem gilt:

$\begin{array}[t]{rlll} \overrightarrow{AB}\circ\overrightarrow{AD}&=&\pmatrix{0\\18\\12}\circ\pmatrix{-30-30\\-5-(-5)\\-12-(-12)} \\[5pt] &=&\pmatrix{0\\18\\12}\circ\pmatrix{-60\\0\\0} \\[5pt] &=&0 \end{array}$

Da das Viereck $ABCD$ somit zusätzlich in $A$ einen rechten Winkel besitzt, ist es sogar ein Rechteck.

$\begin{array}[t]{rlll} \overrightarrow{n}&=&\overrightarrow{AB}\times\overrightarrow{AD} \\[5pt] &=&\pmatrix{0\\18\\12}\times\pmatrix{-60\\0\\0} \\[5pt] &=&\pmatrix{0\\-720\\1080} \end{array}$

Mit dem Normalenvektor $-\frac{1}{360}\cdot\overrightarrow{n}$ ergibt sich:

$E:2x_2-3x_3-d=0$

Einsetzen der Koordinaten von z.B. $A$ liefert für $d:$

$\begin{array}[t]{rlll} 2\cdot(-5)-3\cdot(-12)-d&=&0 \\[5pt] -10+36-d&=&0 &\mid\;+d \\[5pt] 26&=&d \end{array}$

Eine Ebenengleichung von $E$ in Koordinatenform ist somit durch $E:2x_2-3x_3-26=0$ gegeben. Da die Ebenengleichung $x_1$ nicht enthält, verläuft $E$ parallel zur $x_1$ -Achse.

Mit $\pmatrix{0\\0\\1}$ als Normalenvektor der $x_1x_2$ -Ebene folgt:

$\begin{array}[t]{rlll} \cos(\varphi)&=&\dfrac{\left\vert\pmatrix{0\\2\\-3}\circ\pmatrix{0\\0\\1}\right\vert}{\left\vert\pmatrix{0\\2\\-3}\right\vert\cdot\left\vert\pmatrix{0\\0\\1}\right\vert} \\[5pt] \cos(\varphi)&=&\dfrac{\left\vert-3\right\vert}{\sqrt{2^2+(-3)^2}\cdot\sqrt{1}} \\[5pt] \cos(\varphi)&=&\dfrac{3}{\sqrt{13}} \\[5pt] \varphi&=&\cos^{-1}\left(\dfrac{3}{\sqrt{13}}\right) \\[5pt] \varphi&\approx&33,7^\circ \end{array}$

Der Radius der Metallscheiben ist durch den Abstand von $A$ und $B$ zur $x_1$ -Achse gegeben. Da $B$ sich von einem Punkt auf der $x_1$ -Achse nur in der $x_2$ -Koordinate unterscheidet, ist der Abstand zu der $x_1$ -Achse durch diesen Wert gegeben, also $13\;\text{m}.$ Der Durchmesser einer Metallscheibe beträgt somit $26\;\text{m}.$
Der Abstand der beiden Metallscheiben zueinander ist durch die Länge des Vektors $\overrightarrow{AD}$ gegeben, d.h. für ihn folgt:

$\begin{array}[t]{rlll} \left\vert\overrightarrow{AD}\right\vert&=&\left\vert\pmatrix{-60\\0\\0}\right\vert \\[5pt] &=&\sqrt{(-60)^2} \\[5pt] &=&60\;[\text{m}] \end{array}$

Im geschlossenen Zustand steht das Sperrtor in einem Winkel von $90^\circ$ zur Wasseroberfläche. Aus den Abbildungen lässt sich erkennen, dass das Sperrtor genau dann die Wasseroberfläche durchstößt, wenn es in der Position in Abbildung 1 steht, das heißt wenn die glatte Oberfläche des Tors in der Ebene $E$ liegt und somit den Winkel aus Aufgabenteil c) zur Wasseroberfläche besitzt. Da der komplette Schließvorgang $15$ Minuten dauert, folgt für die gesuchte Zeit:

$\dfrac{90^\circ-33,7^\circ}{90^\circ}\cdot15\approx9,38\;\text{min}$

Mit $0,38\cdot60\approx23$ folgt, dass die gesuchte Zeit $9$ Minuten und $23$ Sekunden beträgt.
Im geschlossenen Zustand steht das Sperrtor senkrecht zur Wasseroberfläche und ragt somit um die Länge des Radius darüber hinaus. Da dieser $13\;\text{m}$ beträgt, ist das die gesuchte Strecke.

Bei der Drehung des Sperrtors ändert sich der Abstand zur $x_1$ -Achse nicht. Da die Ebene $E$ parallel zur $x_1$ -Achse verläuft, ist dieser somit immer durch den Abstand des Koordinatenursprungs zur Ebene $E$ gegeben. Mit der Hesseschen Normalform folgt für diesen:

$E:\dfrac{1}{\sqrt{2^2+(-3)^2}}\cdot\left\vert2\cdot0-3\cdot0-26\right\vert$ $\approx7,2\;[\text{m}]$

Im geöffneten Zustand liegt das Sperrtor mit der flachen Oberseite nach oben im Wasser, und damit ca. $7,2\;\text{m}$ unter der Wasseroberfläche. Da der Richtungvektor der Geraden $g$ keine $x_3$ -Komponente besitzt, ist die Höhe der tiefsten Stelle der Schiffs konstant durch die $x_3$ -Komponente des Stützvektors von $g$ gegeben und liegt damit $8\;\text{m}$ unter der Wasseroberfläche.
Somit kann das Schiff das Sperrwerk nicht passieren, wenn das Sperrtor geöffnet ist.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?