B6 – Geometrie
Gegeben sind die Punkte 
und 
Zeige, dass das Dreieck 
gleichschenklig ist.
Begründe, dass 
und 
Eckpunkte eines Quadrats sein können, und gib die Koordinaten des vierten Eckpunkts 
dieses Quadrats an.
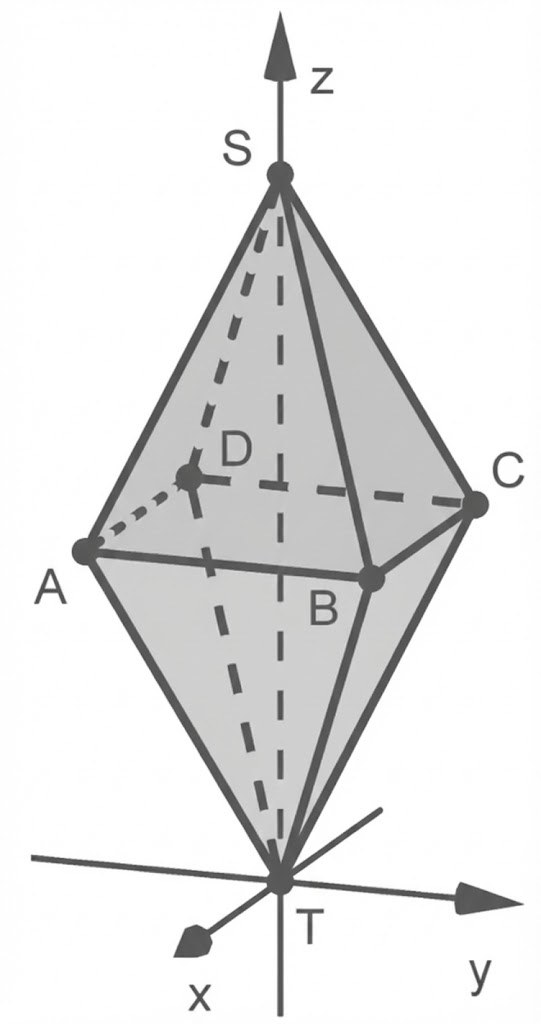
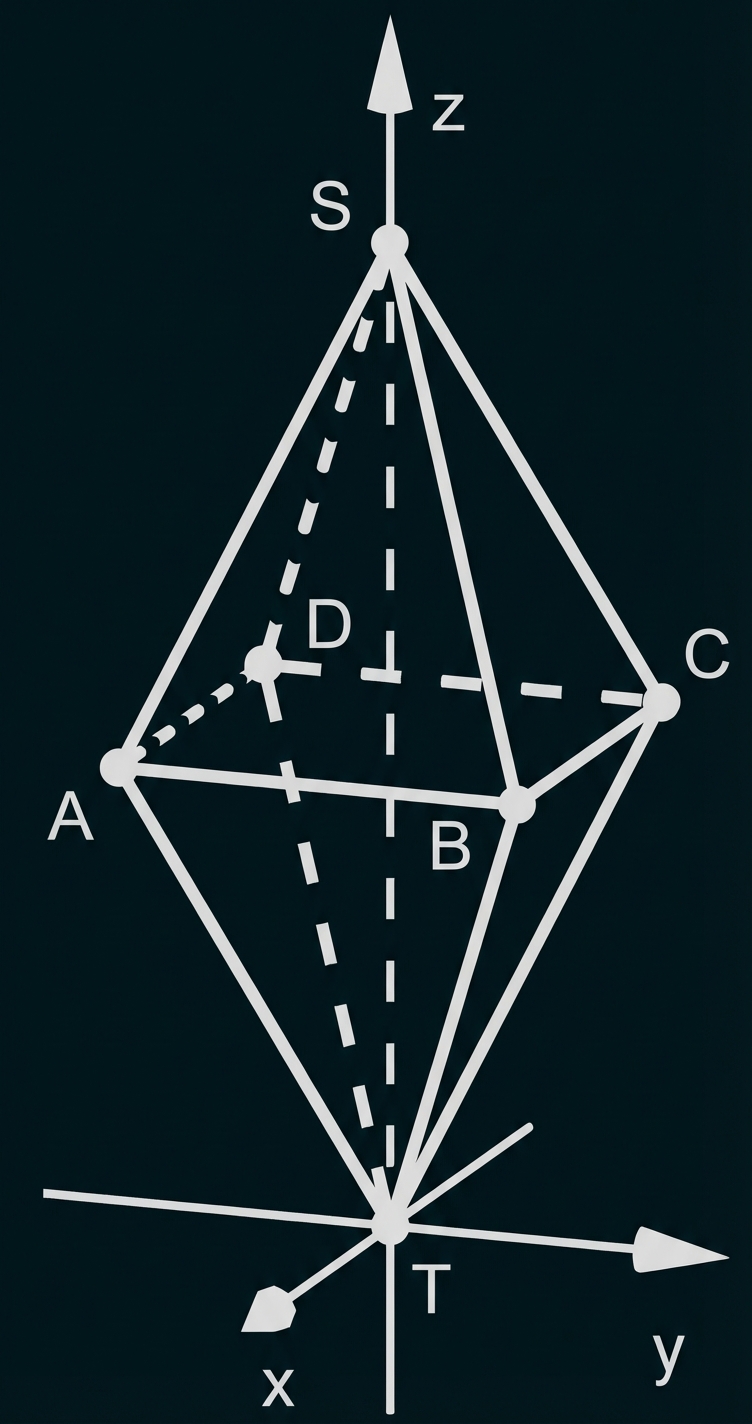
Im Folgenden wird die Doppelpyramide in Abbildung 1 betrachtet. Die beiden Teilpyramiden 
und 
sind gleich hoch. Der Punkt 
liegt im Koordinatenursprung, der Punkt 
ebenfalls auf der 
-Achse.
Die Seitenfläche 
liegt in einer Ebene 
Bestimme eine Gleichung von 
in Koordinatenform.
(zur Kontrolle: 
)
Bestimme die Größe des Winkels, den die Seitenfläche mit der Fläche 
einschließt.
gehört zur Schar der Ebenen 
mit 
Die Strecke 
liegt auf jeder Ebene dieser Schar.
Ermittle diejenigen Werte von 
für die 
mit der Seitenfläche 
mindestens einen Punkt gemeinsam hat.
Die Seitenfläche 
liegt in der Ebene 
Gib einen Normalenvektor von 
an und begründe deine Angabe, ohne die Koordinaten von 
und zu verwenden. Bestimme denjenigen Wert von für den senkrecht zu steht.
Die Doppelpyramide wird so um die 
-Achse gedreht, dass die Seitenfläche in eine Fläche übergeht, die in der 
-Ebene liegt, und der Punkt in einen Punkt 
der eine positive 
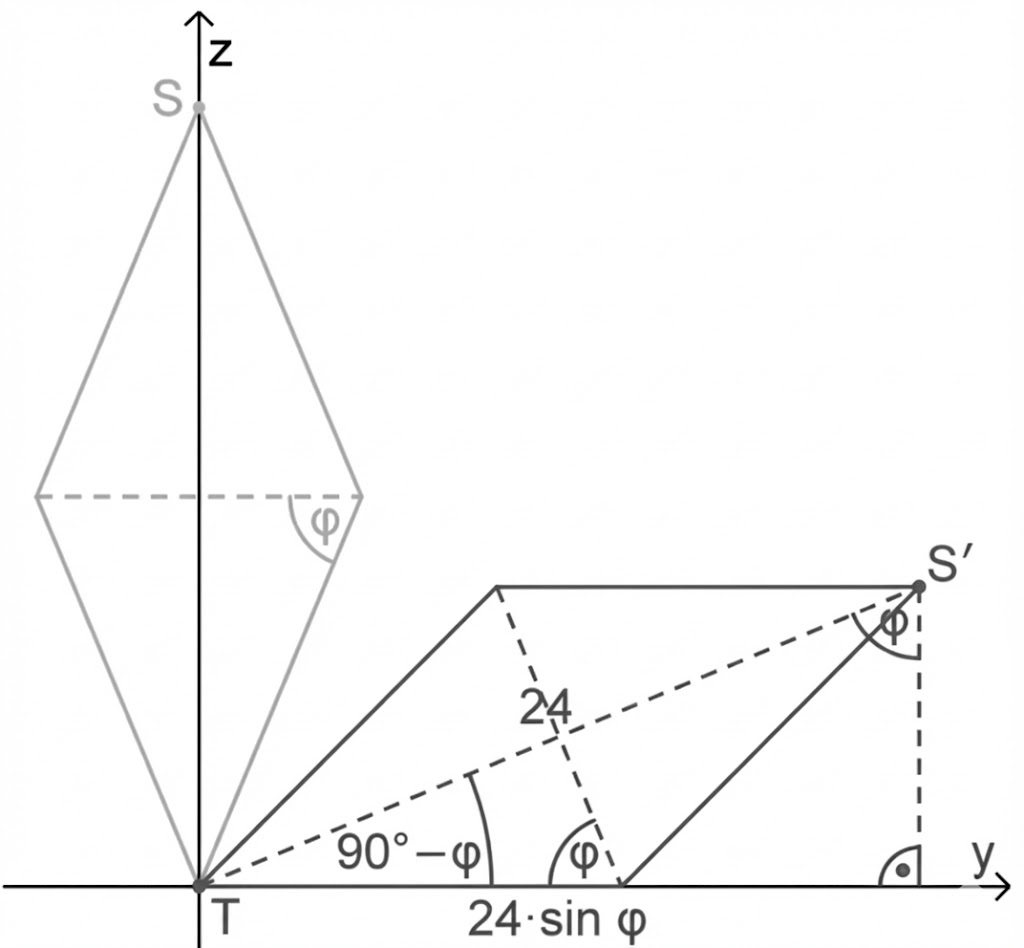
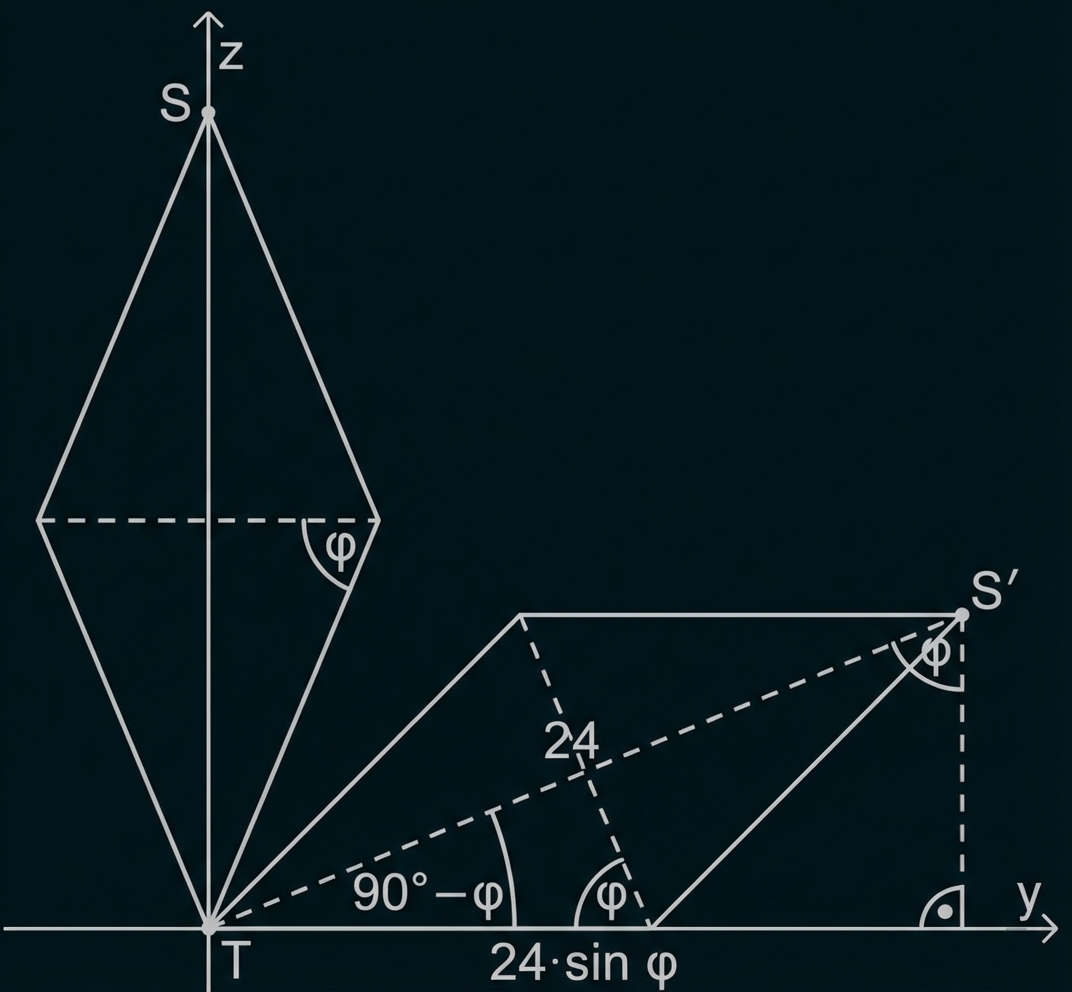
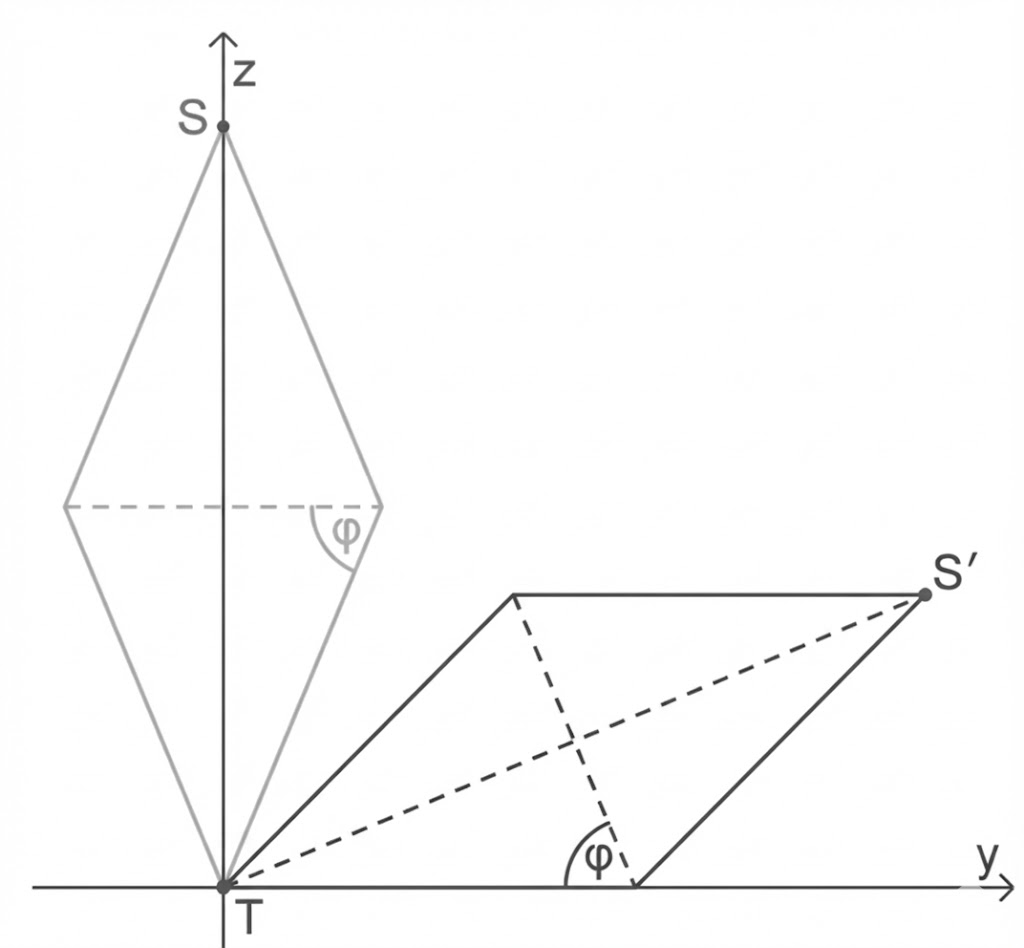
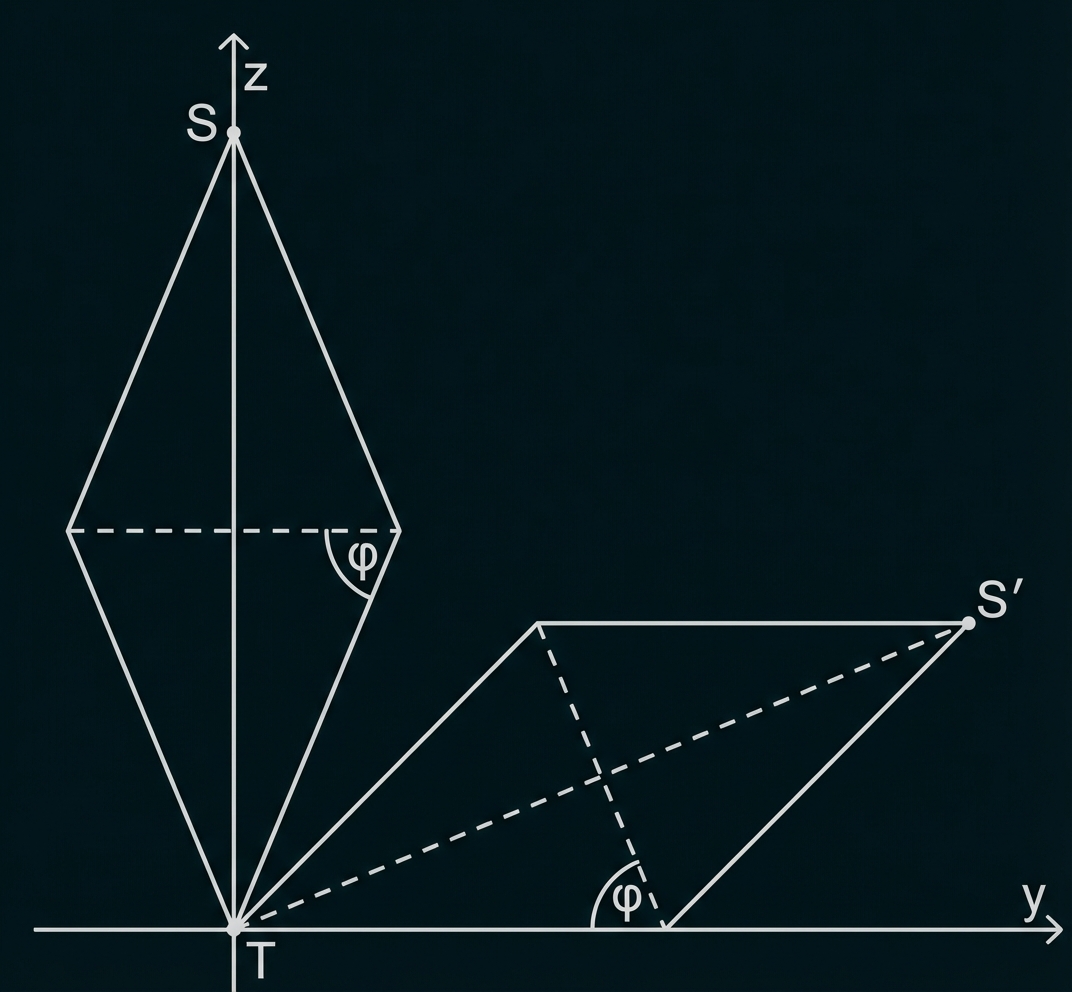
-Koordinate hat. Abbildung 2 zeigt jeweils einen Längsschnitt der Doppelpyramide durch die 
-Ebene vor und nach dieser Drehung.
Begründe anhand geeigneter Eintragungen in Abbildung 2, dass die -Koordinate von den Wert 
hat, wobei 
die in Aufgabe c bestimmte Winkelgröße ist.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
Somit gilt 
d.h. das Dreieck ist gleichschenklig.
![Formula: \begin{array}[t]{rll} \overrightarrow{BC} \times \overrightarrow{BT}&=&\pmatrix{0\\-120\\50} \\[5pt] &=&-10 \cdot\pmatrix{0\\-12\\5} \end{array}](https://www.schullv.de/resources/formulas/fba840e18e3a780ec1ee92b5f4213a9a961fa8f4357bf5d938913a22de2273d9_light.svg)
Teilaufgabe a zeigt auch, dass 
gilt, was zusammen mit 
heißt, dass und Eckpunkte eines Quadrats sein können. Der Eckpunkt hat dann die Koordinaten 
![Formula: \begin{array}[t]{rll} \overrightarrow{BC} \times \overrightarrow{BT}&=&\pmatrix{0\\-120\\50} \\[5pt] &=&-10 \cdot\pmatrix{0\\-12\\5} \end{array}](https://www.schullv.de/resources/formulas/fba840e18e3a780ec1ee92b5f4213a9a961fa8f4357bf5d938913a22de2273d9_dark.svg)
Dieser Normalenvektor ergibt die allgemeine Ebenengleichung 
Da der Koordinatenursprung in liegt, folgt direkt 
und es ergibt sich:
![Formula: \begin{array}[t]{rll} \tan \varphi&=&\dfrac{\tfrac{1}{2} \cdot\vert\overline{ST}\vert}{\tfrac{1}{2} \cdot\vert\overline{AB}\vert} \\[5pt] \tan \varphi &=&\dfrac{12}{5} \\[5pt] \varphi &=& \tan^{-1}\left(\dfrac{12}{5}\right) \\[5pt] \varphi &\approx& 67,4^\circ \end{array}](https://www.schullv.de/resources/formulas/9c67dab7929552d20e9caca4f0cb1c83f9de392b69d7faf43f2786c4cb855ebf_light.svg)
![Formula: \begin{array}[t]{rll} \tan \varphi&=&\dfrac{\tfrac{1}{2} \cdot\vert\overline{ST}\vert}{\tfrac{1}{2} \cdot\vert\overline{AB}\vert} \\[5pt] \tan \varphi &=&\dfrac{12}{5} \\[5pt] \varphi &=& \tan^{-1}\left(\dfrac{12}{5}\right) \\[5pt] \varphi &\approx& 67,4^\circ \end{array}](https://www.schullv.de/resources/formulas/9c67dab7929552d20e9caca4f0cb1c83f9de392b69d7faf43f2786c4cb855ebf_dark.svg)
![Formula: \begin{array}[t]{rll} k \cdot 0-5 z&=&5 k-60 &\quad\mid\;:(-5)\\[5pt] z &=&12- k \end{array}](https://www.schullv.de/resources/formulas/d5022d7a71ff4c656fed14c1f9810dcb6584f96b43db8e89db4e544a0a9a9002_light.svg)
![Formula: \begin{array}[t]{rll} k \cdot 0-5 z&=&5 k-60 &\quad\mid\;:(-5)\\[5pt] z &=&12- k \end{array}](https://www.schullv.de/resources/formulas/d5022d7a71ff4c656fed14c1f9810dcb6584f96b43db8e89db4e544a0a9a9002_dark.svg)
schneidet die -Achse somit im Punkt 
Aufgrund der Lage von ergibt sich damit 
Da sich durch Spiegelung an der 
-Ebene aus ergibt, ist 
ein Normalenvektor von Damit folgt:
![Formula: \begin{array}[t]{rll} \pmatrix{0\\k\\-5}\circ\pmatrix{0\\-12\\-5}&=&0 \\[5pt] -12k+25&=&0 &\quad\mid\;-25\\[5pt] -12k&=&-25 &\quad\mid\;:(-12) \\[5pt] k &=&\dfrac{25}{12} \end{array}](https://www.schullv.de/resources/formulas/0805c2b6e54d136118bee65c3a816c1824ba47d29f585c2b8b155b249114258a_light.svg)
![Formula: \begin{array}[t]{rll} \pmatrix{0\\k\\-5}\circ\pmatrix{0\\-12\\-5}&=&0 \\[5pt] -12k+25&=&0 &\quad\mid\;-25\\[5pt] -12k&=&-25 &\quad\mid\;:(-12) \\[5pt] k &=&\dfrac{25}{12} \end{array}](https://www.schullv.de/resources/formulas/0805c2b6e54d136118bee65c3a816c1824ba47d29f585c2b8b155b249114258a_dark.svg)
