Wahlteil

Aufgabe A5 (Analysis)

Gegeben sind die in $Formula: \mathbb{R}$ $Formula: \mathbb{R}$ definierten Funktionen Formula: f und Formula: g. Der Graph von ist symmetrisch bezüglich der Formula: y -Achse, der Graph von ist symmetrisch bezüglich des Koordinatenursprungs. Beide Graphen haben einen Hochpunkt im Punkt $Formula: (2\mid1).$ $Formula: (2\mid1).$

Gib für die Graphen von Formula: f und Formula: g jeweils die Koordinaten und die Art eines weiteren Extrempunkts an.

2 BE

Untersuche die in $Formula: \mathbb{R}$ $Formula: \mathbb{R}$ definierte Funktion Formula: h mit $Formula: h(x) = f(x) \cdot (g(x))^3$ $Formula: h(x) = f(x) \cdot (g(x))^3$ im Hinblick auf eine mögliche Symmetrie ihres Graphen.

3 BE

5 BE

Aufgabe A6 (Analysis)

Der Graph der in $Formula: \mathbb{R}$ $Formula: \mathbb{R}$ definierten Funktion $Formula: f : x \mapsto \tfrac{1}{4}x^2$ $Formula: f : x \mapsto \tfrac{1}{4}x^2$ und die Gerade mit der Gleichung Formula: y = 1 schließen ein Flächenstück ein (vgl. Abbildung). Durch Rotation dieses Flächenstücks um die -Achse wird ein Körper erzeugt. Bestimme das Volumen dieses Körpers.

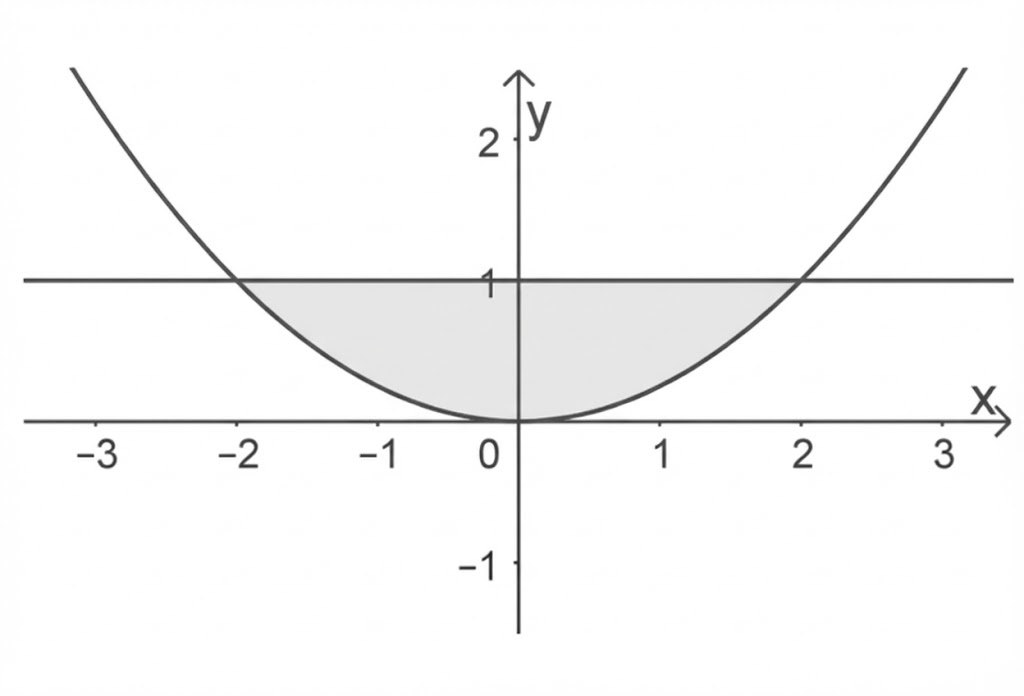
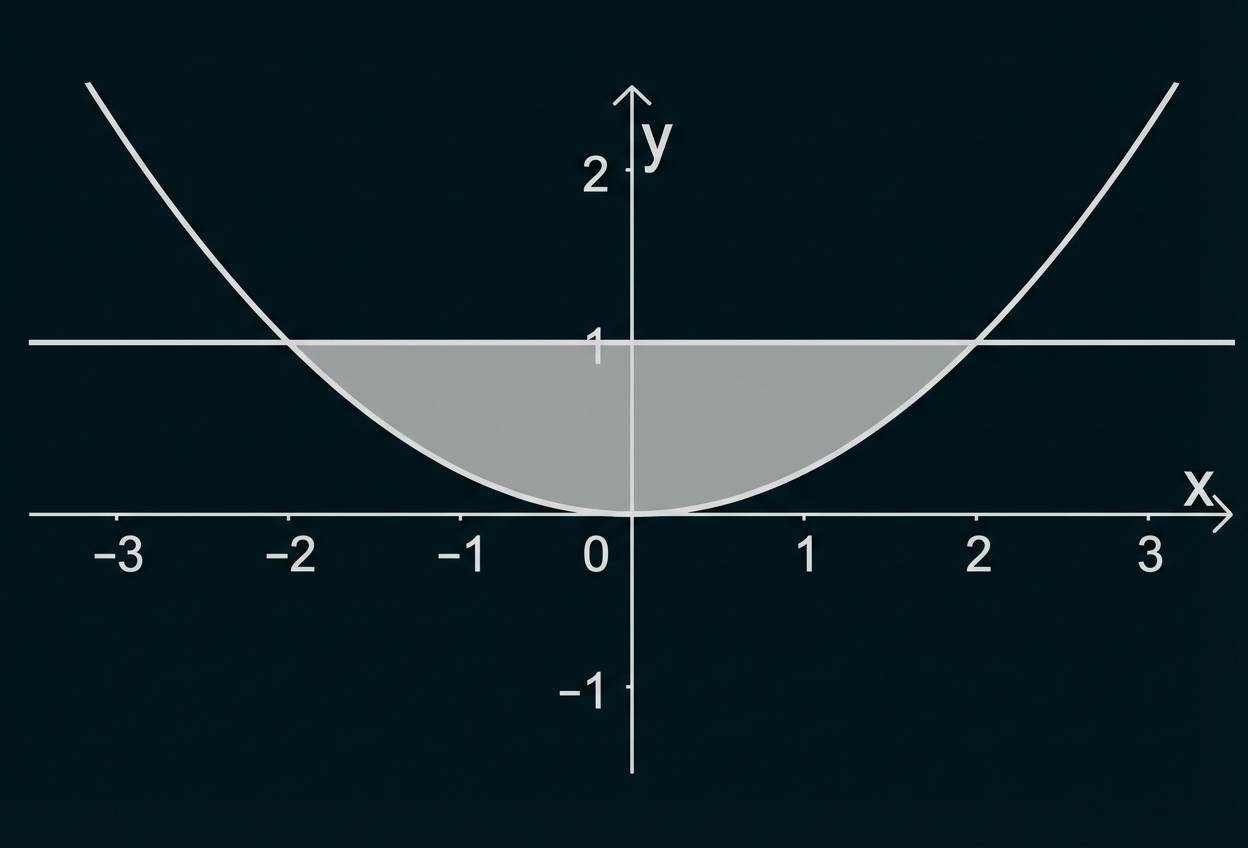
Koordinatensystem mit Parabel y = x², horizontaler Linie y = 1 und schattierter Fläche zwischen Parabel und Linie.

5 BE

Aufgabe A7 (Stochastik)

Bei einem Spiel werfen zwei Spieler abwechselnd jeweils drei Würfel. Das Spiel endet, wenn ein Spieler die Augensumme Formula: 18 erzielt oder die Augensumme des vorausgegangenen Wurfs des anderen Spielers nicht übertrifft.

Beim ersten Wurf des Spiels erzielt ein Spieler die Augensumme Formula: 15.

Berechne die Wahrscheinlichkeit dafür, dass dieser Spieler die Würfel im selben Spiel noch einmal wirft. Erläutere dein Vorgehen.

5 BE

Aufgabe A8 (Stochastik)

Eine Gärtnerei, die Tulpen in den Farben Gelb, Orange und Rot züchtet, stellt Sträuße mit jeweils Formula: 15 Tulpen zusammen.

Einer der Sträuße soll Tulpen in zwei verschiedenen Farben enthalten. Die Anzahl der Möglichkeiten, diesen Strauß zusammenzustellen, kann mit dem Term $Formula: \tbinom{3}{2} \cdot 14$ $Formula: \tbinom{3}{2} \cdot 14$ berechnet werden. Beschreibe für jeden der beiden Faktoren die Bedeutung im Sachzusammenhang.

2 BE

In einem der Sträuße sollen zu jeder der drei Farben mindestens vier und höchstens sechs Tulpen enthalten sein. Bestimme die Anzahl der Möglichkeiten, diesen Strauß zusammenzustellen.

3 BE

5 BE

Aufgabe A9 (Geometrie)

Gegeben sind die Punkte $Formula: A(0\mid0\mid0), B(3\mid4\mid1),$ $Formula: A(0\mid0\mid0), B(3\mid4\mid1),$ $Formula: C(1\mid7\mid3)$ $Formula: C(1\mid7\mid3)$ und $D(-2\mid3\mid2).$

Weise nach, dass das Viereck Formula: ABCD ein Parallelogramm ist.

1 BE

Der Punkt Formula: T liegt auf der Strecke $Formula: \overline{AC}.$ $Formula: \overline{AC}.$ Das Dreieck Formula: ABT hat bei Formula: B einen rechten Winkel. Ermittle das Verhältnis der Länge der Strecke $Formula: \overline{AT}$ $Formula: \overline{AT}$ zur Länge der Strecke $Formula: \overline{CT}.$ $Formula: \overline{CT}.$

4 BE

5 BE

Aufgabe A10 (Geometrie)

Die Punkte Formula: P und Formula: Q liegen in der Ebene Formula: E : 5x_1 − 4x_2 + 3x_3 − 6 = 0 und haben voneinander den Abstand Formula: 10. Ermittle mögliche Koordinaten von und Formula: Q.

5 BE

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung A5 (Analysis)

Der Graph von Formula: f hat den Hochpunkt $Formula: (-2 \mid 1),$ $Formula: (-2 \mid 1),$ der Graph von Formula: g den Tiefpunkt $Formula: (-2 \mid-1).$ $Formula: (-2 \mid-1).$

$Formula: \begin{array}[t]{rll} h(-x)&=& f(-x) \cdot(g(-x))^3 \\[5pt] &=& f(x) \cdot(-g(x))^3 \\[5pt] &=& -f(x) \cdot(g(x))^3 \\[5pt] &=& -h(x) \end{array}$ $Formula: \begin{array}[t]{rll} h(-x)&=& f(-x) \cdot(g(-x))^3 \\[5pt] &=& f(x) \cdot(-g(x))^3 \\[5pt] &=& -f(x) \cdot(g(x))^3 \\[5pt] &=& -h(x) \end{array}$

Damit ist der Graph von Formula: h symmetrisch bezüglich des Koordinatenursprungs.

Lösung A6 (Analysis)

Für $Formula: x \geq 0$ $Formula: x \geq 0$ gilt:

$Formula: \begin{array}[t]{rll} x&=& \dfrac{1}{4} y^2 &\quad\mid\;\cdot4 \\[5pt] 4x &=& y^2 &\quad\mid\;\sqrt{\;}\\[5pt] \sqrt{4x} &=& y \end{array}$ $Formula: \begin{array}[t]{rll} x&=& \dfrac{1}{4} y^2 &\quad\mid\;\cdot4 \\[5pt] 4x &=& y^2 &\quad\mid\;\sqrt{\;}\\[5pt] \sqrt{4x} &=& y \end{array}$

Gesuchtes Volumen:

$Formula: \begin{array}[t]{rll} V&=& \pi \cdot \displaystyle\int_0^1\left(\sqrt{4 x}\right)^2 \;\mathrm d x \\[5pt] &=& \pi \cdot \displaystyle\int_0^1 4 x \;\mathrm d x \\[5pt] &=& \pi \cdot\left[2 x^2\right]_0^1\\[5pt] &=& 2\pi \end{array}$ $Formula: \begin{array}[t]{rll} V&=& \pi \cdot \displaystyle\int_0^1\left(\sqrt{4 x}\right)^2 \;\mathrm d x \\[5pt] &=& \pi \cdot \displaystyle\int_0^1 4 x \;\mathrm d x \\[5pt] &=& \pi \cdot\left[2 x^2\right]_0^1\\[5pt] &=& 2\pi \end{array}$

Lösung A7 (Stochastik)

Der Spieler wird noch einmal würfeln, wenn der andere Spieler beim nächsten Wurf die Augensumme Formula: 16 oder die Augensumme Formula: 17 erzielt.

Für den Wurf des anderen Spielers kommen also folgende Fälle infrage:

für die Augensumme einmal und zweimal zweimal und einmal
für die Augensumme einmal und zweimal

Die Wahrscheinlichkeit dafür, dass der Spieler noch einmal würfelt, beträgt demnach $Formula: 2 \cdot 3 \cdot \tfrac{1}{6^3}+3 \cdot \tfrac{1}{6^3}$ $Formula: 2 \cdot 3 \cdot \tfrac{1}{6^3}+3 \cdot \tfrac{1}{6^3}$ $Formula: =\tfrac{9}{216}=\tfrac{1}{24}.$ $Formula: =\tfrac{9}{216}=\tfrac{1}{24}.$

Lösung A8 (Stochastik)

Der erste Faktor gibt die Anzahl der Möglichkeiten an, zwei der drei Farben auszuwählen, der zweite die Anzahl der Möglichkeiten für die Anzahl der Tulpen einer der beiden Farben.

Es gibt eine Möglichkeit, den Strauß aus jeweils fünf Tulpen der drei Farben, und $Formula: 3 \cdot 2$ $Formula: 3 \cdot 2$ Möglichkeiten, den Strauß aus vier Tulpen einer ersten Farbe, fünf Tulpen einer zweiten Farbe und sechs Tulpen der dritten Farbe zusammenzustellen — insgesamt also sieben Möglichkeiten.

Lösung A9 (Geometrie)

$Formula: \overrightarrow{AB}=\pmatrix{3 \\ 4 \\ 1}=\overrightarrow{DC}$ $Formula: \overrightarrow{AB}=\pmatrix{3 \\ 4 \\ 1}=\overrightarrow{DC}$

Formula: T hat den Ortsvektor $Formula: \lambda \cdot \overrightarrow{AC}.$ $Formula: \lambda \cdot \overrightarrow{AC}.$

$Formula: \begin{array}[t]{rll} \overrightarrow{AB} \circ \overrightarrow{TB}&=& 0 \\[5pt] \pmatrix{3 \\ 4 \\ 1} \circ \pmatrix{3-\lambda \\ 4-7 \lambda \\ 1-3 \lambda} &=& 0 \\[5pt] 26-34 \lambda &=& 0 &\quad\mid\;-26\\[5pt] -34 \lambda &=& -26 &\quad\mid\;:(-34)\\[5pt] \lambda &=& \dfrac{13}{17} \end{array}$ $Formula: \begin{array}[t]{rll} \overrightarrow{AB} \circ \overrightarrow{TB}&=& 0 \\[5pt] \pmatrix{3 \\ 4 \\ 1} \circ \pmatrix{3-\lambda \\ 4-7 \lambda \\ 1-3 \lambda} &=& 0 \\[5pt] 26-34 \lambda &=& 0 &\quad\mid\;-26\\[5pt] -34 \lambda &=& -26 &\quad\mid\;:(-34)\\[5pt] \lambda &=& \dfrac{13}{17} \end{array}$

Damit beträgt das gesuchte Verhältnis Formula: 13: 4.

Lösung A10 (Geometrie)

Formula: P kann als Punkt der Formula: x_3 -Ebene gewählt werden. Einsetzen der allgemeinen Koordinaten in die Ebenengleichung von Formula: E liefert dann $Formula: P(0\mid0\mid2).$ $Formula: P(0\mid0\mid2).$

Der Vektor $Formula: \overrightarrow{v}=\left(\begin{array}{c}5 \\ -4 \\ 3\end{array}\right) \times\left(\begin{array}{l}1 \\ 0 \\ 0\end{array}\right)=\left(\begin{array}{l}0 \\ 3 \\ 4\end{array}\right)$ $Formula: \overrightarrow{v}=\left(\begin{array}{c}5 \\ -4 \\ 3\end{array}\right) \times\left(\begin{array}{l}1 \\ 0 \\ 0\end{array}\right)=\left(\begin{array}{l}0 \\ 3 \\ 4\end{array}\right)$ ist orthogonal zum Normalenvektor von Formula: E, verläuft also parallel zu Formula: E. Damit folgen für mögliche Koordinaten von Formula: Q:

$Formula: \begin{array}[t]{rll} \overrightarrow{OQ}&=& \overrightarrow{OP}+\dfrac{10}{\lvert\overrightarrow{v}\rvert} \cdot \overrightarrow{v} \\[5pt] &=& \pmatrix{0 \\ 0 \\ 2} + \dfrac{10}{5}\cdot\pmatrix{0 \\ 3 \\ 4} \\[5pt] &=& \pmatrix{0 \\ 6 \\ 10} \end{array}$ $Formula: \begin{array}[t]{rll} \overrightarrow{OQ}&=& \overrightarrow{OP}+\dfrac{10}{\lvert\overrightarrow{v}\rvert} \cdot \overrightarrow{v} \\[5pt] &=& \pmatrix{0 \\ 0 \\ 2} + \dfrac{10}{5}\cdot\pmatrix{0 \\ 3 \\ 4} \\[5pt] &=& \pmatrix{0 \\ 6 \\ 10} \end{array}$

Somit folgt $Formula: P(0\mid0\mid 2)$ $Formula: P(0\mid0\mid 2)$ und $Formula: Q(0\mid6\mid 10).$ $Formula: Q(0\mid6\mid 10).$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?