Teil B

Betrachtet werden die Punkte $A(2\mid0\mid 0), B(-2\mid0\mid 0),$ $C(-2\mid0\mid 3), D(2\mid0\mid 3),$ $S(0\mid-5\mid 0), E_k(0\mid k\mid 0)$ und $F_k(0\mid k\mid 30-3 k)$ mit $0\lt k \leq 10.$
Die Abbildung zeigt einen zusammengesetzten Körper, der aus der Pyramide $ABCDS$ und einem Körper $ABCDE_k F_k$ besteht.

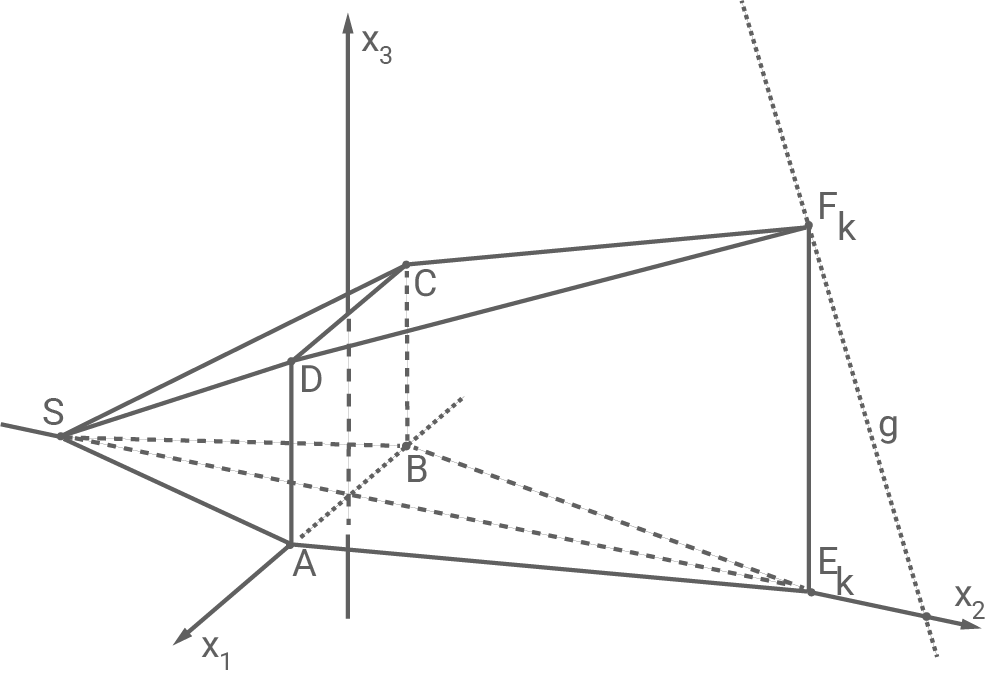
Diagramm mit Achsen und Linien, das geometrische Beziehungen darstellt.

Das Viereck $ABCD$ ist ein Rechteck. Untersuche, ob $ABCD$ auch ein Quadrat ist. Berechne das Volumen der Pyramide $ABCDS.$

(4 BE)

Jeder Punkt $F_k$ liegt auf der Geraden $g$ (vgl. Abbildung).

Gib den Ortsvektor eines Punktes auf $g$ an und zeige, dass $\pmatrix{0\\1\\-3}$ ein Richtungsvektor von $g$ ist.

(2 BE)

Begründe, dass die $x_1x_3$ -Ebene für keinen Wert von $k$ eine Symmetrieebene des zusammengesetzten Körpers ist.

(3 BE)

Die Punkte $C, D$ und $S$ liegen in der Ebene $L.$ Bestimme eine Gleichung von $L$ in Koordinatenform. Ermittle den Wert von $k,$ für den der Eckpunkt $F_k$ ebenfalls in $L$ liegt.

(5 BE)

Im Dreieck $D F_k C$ wird der Innenwinkel im Punkt $F_k$ betrachtet. Ermittle denjenigen Wert von $k,$ für den die Größe dieses Winkels maximal ist, und erläutere deinen Lösungsweg.

(6 BE)

(20 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$\boldsymbol{ABCD}$ untersuchen

Für zwei der Seitenlängen gilt:

$\begin{array}[t]{rlll} \left\vert\overrightarrow{AB}\right\vert&=&\left\vert\pmatrix{-2-2\\0-0\\0-0}\right\vert \\[5pt] &=&4 \end{array}$

$\begin{array}[t]{rlll} \left\vert\overrightarrow{BC}\right\vert&=&\left\vert\pmatrix{-2-(-2)\\0-0\\3-0}\right\vert \\[5pt] &=&3 \end{array}$

Da die Seiten von $ABCD$ unterschiedlich lang sind, handelt es sich nicht um ein Quadrat.

Volumen berechnen

Aus den Koordinaten der Punkte wird deutlich, dass die Höhe der Pyramide $5\;\text{LE}$ beträgt. Zusammen mit den oben berechneten Seitenlängen der Grundfläche folgt für das Volumen $V:$

$V=\dfrac{1}{3}\cdot3\cdot4\cdot5=20\;[\text{VE}]$

Ortsvektor angeben

Für $k=1$ folgt $F_1(0\mid1\mid27).$ Ein möglicher Ortsvektor ist somit gegeben durch:

$\overrightarrow{OF_1}=\pmatrix{0\\1\\27}$

Richtungsvektor zeigen

Ein möglicher Richtungsvektor ergibt sich als:

$\begin{array}[t]{rlll} \overrightarrow{F_1F_2}&=&\pmatrix{0\\2\\24}-\pmatrix{0\\1\\27} \\[5pt] &=&\pmatrix{0\\1\\-3} \end{array}$

Damit die $x_1x_3$ -Ebene eine Symmetrieebene des Körpers ist, müssen $E_k$ und $F_k$ im Punkt $(0\mid5\mid0)$ zusammenfallen. Der Punkt $E_k$ besitzt diese Koordinaten für $k=5.$ Einsetzen in die Koordinaten von $F_k$ liefert allerdings $F_k(0\mid5\mid15).$ Somit ist die $x_1x_3$ -Ebene für keinen Wert von $k$ eine Symmetrieebene des Körpers.

Gleichung bestimmen

Zwei Spannvektoren von $L$ ergeben sich wie folgt:

$\begin{array}[t]{rlll} \overrightarrow{CD}&=&\pmatrix{2-(-2)\\0-0\\3-3} \\[5pt] &=&\pmatrix{4\\0\\0} \end{array}$

$\begin{array}[t]{rlll} \overrightarrow{CS}&=&\pmatrix{0-(-2)\\-5-0\\0-3} \\[5pt] &=&\pmatrix{2\\-5\\-3} \end{array}$

Mit Hilfe des CAS folgt für das Kreuzprodukt dieser beiden Vektoren:

$\overrightarrow{CD}\times\overrightarrow{CS}=\pmatrix{0\\12\\-20}$

Mit diesem Vektor als Normalenvektor ergibt sich $L:12x_2-20x_3=d.$ Einsetzen der Koordinaten von z.B. $S$ liefert:

$\begin{array}[t]{rlll} 12\cdot(-5)-20\cdot0&=&d \\[5pt] -60&=&d \end{array}$

Eine mögliche Gleichung von $L$ in Koordinatenform ist somit durch $L:12x_2-20x_3=-60$ gegeben.

Wert von $\boldsymbol{k}$ ermitteln

Einsetzen der Koordinaten von $F_k$ in die Ebenengleichung von $L$ und auflösen nach $k$ mit dem solve-Befehl des CAS liefert:

$k=\dfrac{15}{2}$

Wert ermitteln

$\pmatrix{0\\k\\27-3k}\cdot\pmatrix{0\\1\\-3}=0$

Auflösen dieser Gleichung nach $k$ mit dem CAS liefert für die gesuchte Lösung $k=8,1.$

Lösungsweg erläutern

Das Dreieck $DF_kC$ ist gleichschenklig bezüglich der Grundseite $\overline{CD}.$ Der Mittelpunkt $M$ der Strecke besitzt die Koordinaten $M(0\mid0\mid3).$ Je kleiner die Höhe $\left\vert\overline{MF}_{k}\right\vert$ ist, desto größer ist der Winkel im Punk $F_k.$ Diese Höhe wird minimal, wenn der Vektor $\overrightarrow{MF_{k}}$ senkrecht zum Richtungsvektor der Gerade $g$ steht, d.h. das obige Skalarprodukt Null ergibt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?