B1 – Analysis

Gegeben ist die in $Formula: \mathbb{R}$ $Formula: \mathbb{R}$ definierte Funktion Formula: f mit $Formula: f(x)=\tfrac{1}{2} \cdot \mathrm e^{-(x-5)}+\tfrac{1}{2}.$ $Formula: f(x)=\tfrac{1}{2} \cdot \mathrm e^{-(x-5)}+\tfrac{1}{2}.$ Ihr Graph wird mit Formula: G_f bezeichnet.

Beschreibe, wie Formula: G_f aus dem Graphen der in $Formula: \mathbb{R}$ $Formula: \mathbb{R}$ definierten Funktion $Formula: x \mapsto \mathrm e^{-x}$ $Formula: x \mapsto \mathrm e^{-x}$ hervorgeht, und gib die Wertemenge von Formula: f an.

4 BE

Die Funktion Formula: f ist umkehrbar. Zeige, dass die Funktion $Formula: u: x\mapsto 5-\ln (2 x-1)$ $Formula: u: x\mapsto 5-\ln (2 x-1)$ mit geeignet gewählter Definitionsmenge Formula: D_u die Umkehrfunktion von ist. Gib an.

2 BE

Gib alle Stammfunktionen von Formula: f an und zeige, dass jede dieser Stammfunktionen die Wertemenge $Formula: \mathbb{R}$ $Formula: \mathbb{R}$ besitzt.

3 BE

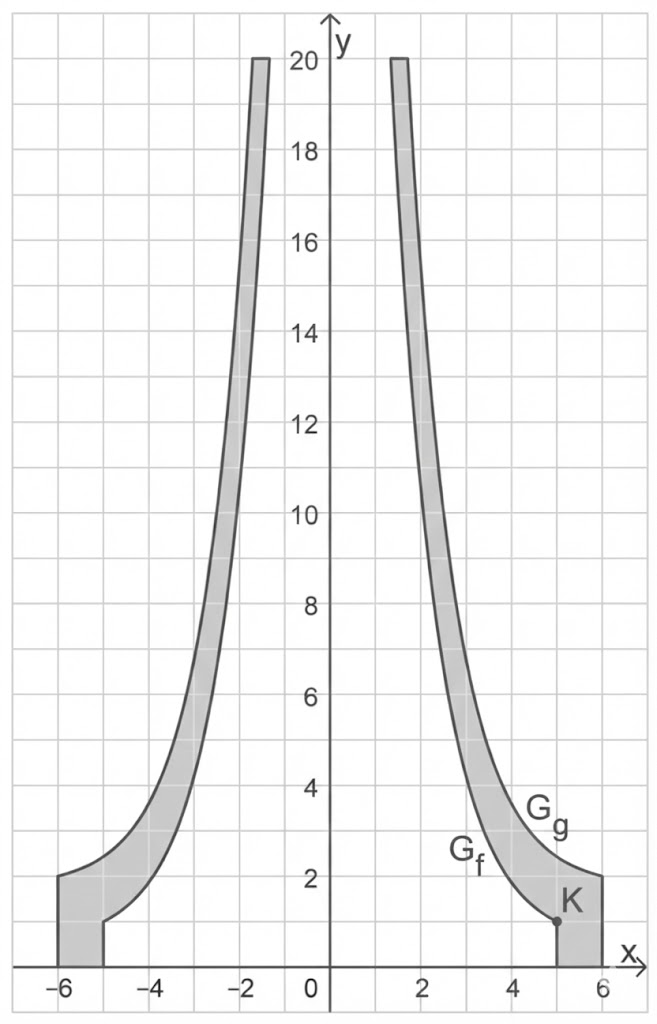
Ein $Formula: 20\;\text{m}$ $Formula: 20\;\text{m}$ hoher Kühlturm soll gesprengt werden. Abbildung 1 zeigt schematisch einen Längsschnitt des Kühlturms. Der Turm ist rotationssymmetrisch; die Rotationsachse entspricht der Formula: y -Achse im eingezeichneten Koordinatensystem. Der Turmboden als Teil dieses Längsschnitts liegt auf der Formula: x -Achse. Eine Längeneinheit entspricht $Formula: 1\;\text{m}$ $Formula: 1\;\text{m}$ in der Wirklichkeit.

Die Profillinie des Längsschnitts der inneren Wandfläche wird im ersten Quadranten für $Formula: x \leq 5$ $Formula: x \leq 5$ und $Formula: y \leq 20$ $Formula: y \leq 20$ modellhaft durch den Graphen der Funktion Formula: f beschrieben. Analog beschreibt für $Formula: x \leq 6$ $Formula: x \leq 6$ und $Formula: y \leq 20$ $Formula: y \leq 20$ der Graph Formula: G_g einer Funktion im ersten Quadranten die Profillinie des Längsschnitts der äußeren Wandfläche.

Der untere Teil des Turms ist ein Sockelring, dessen Wandflächen Zylindermäntel mit den Radien $Formula: 5\;\text{m}$ $Formula: 5\;\text{m}$ bzw. $Formula: 6\;\text{m}$ $Formula: 6\;\text{m}$ und den Höhen $Formula: 1\;\text{m}$ $Formula: 1\;\text{m}$ bzw. $Formula: 2\;\text{m}$ $Formula: 2\;\text{m}$ sind. Im Modell besitzt die innere Profillinie im Punkt Formula: K dadurch einen Knick.

Der Innenradius des kreisringförmigen oberen Turmrands in Metern wird mit Formula: r bezeichnet.

Koordinatensystem mit zwei schattierten, symmetrischen Kurvenbereichen; rechts die Punkte G_f, G_g und K.

Berechne Formula: r auf eine Dezimale genau.

(zur Kontrolle: $Formula: \small{r \approx 1,3}$ $Formula: \small{r \approx 1,3}$ )

2 BE

Berechne die Größe des Winkels, der von dem gekrümmten und dem vertikal verlaufenden Teil der inneren Profillinie im Punkt Formula: K eingeschlossen wird.

3 BE

Zum Anbringen einer Sprengladung wird eine Bohrung in die Wand geplant. Der Bohrkanal wird im Modell durch eine Strecke beschrieben, die im Punkt Formula: K beginnt und einen Steigungswinkel von $Formula: 60^{\circ}$ $Formula: 60^{\circ}$ hat.

Begründe, dass dabei der senkrechte Teil der äußeren Wandfläche nicht durchbohrt werden kann.

3 BE

Die Bohrung soll die Wand vollständig durchdringen. Beschreibe, wie bei der Berechnung der dazu erforderlichen Länge des Bohrkanals schrittweise vorgegangen werden könnte.

4 BE

An der Position, die im Modell dem Punkt $Formula: (5 \mid 0)$ $Formula: (5 \mid 0)$ entspricht, befindet sich ein Scheinwerfer. Die höchste Stelle an der Innenfläche der Turmwand, die durch den Scheinwerfer gerade noch beleuchtet wird, befindet sich gegenüber dem Scheinwerfer. Berechne die Höhe dieser Stelle.

5 BE

Berechne das Volumen des Hohlraums im Turminneren vom Turmboden bis zur Höhe $Formula: 20\;\text{m}.$ $Formula: 20\;\text{m}.$

4 BE

30 BE

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Formula: G_f geht aus dem Graphen der Funktion $Formula: x \mapsto \mathrm{e}^{-x}$ $Formula: x \mapsto \mathrm{e}^{-x}$ hervor durch:

Verschiebung um in positive -Richtung
Streckung in -Richtung mit dem Faktor $Formula: \tfrac{1}{2}$ $Formula: \tfrac{1}{2}$
Verschiebung um $Formula: \tfrac{1}{2}$ $Formula: \tfrac{1}{2}$ in positive -Richtung

Die Wertemenge ist gegeben durch $Formula: \left] \tfrac{1}{2} ;+\infty\right[.$ $Formula: \left] \tfrac{1}{2} ;+\infty\right[.$

$Formula: \begin{array}[t]{rll} u(f(x))&=&5-\ln \left(2\cdot\left(\dfrac{1}{2} \cdot \mathrm e^{-(x-5)}+\dfrac{1}{2}\right)-1\right) \\[5pt] &=&5+(x-5) \\[5pt]&=&x \end{array}$ $Formula: \begin{array}[t]{rll} u(f(x))&=&5-\ln \left(2\cdot\left(\dfrac{1}{2} \cdot \mathrm e^{-(x-5)}+\dfrac{1}{2}\right)-1\right) \\[5pt] &=&5+(x-5) \\[5pt]&=&x \end{array}$

Damit ist Formula: u eine Umkehrfunktion von Formula: f. Die passende Definitionsmenge ist gegeben durch die Wertemenge von Formula: f, also gilt $Formula: D_u=\left] \tfrac{1}{2} ;+\infty\right[.$ $Formula: D_u=\left] \tfrac{1}{2} ;+\infty\right[.$

Die Stammfunktionen von Formula: f sind genau die in $Formula: \mathbb{R}$ $Formula: \mathbb{R}$ definierten Funktionen $Formula: F_c: x \mapsto \tfrac{1}{2} x-\tfrac{1}{2} \mathrm{e}^{5-x}+c$ $Formula: F_c: x \mapsto \tfrac{1}{2} x-\tfrac{1}{2} \mathrm{e}^{5-x}+c$ mit $Formula: \mathrm{c} \in \mathbb{R}.$ $Formula: \mathrm{c} \in \mathbb{R}.$ Wegen $Formula: \lim\limits_{x\to+\infty}F_c(x)=+\infty$ $Formula: \lim\limits_{x\to+\infty}F_c(x)=+\infty$ und $Formula: \lim\limits_{x\to-\infty}F_c(x)=-\infty$ $Formula: \lim\limits_{x\to-\infty}F_c(x)=-\infty$ besitzt jede Stammfunktion die Wertemenge $Formula: \mathbb{R}.$ $Formula: \mathbb{R}.$

Auflösen von Formula: f(r)=20 nach Formula: r mit dem MMS liefert auf eine Dezimalstelle gerundet $Formula: r\approx1,3.$ $Formula: r\approx1,3.$

Für die gesuchte Winkelgröße $Formula: \alpha$ $Formula: \alpha$ gilt:

$Formula: \tan \left(\alpha-90^{\circ}\right)=\left\vert f'(5)\right\vert$ $Formula: \tan \left(\alpha-90^{\circ}\right)=\left\vert f'(5)\right\vert$

Auflösen nach $Formula: \alpha$ $Formula: \alpha$ mit dem MMS liefert $Formula: \alpha \approx 116,6^{\circ}.$ $Formula: \alpha \approx 116,6^{\circ}.$

Der höchste Punkt des senkrechten Teils der äußeren Profillinie hat die Koordinaten $Formula: P(6 \mid 2).$ $Formula: P(6 \mid 2).$ Da die Strecke $Formula: \overline{KP}$ $Formula: \overline{KP}$ eine Steigung von Formula: 1 besitzt, ist die Größe des Winkels zwischen $Formula: \overline{KP}$ $Formula: \overline{KP}$ und der Horizontalen $Formula: 45^{\circ}$ $Formula: 45^{\circ}$ und damit kleiner als $Formula: 60^{\circ}.$ $Formula: 60^{\circ}.$

Der Verlauf der Bohrung wird im Modell durch eine Gerade Formula: b mit der Gleichung Formula: y=mx+t beschrieben. Dabei ist $Formula: m=\tan \left(60^{\circ}\right);$ $Formula: m=\tan \left(60^{\circ}\right);$ zudem liegt der Punkt Formula: K auf Formula: b. Der Punkt Formula: S ist der Schnittpunkt von mit dem Graphen von Formula: g. Die Länge der Strecke $Formula: \overline{KS}$ $Formula: \overline{KS}$ ist die gesuchte Länge des Bohrkanals in Metern.

Die Steigung des Graphen Formula: G_f bei Formula: x=a beträgt $Formula: -\tfrac{1}{2} \cdot \mathrm e^{5-a}.$ $Formula: -\tfrac{1}{2} \cdot \mathrm e^{5-a}.$ Einsetzen der Koordinaten eines allgemeinen Punktes $Formula: (a\mid f(a))$ $Formula: (a\mid f(a))$ in die allgemeine Tangentengleichung liefert somit, dass die Tangente an Formula: G_f an der Stelle Formula: x=a der Graph einer linearen Funktion Formula: s mit $Formula: s(x)=-\tfrac{1}{2}\cdot\mathrm e^{5-a} x$ $Formula: s(x)=-\tfrac{1}{2}\cdot\mathrm e^{5-a} x$ $Formula: +\tfrac{1}{2}\cdot\left(1+(a+1) \cdot \mathrm e^{5-a}\right)$ $Formula: +\tfrac{1}{2}\cdot\left(1+(a+1) \cdot \mathrm e^{5-a}\right)$ ist. Einsetzen von Formula: x=5 und auflösen nach Formula: a liefert mit dem MMS:

$Formula: a\approx3,72$ $Formula: a\approx3,72$

Die Formula: x -Koordinate des Schnittpunkts Formula: L dieser Tangente mit dem Graphen, der aus Formula: G_f durch Spiegelung an der Formula: y -Achse hervorgeht erfüllt Formula: s(x_L)=f(-x_L). Auflösen nach Formula: x_L mit dem MMS liefert:

$Formula: x_L\approx-1,84$ $Formula: x_L\approx-1,84$

Einsetzen in die Funktionsgleichung des gespiegelten Graphs von Formula: f liefert mit dem MMS $Formula: f\left(-x_L\right) \approx 12,3.$ $Formula: f\left(-x_L\right) \approx 12,3.$ Die Höhe der gesuchten Stelle beträgt somit ca. $Formula: 12,3\;\text{m}.$ $Formula: 12,3\;\text{m}.$

Unter Verwendung der Umkehrfunktion Formula: u von Formula: f aus Aufgabe c ergibt sich mit dem MMS:

$Formula: 5^2 \cdot \pi \cdot 1+\pi \cdot \displaystyle\int_1^{20}(u(x))^2 \;\mathrm d x\approx416,1$ $Formula: 5^2 \cdot \pi \cdot 1+\pi \cdot \displaystyle\int_1^{20}(u(x))^2 \;\mathrm d x\approx416,1$

Das gesuchtes Volumen beträgt somit ca. $Formula: 416\;\mathrm{m}^3.$ $Formula: 416\;\mathrm{m}^3.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?