Aufgabe 3A
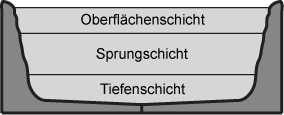
Stehende Gewässer weisen eine Schichtung des Wassers auf. Modellhaft werden drei Schichten unterschieden: die kalte Tiefenschicht, die warme Oberflächenschicht und die dazwischenliegende Sprungschicht, in der die Temperatur mit der Tiefe sinkt.
Durch unterschiedliche Vorgänge kommt es zu einem gewissen Austausch zwischen den Schichten, sodass sich die Schichtdicken verändern. Die nebenstehende Tabelle beschreibt die Übergänge zwischen den Schichten pro Zeiteinheit. Für diese Modellierung wird vorausgesetzt, dass sich diese Entwicklung in der beschriebenen Weise fortsetzen wird.
| von | ||||
| O | S | T | ||
|---|---|---|---|---|
| O | 0,9 | 0,1 | 0 | |
| nach | S | 0,1 | 0,85 | 0,1 |
| T | 0 | 0,05 | 0,9 |
a) Stellen Sie die Daten aus der Übergangstabelle in einem Übergangsgraphen dar.
Erläutern Sie die Werte der mittleren Zeile der Tabelle im Sachzusammenhang.
Bestimmen Sie die Schichtdicken nach fünf Zeiteinheiten auf Zentimeter genau, wenn zu Beginn jede der Schichten 3 m dick ist.
Erläutern Sie die Werte der mittleren Zeile der Tabelle im Sachzusammenhang.
Bestimmen Sie die Schichtdicken nach fünf Zeiteinheiten auf Zentimeter genau, wenn zu Beginn jede der Schichten 3 m dick ist.
(10P)
b) Nach diesem Modell werden die Oberflächen- und die Sprungschicht mit der Zeit gleich dick.
Erstellen Sie begründet eine veränderte Übergangsmatrix so, dass die Sprungschicht auf lange Sicht dicker ist als die Oberflächenschicht.
Erstellen Sie begründet eine veränderte Übergangsmatrix so, dass die Sprungschicht auf lange Sicht dicker ist als die Oberflächenschicht.
(6P)
c) Für eine andere Modellierung eines 9 m tiefen Gewässers wird die Übergangsmatrix
 angegeben.
Geben Sie an, welche Werte
angegeben.
Geben Sie an, welche Werte  annehmen darf.
annehmen darf.
Bestimmen Sie eine Matrix so, dass sich eine stabile Verteilung mit einer 1 m dicken Oberflächen-, einer 3 m dicken Sprung- und einer 5 m dicken Tiefenschicht ergibt.
so, dass sich eine stabile Verteilung mit einer 1 m dicken Oberflächen-, einer 3 m dicken Sprung- und einer 5 m dicken Tiefenschicht ergibt.
Bestimmen Sie eine Matrix
(8P)
(24P)
a)  Übergangsgraph
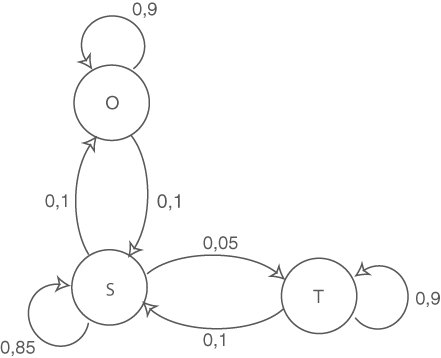
Den Übergangsgraphen erhältst du, indem du jeder Schicht einen Knoten zuordnest. Durch Pfeile zwischen den entsprechenden Knoten, kannst du die Übergange zwischen den Schichten darstellen. Beschrifte die Pfeile jeweils mit der zugehörigen Übergangswahrscheinlichkeit aus der Tabelle.
Übergangsgraph
Den Übergangsgraphen erhältst du, indem du jeder Schicht einen Knoten zuordnest. Durch Pfeile zwischen den entsprechenden Knoten, kannst du die Übergange zwischen den Schichten darstellen. Beschrifte die Pfeile jeweils mit der zugehörigen Übergangswahrscheinlichkeit aus der Tabelle.
Dein Übergangsgraph sollte dann wie folgt aussehen:
 Mittlere Zeile im Sachzusammenhang erklären
Du sollst die Werte der mittleren Zeile im Sachzusammenhang erklären. Die Werte der Zeile geben an, dass pro Zeiteinheit
Mittlere Zeile im Sachzusammenhang erklären
Du sollst die Werte der mittleren Zeile im Sachzusammenhang erklären. Die Werte der Zeile geben an, dass pro Zeiteinheit  von der Dicke der Oberflächenschicht zur Dicke der Sprungschicht hinzukommen,
von der Dicke der Oberflächenschicht zur Dicke der Sprungschicht hinzukommen,  von der Dicke der Sprungschicht erhalten bleiben und
von der Dicke der Sprungschicht erhalten bleiben und  von der Dicke der Tiefenschicht zur Dicke der Sprungschicht hinzukommen.
von der Dicke der Tiefenschicht zur Dicke der Sprungschicht hinzukommen.
 Schichtdicke bestimmen
Zu Beginn ist jede der Schichten 3 m dick, du sollst die Schichtdicken nach fünf Zeiteinheiten berechnen. Die Übergangsmatrix
Schichtdicke bestimmen
Zu Beginn ist jede der Schichten 3 m dick, du sollst die Schichtdicken nach fünf Zeiteinheiten berechnen. Die Übergangsmatrix
 gibt die Übergänge pro Zeiteinheit an, das bedeutet, dass du die Matrix 5 mal mit sich selbst multiplizieren musst, um die Verteilung pro 5 Zeiteinheiten zu erhalten. Jetzt musst du noch die Schichtdicke von je 3 m beachten, diese also mit der Verteilung pro 5 Zeiteinheiten multiplizieren. Du erhältst dann für die Verteilung nach 5 Zeiteinheiten:
gibt die Übergänge pro Zeiteinheit an, das bedeutet, dass du die Matrix 5 mal mit sich selbst multiplizieren musst, um die Verteilung pro 5 Zeiteinheiten zu erhalten. Jetzt musst du noch die Schichtdicke von je 3 m beachten, diese also mit der Verteilung pro 5 Zeiteinheiten multiplizieren. Du erhältst dann für die Verteilung nach 5 Zeiteinheiten:
 Nach fünf Zeiteinheiten beträgt die Dicke der Oberflächenschicht
Nach fünf Zeiteinheiten beträgt die Dicke der Oberflächenschicht  , die der Sprungschicht
, die der Sprungschicht  und die der Tiefenschicht
und die der Tiefenschicht  .
.
Dein Übergangsgraph sollte dann wie folgt aussehen:

b)  Übergangsmatrix erstellen
Erstelle eine veränderte Übergangsmatrix so, dass die Sprungschicht auf lange Sicht dicker ist als die Oberflächenschicht. Eine mögliche Übergangsmatrix ist gegeben durch
Übergangsmatrix erstellen
Erstelle eine veränderte Übergangsmatrix so, dass die Sprungschicht auf lange Sicht dicker ist als die Oberflächenschicht. Eine mögliche Übergangsmatrix ist gegeben durch
 Damit die Sprungschicht auf lange Sicht dicker ist als die Oberflächenschicht muss ein erhöhten Zufluss in die Sprungschicht oder eine Verringerung des Abflusses aus der Sprungschicht vorliegen.
Damit die Sprungschicht auf lange Sicht dicker ist als die Oberflächenschicht muss ein erhöhten Zufluss in die Sprungschicht oder eine Verringerung des Abflusses aus der Sprungschicht vorliegen.
c)  Werte für
Werte für  bestimmen
Du hast folgende Übergangsmatrix gegeben:
bestimmen
Du hast folgende Übergangsmatrix gegeben:
 Du sollst den möglichen Bereich für
Du sollst den möglichen Bereich für  bestimmen. Diesen liest du am Besten aus dem Eintrag
bestimmen. Diesen liest du am Besten aus dem Eintrag  ab, da dieser zwischen 0 und 1 liegen muss. Das bedeutet, dass:
ab, da dieser zwischen 0 und 1 liegen muss. Das bedeutet, dass:
 und
und  Stelle diese beiden Gleichungen um. Du erhältst für
Stelle diese beiden Gleichungen um. Du erhältst für  den folgenden Bereich:
den folgenden Bereich:  .
.
 Matrix für stabile Verteilung
Bestimme eine Matrix
Matrix für stabile Verteilung
Bestimme eine Matrix  so, dass sich eine stabile Verteilung mit einer 1 m dicken Oberflächenschicht, einer 3 m dicken Sprungschicht und einer 5 m dicken Tiefenschicht ergibt. Der passende Ansatz ist gegeben durch:
so, dass sich eine stabile Verteilung mit einer 1 m dicken Oberflächenschicht, einer 3 m dicken Sprungschicht und einer 5 m dicken Tiefenschicht ergibt. Der passende Ansatz ist gegeben durch:
 Multipliziere die Matrix mit dem Vektor und du erhältst:
Multipliziere die Matrix mit dem Vektor und du erhältst:
 Das ergibt folgendes lineares Gleichungssystem:
Das ergibt folgendes lineares Gleichungssystem:
 Stelle Gleichung (1) nach
Stelle Gleichung (1) nach  um:
um:
 Stelle Gleichung (3) nach
Stelle Gleichung (3) nach  um:
um:
 Dann ergibt sich für
Dann ergibt sich für  .
Wähle
.
Wähle  geeignet, z.B.
geeignet, z.B.  . Dann gilt
. Dann gilt  und
und  . Die Übergangsmatrix hat dann folgende Form:
. Die Übergangsmatrix hat dann folgende Form:

a)  Übergangsgraph
Den Übergangsgraphen erhältst du, indem du jeder Schicht einen Knoten zuordnest. Durch Pfeile zwischen den entsprechenden Knoten, kannst du die Übergange zwischen den Schichten darstellen. Beschrifte die Pfeile jeweils mit der zugehörigen Übergangswahrscheinlichkeit aus der Tabelle.
Übergangsgraph
Den Übergangsgraphen erhältst du, indem du jeder Schicht einen Knoten zuordnest. Durch Pfeile zwischen den entsprechenden Knoten, kannst du die Übergange zwischen den Schichten darstellen. Beschrifte die Pfeile jeweils mit der zugehörigen Übergangswahrscheinlichkeit aus der Tabelle.
Dein Übergangsgraph sollte dann wie folgt aussehen:

 Mittlere Zeile im Sachzusammenhang erklären
Du sollst die Werte der mittleren Zeile im Sachzusammenhang erklären. Die Werte der Zeile geben an, dass pro Zeiteinheit
Mittlere Zeile im Sachzusammenhang erklären
Du sollst die Werte der mittleren Zeile im Sachzusammenhang erklären. Die Werte der Zeile geben an, dass pro Zeiteinheit  von der Dicke der Oberflächenschicht zur Dicke der Sprungschicht hinzukommen,
von der Dicke der Oberflächenschicht zur Dicke der Sprungschicht hinzukommen,  von der Dicke der Sprungschicht erhalten bleiben und
von der Dicke der Sprungschicht erhalten bleiben und  von der Dicke der Tiefenschicht zur Dicke der Sprungschicht hinzukommen.
von der Dicke der Tiefenschicht zur Dicke der Sprungschicht hinzukommen.
 Schichtdicke bestimmen
Zu Beginn ist jede der Schichten 3 m dick, du sollst die Schichtdicken nach fünf Zeiteinheiten berechnen. Die Übergangsmatrix
Schichtdicke bestimmen
Zu Beginn ist jede der Schichten 3 m dick, du sollst die Schichtdicken nach fünf Zeiteinheiten berechnen. Die Übergangsmatrix
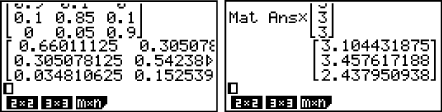
 gibt die Übergänge pro Zeiteinheit an, das bedeutet, dass du die Matrix 5 mal mit sich selbst multiplizieren musst, um die Verteilung pro 5 Zeiteinheiten zu erhalten. Dies kannst du mit deinem GTR tun. Eine Matrix kannst du im CALC-Menü unter
gibt die Übergänge pro Zeiteinheit an, das bedeutet, dass du die Matrix 5 mal mit sich selbst multiplizieren musst, um die Verteilung pro 5 Zeiteinheiten zu erhalten. Dies kannst du mit deinem GTR tun. Eine Matrix kannst du im CALC-Menü unter

 Nach fünf Zeiteinheiten beträgt die Dicke der Oberflächenschicht
Nach fünf Zeiteinheiten beträgt die Dicke der Oberflächenschicht  , die der Sprungschicht
, die der Sprungschicht  und die der Tiefenschicht
und die der Tiefenschicht  .
.
Dein Übergangsgraph sollte dann wie folgt aussehen:

F4: MATH  F1: MAT
F1: MAT
eingeben. Jetzt musst du noch die Schichtdicke von je 3 m beachten, diese also mit der Verteilung pro 5 Zeiteinheiten multiplizieren. Du erhältst dann für die Verteilung nach 5 Zeiteinheiten:

b)  Übergangsmatrix erstellen
Erstelle eine veränderte Übergangsmatrix so, dass die Sprungschicht auf lange Sicht dicker ist als die Oberflächenschicht. Eine mögliche Übergangsmatrix ist gegeben durch
Übergangsmatrix erstellen
Erstelle eine veränderte Übergangsmatrix so, dass die Sprungschicht auf lange Sicht dicker ist als die Oberflächenschicht. Eine mögliche Übergangsmatrix ist gegeben durch
 Damit die Sprungschicht auf lange Sicht dicker ist als die Oberflächenschicht muss ein erhöhten Zufluss in die Sprungschicht oder eine Verringerung des Abflusses aus der Sprungschicht vorliegen.
Damit die Sprungschicht auf lange Sicht dicker ist als die Oberflächenschicht muss ein erhöhten Zufluss in die Sprungschicht oder eine Verringerung des Abflusses aus der Sprungschicht vorliegen.
c)  Werte für
Werte für  bestimmen
Du hast folgende Übergangsmatrix gegeben:
bestimmen
Du hast folgende Übergangsmatrix gegeben:
 Du sollst den möglichen Bereich für
Du sollst den möglichen Bereich für  bestimmen. Diesen liest du am Besten aus dem Eintrag
bestimmen. Diesen liest du am Besten aus dem Eintrag  ab, da dieser zwischen 0 und 1 liegen muss. Das bedeutet, dass:
ab, da dieser zwischen 0 und 1 liegen muss. Das bedeutet, dass:
 und
und  Stelle diese beiden Gleichungen um. Du erhältst für
Stelle diese beiden Gleichungen um. Du erhältst für  den folgenden Bereich:
den folgenden Bereich:  .
.
 Matrix für stabile Verteilung
Bestimme eine Matrix
Matrix für stabile Verteilung
Bestimme eine Matrix  so, dass sich eine stabile Verteilung mit einer 1 m dicken Oberflächenschicht, einer 3 m dicken Sprungschicht und einer 5 m dicken Tiefenschicht ergibt. Der passende Ansatz ist gegeben durch:
so, dass sich eine stabile Verteilung mit einer 1 m dicken Oberflächenschicht, einer 3 m dicken Sprungschicht und einer 5 m dicken Tiefenschicht ergibt. Der passende Ansatz ist gegeben durch:
 Multipliziere die Matrix mit dem Vektor und du erhältst:
Multipliziere die Matrix mit dem Vektor und du erhältst:
 Das ergibt folgendes lineares Gleichungssystem:
Das ergibt folgendes lineares Gleichungssystem:
 Stelle Gleichung (1) nach
Stelle Gleichung (1) nach  um:
um:
 Stelle Gleichung (3) nach
Stelle Gleichung (3) nach  um:
um:
 Dann ergibt sich für
Dann ergibt sich für  .
Wähle
.
Wähle  geeignet, z.B.
geeignet, z.B.  . Dann gilt
. Dann gilt  und
und  . Die Übergangsmatrix hat dann folgende Form:
. Die Übergangsmatrix hat dann folgende Form:
